Kotak T mengandungi lima keping kad berlabel dengan huruf “C, E, L, I, K”. Dua keping kad dikeluarkan secara rawak dari kotak T satu demi satu tanpa pemulangan.
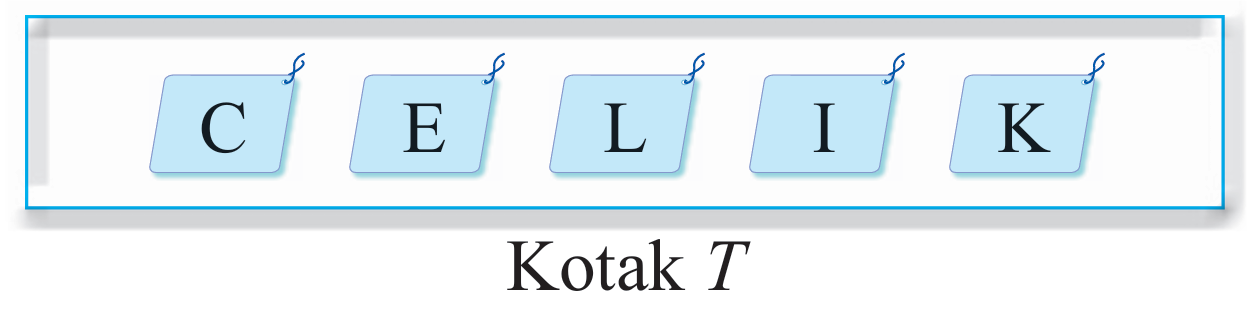
Hitung kebarangkalian mendapat kad pertama berhuruf konsonan dan kad kedua berhuruf vokal.
Penyelesaian:
$$ \begin{aligned} &\text { Ruang sampel dua keping kad dipilih }\\ &\begin{aligned} = & \{(\mathrm{C}, \mathrm{E}),(\mathrm{C}, \mathrm{~L}),(\mathrm{C}, \mathrm{I}),(\mathrm{C}, \mathrm{~K}), \\ & (\mathrm{E}, \mathrm{C}),(\mathrm{E}, \mathrm{~L}),(\mathrm{E}, \mathrm{I}),(\mathrm{E}, \mathrm{~K}), \\ & (\mathrm{L}, \mathrm{C}),(\mathrm{I}, \mathrm{E}),(\mathrm{L}, \mathrm{I}),(\mathrm{L}, \mathrm{~K}), \\ & (\mathrm{I}, \mathrm{C}),(\mathrm{I}, \mathrm{E}),(\mathrm{I}, \mathrm{~L}),(\mathrm{I}, \mathrm{~K}), \\ & (\mathrm{K}, \mathrm{C}),(\mathrm{K}, \mathrm{E}),(\mathrm{K}, \mathrm{~L}),(\mathrm{K}, \mathrm{I})\} \end{aligned} \end{aligned} $$
Ruang sampel kad pertama berhuruf konsonan dan kad kedua berhuruf vokal
= {(C, E), (C, I), (L, E), (L, I), (K, E), (K, I)}
$$
\begin{aligned}
& \text { P (kad pertama berhuruf konsonan dan } \\
& \text { kad kedua berhuruf vokal) } \\
& \quad=\frac{6}{20} \\
& \quad=\frac{3}{10}
\end{aligned}
$$

Sebuah kotak mengandungi dua belas biji mentol. Dalam kotak mentol itu, terdapat dua biji mentol yang telah terbakar. Dua biji mentol dipilih secara rawak dari kotak mentol. Dengan melakarkan gambar rajah pokok, hitung kebarangkalian mendapat kedua-dua biji mentol terbakar.
Penyelesaian:
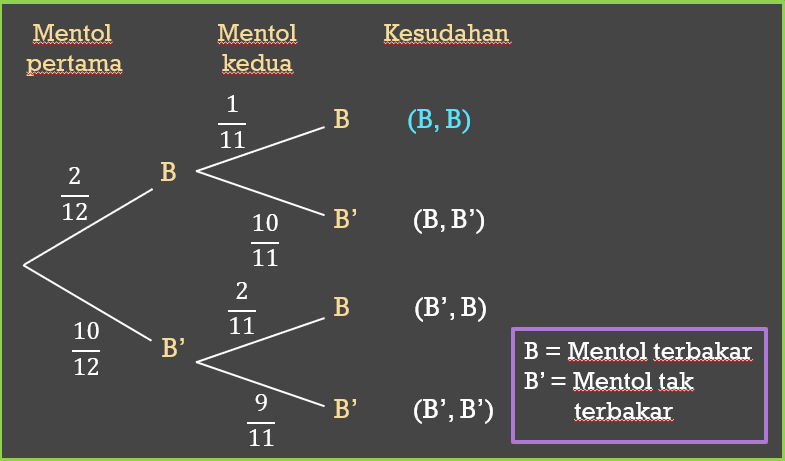
$$ \begin{aligned} & P(\text { kedua-dua biji mentol terbakar) } \\ & =P(B, B) \\ & =\frac{2}{12} \times \frac{1}{11} \\ & =\frac{2}{132} \\ & =\frac{1}{66} \end{aligned} $$
Jadual di bawah menunjukkan bilangan ahli Persatuan Sains dan Matematik di SMK Didik Jaya.
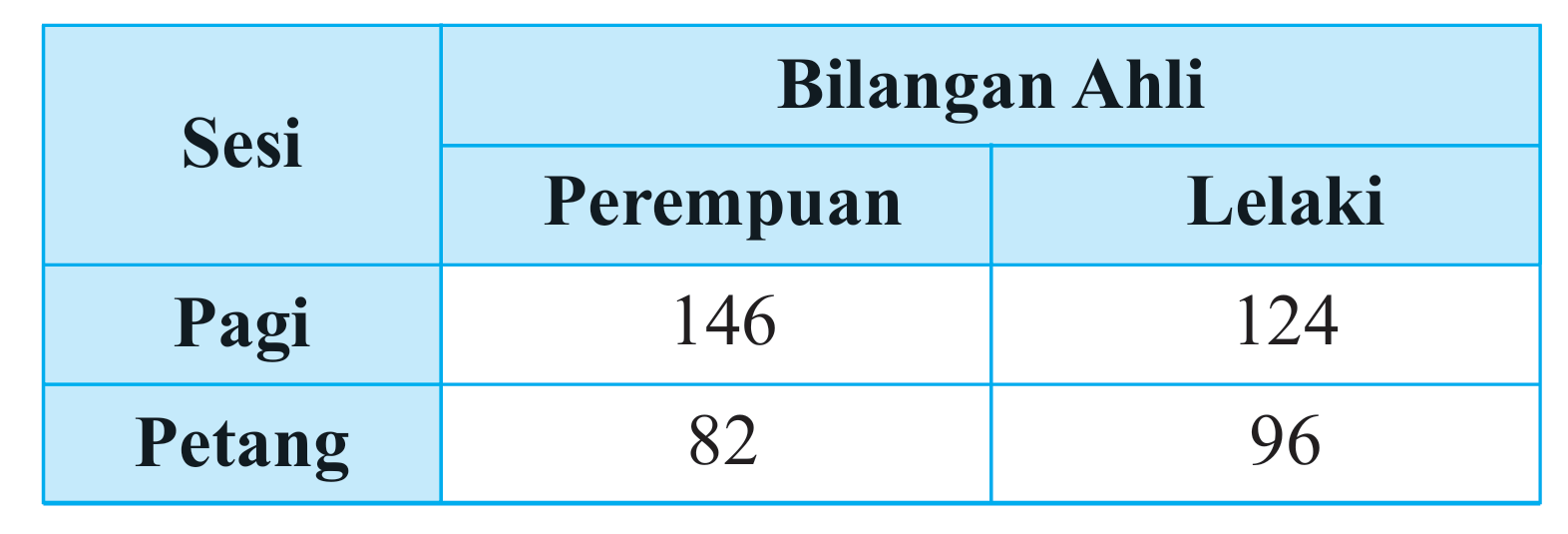
Dua orang ahli dipilih secara rawak
(a) daripada ahli lelaki, hitung kebarangkalian kedua-dua orang ahli dipilih ialah murid sesi pagi (berikan jawapan anda betul kepada empat angka bererti).
(b) daripada sesi petang, hitung kebarangkalian kedua-dua orang murid dipilih ialah perempuan (berikan jawapan anda betul kepada empat angka bererti).
Penyelesaian:
(a)
$$ \begin{aligned} & \text { Jumlah ahli lelaki }=124+96=220 \text { orang } \\ & P \text { (kedua-dua orang ahli ialah murid sesi pagi) } \\ & =\frac{124}{220} \times \frac{123}{219} \\ & =0.3166 \end{aligned} $$
Read morePraktis Kendiri 9.2c (Soalan 4 – 6) – Buku Teks Matematik Tingkatan 4 Bab 9