Soalan 3:
Tujuh keping kad berlabel dengan huruf “B, A, H, A, G, I, A” dimasukkan ke dalam sebuah kotak. Sekeping kad dipilih secara rawak.
L ialah peristiwa mendapat kad berhuruf vokal.
M ialah peristiwa mendapat kad berhuruf konsonan.
N ialah peristiwa mendapat kad berhuruf “B”.
(a) Lukis satu gambar rajah Venn untuk mewakili hubungan antara peristiwa L, M dan N di atas.
(b) Tentu sahkan rumus penambahan kebarangkalian bagi setiap peristiwa bergabung berikut dengan menyenaraikan semua kesudahan yang mungkin.
(i) P(L atau M)
(ii) P(L atau N)
(iii) P(M atau N)
Penyelesaian:
(a)
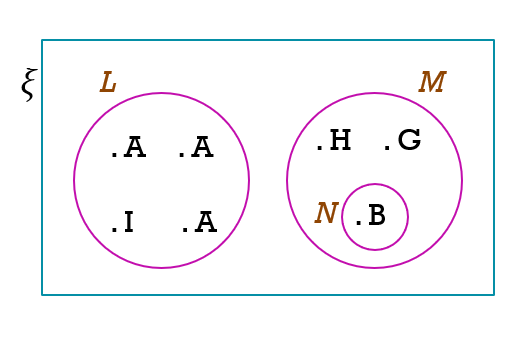
(b)(i)
$$ \begin{aligned} & L \cap M=\{ \}, \\ & P(L)+P(M)=\frac{4}{7}+\frac{3}{7} \\ &=\frac{7}{7} \\ &=1 \end{aligned} $$
$$ \begin{aligned} & L=\{\mathrm{A}, \mathrm{~A}, \mathrm{I}, \mathrm{~A}\}, M=\{\mathrm{B}, \mathrm{H}, \mathrm{G}\} \\ & L \cup M=\{\mathrm{A}, \mathrm{~A}, \mathrm{I}, \mathrm{~A}, \mathrm{~B}, \mathrm{H}, \mathrm{G}\} \\ & \begin{array}{l} P(L \cup M)=\frac{7}{7} \\ \quad=1 \end{array} \end{aligned} $$
$$ \text { Maka, terbukti } P(\mathbf{L})+P(\mathbf{M})=P(\mathbf{L} \cup \mathbf{M}) \text {. } $$
(b)(ii)
$$ \begin{aligned} & L \cap N=\{ \}, \\ & P(L)+P(N)=\frac{4}{7}+\frac{1}{7} \\ &=\frac{5}{7} \end{aligned} $$
$$ \begin{aligned} & L=\{\mathrm{A}, \mathrm{~A}, \mathrm{I}, \mathrm{~A}\}, N=\{\mathrm{B}\} \\ & L \cup N=\{\mathrm{A}, \mathrm{~A}, \mathrm{I}, \mathrm{~A}, \mathrm{~B}\} \\ & P(L \cup N)=\frac{5}{7} \end{aligned} $$
$$ \text { Maka, terbukti } P(\mathrm{~L})+P(\mathrm{~N})=P(\mathrm{~L} \cup \mathrm{~N}) \text {. } $$
(b)(iii)
$$ \begin{aligned} & M \cap N=\{B\}, \\ & P(M)+P(N)-P(M \cap N)=\frac{3}{7}+\frac{1}{7}-\frac{1}{7} \\ &=\frac{3}{7} \end{aligned} $$
$$ \begin{aligned} & M=\{\mathrm{B}, \mathrm{H}, \mathrm{G}\}, N=\{\mathrm{B}\} \\ & M \cup N=\{\mathrm{B}, \mathrm{H}, \mathrm{G}\} \\ & P(M \cup N)=\frac{3}{7} \end{aligned} $$
$$ \text { Maka, terbukti } P(\mathrm{M})+P(\mathrm{~N})-P(\mathrm{M} \cap \mathrm{~N})=P(\mathrm{M} \cup \mathrm{~N}) \text {. } $$
Tujuh keping kad berlabel dengan huruf “B, A, H, A, G, I, A” dimasukkan ke dalam sebuah kotak. Sekeping kad dipilih secara rawak.
L ialah peristiwa mendapat kad berhuruf vokal.
M ialah peristiwa mendapat kad berhuruf konsonan.
N ialah peristiwa mendapat kad berhuruf “B”.
(a) Lukis satu gambar rajah Venn untuk mewakili hubungan antara peristiwa L, M dan N di atas.
(b) Tentu sahkan rumus penambahan kebarangkalian bagi setiap peristiwa bergabung berikut dengan menyenaraikan semua kesudahan yang mungkin.
(i) P(L atau M)
(ii) P(L atau N)
(iii) P(M atau N)
Penyelesaian:
(a)

(b)(i)
$$ \begin{aligned} & L \cap M=\{ \}, \\ & P(L)+P(M)=\frac{4}{7}+\frac{3}{7} \\ &=\frac{7}{7} \\ &=1 \end{aligned} $$
$$ \begin{aligned} & L=\{\mathrm{A}, \mathrm{~A}, \mathrm{I}, \mathrm{~A}\}, M=\{\mathrm{B}, \mathrm{H}, \mathrm{G}\} \\ & L \cup M=\{\mathrm{A}, \mathrm{~A}, \mathrm{I}, \mathrm{~A}, \mathrm{~B}, \mathrm{H}, \mathrm{G}\} \\ & \begin{array}{l} P(L \cup M)=\frac{7}{7} \\ \quad=1 \end{array} \end{aligned} $$
$$ \text { Maka, terbukti } P(\mathbf{L})+P(\mathbf{M})=P(\mathbf{L} \cup \mathbf{M}) \text {. } $$
(b)(ii)
$$ \begin{aligned} & L \cap N=\{ \}, \\ & P(L)+P(N)=\frac{4}{7}+\frac{1}{7} \\ &=\frac{5}{7} \end{aligned} $$
$$ \begin{aligned} & L=\{\mathrm{A}, \mathrm{~A}, \mathrm{I}, \mathrm{~A}\}, N=\{\mathrm{B}\} \\ & L \cup N=\{\mathrm{A}, \mathrm{~A}, \mathrm{I}, \mathrm{~A}, \mathrm{~B}\} \\ & P(L \cup N)=\frac{5}{7} \end{aligned} $$
$$ \text { Maka, terbukti } P(\mathrm{~L})+P(\mathrm{~N})=P(\mathrm{~L} \cup \mathrm{~N}) \text {. } $$
(b)(iii)
$$ \begin{aligned} & M \cap N=\{B\}, \\ & P(M)+P(N)-P(M \cap N)=\frac{3}{7}+\frac{1}{7}-\frac{1}{7} \\ &=\frac{3}{7} \end{aligned} $$
$$ \begin{aligned} & M=\{\mathrm{B}, \mathrm{H}, \mathrm{G}\}, N=\{\mathrm{B}\} \\ & M \cup N=\{\mathrm{B}, \mathrm{H}, \mathrm{G}\} \\ & P(M \cup N)=\frac{3}{7} \end{aligned} $$
$$ \text { Maka, terbukti } P(\mathrm{M})+P(\mathrm{~N})-P(\mathrm{M} \cap \mathrm{~N})=P(\mathrm{M} \cup \mathrm{~N}) \text {. } $$