Soalan 1:
Tujuh keping kad yang berlabel dengan huruf “G, E, M, B, I, R, A” dimasukkan ke dalam sebuah kotak. Sekeping kad dipilih secara rawak dari kotak.
Dengan menyenaraikan semua kesudahan yang mungkin, hitung kebarangkalian kad yang dipilih berlabel huruf vokal atau “R”.
Penyelesaian:
Kad yang berlabel huruf vokal = {E, I, A}
Kad yang berlabel huruf “R” = {R}
$$ \begin{aligned} P(\text { Kad yang berlabel huruf vokal atau ‘R”‘ }) & =\{E, I, A, R\} \\ & =\frac{4}{7} \end{aligned} $$
Tujuh keping kad yang berlabel dengan huruf “G, E, M, B, I, R, A” dimasukkan ke dalam sebuah kotak. Sekeping kad dipilih secara rawak dari kotak.
Dengan menyenaraikan semua kesudahan yang mungkin, hitung kebarangkalian kad yang dipilih berlabel huruf vokal atau “R”.Penyelesaian:
Kad yang berlabel huruf vokal = {E, I, A}
Kad yang berlabel huruf “R” = {R}
$$ \begin{aligned} P(\text { Kad yang berlabel huruf vokal atau ‘R”‘ }) & =\{E, I, A, R\} \\ & =\frac{4}{7} \end{aligned} $$
Soalan 2:
Dua kotak yang berlabel K dan L masing-masing mengandungi empat keping kad berlabel dengan huruf “S, E, R, I” dan tiga keping kad berlabel dengan nombor “4, 5, 6”. Sekeping kad dipilih secara rawak dari kotak K dan L masing-masing.
Dengan menyenaraikan semua kesudahan yang mungkin, hitung kebarangkalian mendapat huruf “S” dari kotak K atau nombor gandaan 3 dari kotak L.
Penyelesaian:
Ruang sampel sekeping kad dipilih secara rawak dari kotak K dan kotak L
= {(S, 4), (S, 5), (S, 6), (E, 4), (E, 5), (E, 6), (R, 4), (R, 5), (R, 6), (I, 4), (I, 5), (I, 6)}
Ruang sampel mendapat huruf “S” dari kotak K atau gandaan 3 dari kotak L $$ \begin{aligned} & =\{(\mathrm{S}, 4),(\mathrm{S}, 5),(\mathrm{S}, 6),(\mathrm{E}, 6),(\mathrm{R}, 6),(\mathrm{I}, 6)\} \\ & =\frac{6}{12} \\ & =\frac{1}{2} \end{aligned} $$
Dua kotak yang berlabel K dan L masing-masing mengandungi empat keping kad berlabel dengan huruf “S, E, R, I” dan tiga keping kad berlabel dengan nombor “4, 5, 6”. Sekeping kad dipilih secara rawak dari kotak K dan L masing-masing.
Dengan menyenaraikan semua kesudahan yang mungkin, hitung kebarangkalian mendapat huruf “S” dari kotak K atau nombor gandaan 3 dari kotak L.
Penyelesaian:
Ruang sampel sekeping kad dipilih secara rawak dari kotak K dan kotak L
= {(S, 4), (S, 5), (S, 6), (E, 4), (E, 5), (E, 6), (R, 4), (R, 5), (R, 6), (I, 4), (I, 5), (I, 6)}
Ruang sampel mendapat huruf “S” dari kotak K atau gandaan 3 dari kotak L $$ \begin{aligned} & =\{(\mathrm{S}, 4),(\mathrm{S}, 5),(\mathrm{S}, 6),(\mathrm{E}, 6),(\mathrm{R}, 6),(\mathrm{I}, 6)\} \\ & =\frac{6}{12} \\ & =\frac{1}{2} \end{aligned} $$
Soalan 3:
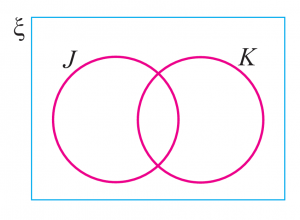
Kebarangkalian Jessie dilantik sebagai pengerusi Kelab Kewangan (J) dan ketua rumah sukan (K) masing-masing ialah 3/8 dan 2/9.
(a) Lengkapkan gambar rajah Venn di sebelah untuk mewakili hubungan kebarangkalian Jessie dilantik sebagai pengerusi Kelab Kewangan dan ketua rumah sukan.
(b) Hitung kebarangkalian Jessie tidak dilantik sebagai pengerusi Kelab Kewangan atau ketua rumah sukan.
Penyelesaian:
(a)
P(Jessie dilantik sebagai pengerusi Kelab Kewangan dan ketua rumah sukan)
$$ \begin{aligned} & =\frac{3}{8} \times \frac{2}{9} \\ & =\frac{1}{12} \end{aligned} $$
P(Jessie hanya dilantik sebagai ketua rumah sukan)
$$ \begin{aligned} & =\frac{2}{9}-\frac{1}{12} \\ & =\frac{5}{36} \end{aligned} $$
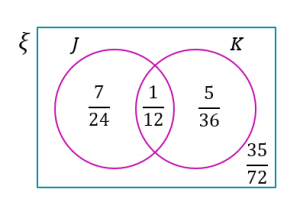
(b)
P(Jessie tidak dilantik sebagai pengerusi Kelab Kewangan atau ketua rumah sukan)
$$ \begin{aligned} & =1-\left(\frac{7}{24}+\frac{5}{36}+\frac{1}{12}\right) \\ & =\frac{35}{72} \end{aligned} $$
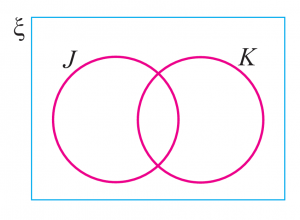
Kebarangkalian Jessie dilantik sebagai pengerusi Kelab Kewangan (J) dan ketua rumah sukan (K) masing-masing ialah 3/8 dan 2/9.
(a) Lengkapkan gambar rajah Venn di sebelah untuk mewakili hubungan kebarangkalian Jessie dilantik sebagai pengerusi Kelab Kewangan dan ketua rumah sukan.
(b) Hitung kebarangkalian Jessie tidak dilantik sebagai pengerusi Kelab Kewangan atau ketua rumah sukan.
Penyelesaian:
(a)
P(Jessie dilantik sebagai pengerusi Kelab Kewangan dan ketua rumah sukan)
$$ \begin{aligned} & =\frac{3}{8} \times \frac{2}{9} \\ & =\frac{1}{12} \end{aligned} $$
P(Jessie hanya dilantik sebagai pengerusi Kelab Kewangan)
$$
\begin{aligned}
& =\frac{3}{8}-\frac{1}{12} \\
& =\frac{7}{24}
\end{aligned}
$$
P(Jessie hanya dilantik sebagai ketua rumah sukan)
$$ \begin{aligned} & =\frac{2}{9}-\frac{1}{12} \\ & =\frac{5}{36} \end{aligned} $$
(b)
P(Jessie tidak dilantik sebagai pengerusi Kelab Kewangan atau ketua rumah sukan)
$$ \begin{aligned} & =1-\left(\frac{7}{24}+\frac{5}{36}+\frac{1}{12}\right) \\ & =\frac{35}{72} \end{aligned} $$
Soalan 4:
Persatuan Geografi SMK Cerdik mengadakan rombongan lawatan sambil belajar ke Kota Kinabalu. Kebarangkalian Mandy dan Geetha menyertai rombongan ini masing-masing ialah 4/7 dan 9/14. Lengkapkan gambar rajah pokok di bawah. Seterusnya, hitung kebarangkalian hanya seorang daripada Mandy atau Geetha menyertai rombongan ini.
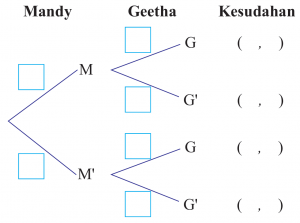
Penyelesaian:
$$ P(\text { Mandy tidak menyertai rombongan })=\frac{3}{7} $$
$$ P(\text { Geetha tidak menyertai rombongan })=\frac{5}{14} $$
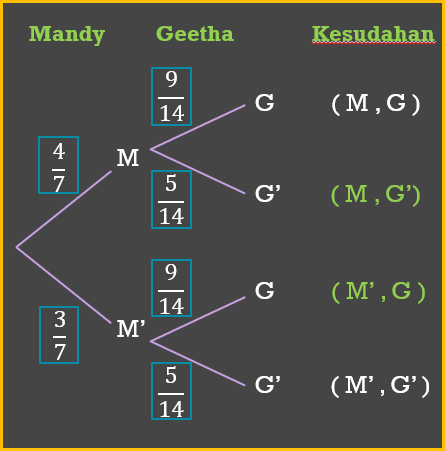
$$ \begin{aligned} & P(\text { Mandy atau Geetha menyertai rombongan }) \\ & =\left(\mathrm{M}, \mathrm{G}^{\prime}\right)+\left(\mathrm{M}^{\prime}, \mathrm{G}\right) \\ & =\left(\frac{4}{7} \times \frac{5}{14}\right)+\left(\frac{3}{7} \times \frac{9}{14}\right) \\ & =\frac{47}{98} \end{aligned} $$
Persatuan Geografi SMK Cerdik mengadakan rombongan lawatan sambil belajar ke Kota Kinabalu. Kebarangkalian Mandy dan Geetha menyertai rombongan ini masing-masing ialah 4/7 dan 9/14. Lengkapkan gambar rajah pokok di bawah. Seterusnya, hitung kebarangkalian hanya seorang daripada Mandy atau Geetha menyertai rombongan ini.
Penyelesaian:
$$ P(\text { Mandy tidak menyertai rombongan })=\frac{3}{7} $$
$$ P(\text { Geetha tidak menyertai rombongan })=\frac{5}{14} $$
$$ \begin{aligned} & P(\text { Mandy atau Geetha menyertai rombongan }) \\ & =\left(\mathrm{M}, \mathrm{G}^{\prime}\right)+\left(\mathrm{M}^{\prime}, \mathrm{G}\right) \\ & =\left(\frac{4}{7} \times \frac{5}{14}\right)+\left(\frac{3}{7} \times \frac{9}{14}\right) \\ & =\frac{47}{98} \end{aligned} $$