Kebarangkalian Peristiwa Bergabung

9.5.4 Kebarangkalian Peristiwa Bergabung, SPM Praktis (Kertas 2)

Soalan 7:Rajah bawah menunjukkan 4 keping kad berlabel dengan huruf.Dua keping kad dipilih secara rawak daripada kotak itu, satu demi satu, tanpa dikembalikan.(a) Senaraikan ruang sampel.(b) Carikan kebarangkalian bahawa(i) sekurung-kurungnya satu kad yang dipilih berlabel C,(ii) kedua-dua kad yang dipilih berlabel dengan huruf yang sama. Jawapan dan penyelesaian:(a)Ruang sampel, S= {(C, O1), (C, O2), (C, … Read more

9.5.3 Kebarangkalian Peristiwa Bergabung, SPM Praktis (Kertas 2)

Soalan 5:Satu dadu yang adil dilambung. Kemudian sekeping kad dipilih secara rawak dari sebuah kotak yang mengandungi sekeping kad kuning, sekeping kad merah dan sekeping kad ungu. (a) Dengan menggunakan huruf Y untuk mewakili kad kuning, huruf R untuk menwakili kad merah dan huruf P untuk mewakili kad ungu, lengkapkan ruang sampel pada ruang jawapan. … Read more

9.5.2 Kebarangkalian Peristiwa Bergabung, SPM Praktis (Kertas 2)

9.5.2 Kebarangkalian Peristiwa Bergabung, SPM Praktis (Kertas 2) Soalan 3: Rajah di bawah menunjukkan dua kad huruf dalam kotak A dan tiga kad nombor di dalam kotak B. Satu kad dipilih secara rawak daripada kotak A dan kemudian satu kad pula dipilih secara rawak daripada kotak B. Dengan menyenaraikan sampel bagi semua kesudahan peristiwa yang … Read more

9.5.1 Kebarangkalian Peristiwa Bergabung, SPM Praktis (Kertas 2)

9.5.1 Kebarangkalian Peristiwa Bergabung, SPM Praktis (Kertas 2) Soalan 1: Tiga belas keping kad huruf seperti yang ditunjukkan dalam rajah di atas dimasukkan ke dalam sebuah kotak. Dua keping kad dikeluarkan secara rawak daripada kotak itu, satu demi satu, tanpa pengembalian. Hitung kebarangkalian bahawa (a) kad pertama yang dikeluarkan ialah kad huruf Ndan kad kedua … Read more

9.4.2 Kebarangkalian Peristiwa Bergabung, SPM Praktis (Kertas 1)

Soalan 5:Dalam sebuah syarikat, seramai 300 orang pekerja menaiki bas, 60 orang pekerja menaiki kereta dan selebihnya menunggang motosikal ke tempat kerja. Seorang pekerja dipilih secara rawak. Kebarangkalian memilih seorang pekerja yang menaiki bas ke tempat kerja ialah ⅔. Cari kebarangkalian memilih seorang pekerja yang tidak menunggang motosikal untuk ke tempat kerja itu. Penyelesaian: Katakan y ialah bilangan pekerja menunggang motosikal ke tempat kerja. … Read more

9.4.1 Kebarangkalian Peristiwa Bergabung, SPM Praktis (Kertas 1)

9.4.1 Kebarangkalian Peristiwa Bergabung, SPM Praktis (Kertas 1) Soalan 1: Sebuah beg mengandungi 36 biji guli yang berwarna hitam dan putih. Diberi bahawa kebarangkalian sebiji guli hitam dipilih daripada beg ialah 5 9 . Hitung bilangan guli putih perlu diambil keluar daripada beg supaya kebarangkalian sebiji guli hitam dipilih ialah 5 8 . Penyelesaian: Bilangan … Read more

Praktis Komprehensif 9 (Soalan 9 – 11) – Buku Teks Matematik Tingkatan 4 Bab 9


Soalan 9:
Jacky mempunyai lapan helai baju kemeja dan tiga daripadanya berwarna biru. 40% daripada baju kemeja yang dimiliki oleh Halim berwarna biru. 1/5 daripada baju kemeja yang dimiliki oleh Kumar berwarna biru. Jacky, Halim dan Kumar masing-masing memilih sehelai baju kemeja untuk menghadiri satu mesyuarat secara rawak. Hitung kebarangkalian bahawa dua orang daripada mereka akan memakai baju kemeja berwarna biru.

Penyelesaian:
$$ \begin{aligned} & P(\text { Jacky biru })=\frac{3}{8}, P(\text { Jacky bukan biru })=\frac{5}{8} \\ & P(\text { Halim biru })=\frac{2}{5}, P(\text { Halim bukan biru })=\frac{3}{5} \\ & P(\text { Kumar biru })=\frac{1}{5}, P(\text { Kumar bukan biru })=\frac{4}{5} \end{aligned} $$

$$ \begin{aligned} &\text { Kebarangkalian dua orang memakai baju biru }\\ &\begin{aligned} & =P(J b, H b, K b b)+P(J b, H b b, K b)+P(J b b, H b, K b) \\ & =\left(\frac{3}{8} \times \frac{2}{5} \times \frac{4}{5}\right)+\left(\frac{3}{8} \times \frac{3}{5} \times \frac{1}{5}\right)+\left(\frac{5}{8} \times \frac{2}{5} \times \frac{1}{5}\right) \\ & =\frac{3}{25}+\frac{9}{200}+\frac{1}{20} \\ & =\frac{43}{200} \end{aligned} \end{aligned} $$

Read morePraktis Komprehensif 9 (Soalan 9 – 11) – Buku Teks Matematik Tingkatan 4 Bab 9

Praktis Komprehensif 9 (Soalan 5 – 8) – Buku Teks Matematik Tingkatan 4 Bab 9


Soalan 5:
Kebarangkalian Kam Seng lulus dalam mata pelajaran Fizik dan Kimia masing-masing ialah 0.58 dan 0.42. Hitung kebarangkalian bahawa
(a) Kam Seng lulus kedua-dua mata pelajaran,
(b) Kam Seng hanya lulus satu mata pelajaran.

Penyelesaian:
(a)
$$ \begin{array}{r} \text { Diberi } P(\text { Lulus Fizik })=0.58 \\ P(\text { Lulus Kimia })=0.42 \end{array} $$
$$ \begin{aligned} \text { Maka } P(\text { Lulus Fizik dan kimia }) & =0.58 \times 0.42 \\ & =0.2436 \end{aligned} $$


(b)
$$ \begin{aligned} & P(\text { Gagal Fizik })=1-0.58=0.42 \\ & P(\text { Gagal Kimia })=1-0.42=0.58 \end{aligned} $$
$$ \begin{aligned} & \text { Maka } P \text { (Iulus satu mata pelaiaran) } \\ & =P(\text { Lulus Fizik, Gagal Kimia) }+P(\text { Lulus Kimia, Gagal Fizik }) \\ & =(0.58 \times 0.58)+(0.42 \times 0.42) \\ & =0.5128 \end{aligned} $$


Soalan 6:
Fatimah menghantar surat permohonan kerja ke tiga buah syarikat. Kebarangkalian Fatimah mendapat penawaran daripada syarikat X, Y dan Z masing-masing ialah 3/5 , 4/9 dan 5/12 . Hitung kebarangkalian Fatimah mendapat penawaran daripada
(a) mana-mana dua syarikat,
(b) sekurang-kurangnya satu syarikat.

Penyelesaian:



(a)
$$ \begin{aligned} P & (\text { Tawaran daripada } 2 \text { syarikat }) \\ = & P(X Y Z)+P\left(X Y^{\prime} Z\right)+P\left(X^{\prime} Y Z\right) \\ = & \left(\frac{3}{5} \times \frac{4}{9} \times \frac{7}{12}\right)+\left(\frac{3}{5} \times \frac{5}{9} \times \frac{5}{12}\right) \\ & +\left(\frac{2}{5} \times \frac{4}{9} \times \frac{5}{12}\right) \\ = & \frac{7}{45}+\frac{5}{36}+\frac{2}{27} \\ = & \frac{199}{540} \end{aligned} $$


(b)
$$ \begin{aligned} & P(\text { Sekurang-kurang } 1 \text { syarikat }) \\ & =1-P\left(X^{\prime} Y^{\prime} Z^{\prime}\right) \\ & =1-\left(\frac{2}{5} \times \frac{5}{9} \times \frac{7}{12}\right) \\ & =\frac{47}{54} \end{aligned} $$


Soalan 7:
Diberi peristiwa A dan B ialah dua peristiwa yang saling eksklusif dan P(A) = 1/3,
(a) nyatakan nilai maksimum P(B).
(b) jika P(A B) = 7/9, kenal pasti P(B).

Penyelesaian:
(a)
$$ \begin{aligned} & \text { Nilai maksimum } P(B) \\ & =1-P(A) \\ & =1-\frac{1}{3} \\ & =\frac{2}{3} \end{aligned} $$


(b)
$$ \begin{aligned} & \text { Diberi } P(A \cup B)=\frac{7}{9} \\ & \begin{aligned} & P(A)+P(B)-P(A \cap B)=\frac{7}{9} \\ & \frac{1}{3}+P(B)-0=\frac{7}{9} \\ & P(B)=\frac{7}{9}-\frac{1}{3} \\ &=\frac{4}{9} \end{aligned} \end{aligned} $$


Soalan 8:
Kotak R mengandungi lima biji guli merah dan tujuh biji guli hijau manakala kotak T mengandungi empat biji guli merah dan lapan biji guli hijau. Sebiji guli dipilih secara rawak dari kotak R. Sekiranya guli itu berwarna merah, guli itu akan dimasukkan ke dalam kotak T. Sekiranya guli itu berwarna hijau, guli itu akan dikembalikan ke dalam kotak R. Seterusnya sebiji guli akan dipilih secara rawak dari kotak T. Warna guli yang dipilih akan dicatat.

(a) Hitung kebarangkalian
(i) kedua-dua biji guli yang dipilih berwarna merah,
(ii) kedua-dua biji guli yang dipilih berlainan warna.

(b) Kelas 4 Amanah mempunyai 36 orang murid. Sekiranya setiap murid daripada 4 Amanah diberi peluang memilih dua biji guli dengan keadaan seperti yang dinyatakan dan murid yang berjaya memilih dua biji guli yang berwarna hijau akan diberi hadiah bernilai RM5, anggarkan kos hadiah yang diperlukan.


Penyelesaian:
$$ \begin{aligned} &\text { Pada Kotak } R \text {, }\\ &P(M)=\frac{5}{12}, P(H)=\frac{7}{12} \end{aligned} $$
$$ \begin{aligned} &\text { Pada Kotak T, }\\ &P(M)=\frac{4}{12}, P(H)=\frac{8}{12} \end{aligned} $$

Read morePraktis Komprehensif 9 (Soalan 5 – 8) – Buku Teks Matematik Tingkatan 4 Bab 9

Praktis Komprehensif 9 (Soalan 1 – 4) – Buku Teks Matematik Tingkatan 4 Bab 9


Soalan 1:
Terdapat tiga batang pensel berwarna ungu dan dua batang pensel berwarna  hijau dalam sebuah kotak. Dua batang  pensel berwarna dipilih secara rawak  dari kotak satu demi satu tanpa pemulangan. Tulis ruang sampel bagi pensel warna dipilih.

Penyelesaian:
Batang pensel berwarna ungu = U
Batang pensel berwarna hijau = H
$$ \begin{aligned} &\text { Ruang sampel dua batang pensel berwarna dipilih }\\ &\begin{aligned} = & \left\{\left(\mathrm{U}_1, \mathrm{U}_2\right),\left(\mathrm{U}_1, \mathrm{U}_3\right),\left(\mathrm{U}_1, \mathrm{H}_1\right),\left(\mathrm{U}_1, \mathrm{H}_2\right),\left(\mathrm{U}_2, \mathrm{U}_1\right),\left(\mathrm{U}_2, \mathrm{U}_3\right),\right. \\ & \left(\mathrm{U}_2, \mathrm{H}_1\right),\left(\mathrm{U}_2, \mathrm{H}_2\right),\left(\mathrm{U}_3, \mathrm{U}_1\right),\left(\mathrm{U}_3, \mathrm{U}_2\right),\left(\mathrm{U}_3, \mathrm{H}_1\right),\left(\mathrm{U}_3, \mathrm{H}_2\right), \\ & \left(\mathrm{H}_1, \mathrm{U}_1\right),\left(\mathrm{H}_1, \mathrm{U}_2\right),\left(\mathrm{H}_1, \mathrm{U}_3\right),\left(\mathrm{H}_1, \mathrm{H}_2\right),\left(\mathrm{H}_2, \mathrm{U}_1\right),\left(\mathrm{H}_2, \mathrm{U}_2\right), \\ & \left.\left(\mathrm{H}_2, \mathrm{U}_3\right),\left(\mathrm{H}_2, \mathrm{H}_1\right)\right\} \end{aligned} \end{aligned} $$


Soalan 2:
Satu nombor dipilih secara rawak dari set S = {x: x ialah integer, 1 ≤ x ≤ 30}. Hitung kebarangkalian
(a)mendapat  nombor  gandaan 3 dan nombor gandaan 12.
(b) mendapat  nombor  faktor bagi 20 atau nombor faktor bagi 8.

Penyelesaian:
(a)
Nombor gandaan bagi 3 = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}
Nombor gandaan bagi 12 = {12, 24}
$$ \begin{aligned} P(\text { Gandaan bagi } 3 \text { dan } 12) & =\frac{2}{30} \\ & =\frac{1}{15} \end{aligned} $$


(b)
Nombor faktor bagi 20 = {1, 2, 4, 5, 10, 20}
Nombor faktor bagi 8 = {1, 2, 4, 8}
Nombor faktor bagi 8 atau 20 = {1, 2, 4, 5, 8, 10, 20}
$$ \therefore P(\text { Faktor bagi } 20 \text { atau } 8)=\frac{7}{30} $$


Soalan 3:
Dua keping kad berlabel dengan nombor “77, 91” dimasukkan dalam kotak M dan tiga keping kad berlabel dengan huruf “R, I, A” dimasukkan dalam kotak N. Sekeping kad dipilih secara rawak dari kotak M dan N masing-masing.

(a) Lengkapkan jadual berikut dengan semua kesudahan yang mungkin.


(b) Dengan menyenaraikan semua kesudahan yang mungkin, hitung kebarangkalian bahawa
(i) kad nombor dengan hasil tambah digit melebihi 10 dan kad konsonan dipilih.
(ii) kad nombor dengan hasil tambah digit melebihi 10 atau kad konsonan dipilih.


Penyelesaian:
(a)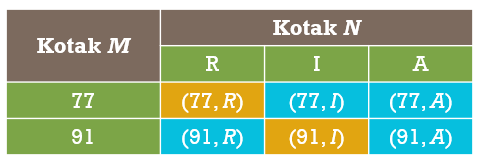

(b)(i)
Kad  nombor  dengan  hasil  tambah digit melebihi 10 dan kad konsonan = {(77, R)}
$$ \begin{aligned} &\text { P (hasil tambah digit melebihi } 10 \text { dan kad konsonan) }\\ &=\frac{1}{6} \end{aligned} $$

Read morePraktis Komprehensif 9 (Soalan 1 – 4) – Buku Teks Matematik Tingkatan 4 Bab 9

Praktis Kendiri 9.4a – Buku Teks Matematik Tingkatan 4 Bab 9

Soalan 1:Kajian tentang jantina anak terhadap 16 000 keluarga yang mempunyai dua orang anak telah dijalankan. Anggarkan bilangan keluarga yang mempunyai sekurang-kurangnya seorang anak lelaki dalam kajian tersebut.Penyelesaian:\begin{aligned} P(L, L)+P(L, P)+P(P, L) & =\left(\frac{1}{2} \times \frac{1}{2}\right)+\left(\frac{1}{2} \times \frac{1}{2}\right)+\left(\frac{1}{2} \times \frac{1}{2}\right) \\ & =\frac{3}{4} \end{aligned}$$ \begin{aligned} &\text { Maka, bilangan keluarga sekurang-kurangnya mempunyai seorang anak lelaki … Read more