Soalan 9:
Jacky mempunyai lapan helai baju kemeja dan tiga daripadanya berwarna biru. 40% daripada baju kemeja yang dimiliki oleh Halim berwarna biru. 1/5 daripada baju kemeja yang dimiliki oleh Kumar berwarna biru. Jacky, Halim dan Kumar masing-masing memilih sehelai baju kemeja untuk menghadiri satu mesyuarat secara rawak. Hitung kebarangkalian bahawa dua orang daripada mereka akan memakai baju kemeja berwarna biru.
Penyelesaian:
$$ \begin{aligned} & P(\text { Jacky biru })=\frac{3}{8}, P(\text { Jacky bukan biru })=\frac{5}{8} \\ & P(\text { Halim biru })=\frac{2}{5}, P(\text { Halim bukan biru })=\frac{3}{5} \\ & P(\text { Kumar biru })=\frac{1}{5}, P(\text { Kumar bukan biru })=\frac{4}{5} \end{aligned} $$
$$ \begin{aligned} &\text { Kebarangkalian dua orang memakai baju biru }\\ &\begin{aligned} & =P(J b, H b, K b b)+P(J b, H b b, K b)+P(J b b, H b, K b) \\ & =\left(\frac{3}{8} \times \frac{2}{5} \times \frac{4}{5}\right)+\left(\frac{3}{8} \times \frac{3}{5} \times \frac{1}{5}\right)+\left(\frac{5}{8} \times \frac{2}{5} \times \frac{1}{5}\right) \\ & =\frac{3}{25}+\frac{9}{200}+\frac{1}{20} \\ & =\frac{43}{200} \end{aligned} \end{aligned} $$
Jacky mempunyai lapan helai baju kemeja dan tiga daripadanya berwarna biru. 40% daripada baju kemeja yang dimiliki oleh Halim berwarna biru. 1/5 daripada baju kemeja yang dimiliki oleh Kumar berwarna biru. Jacky, Halim dan Kumar masing-masing memilih sehelai baju kemeja untuk menghadiri satu mesyuarat secara rawak. Hitung kebarangkalian bahawa dua orang daripada mereka akan memakai baju kemeja berwarna biru.
Penyelesaian:
$$ \begin{aligned} & P(\text { Jacky biru })=\frac{3}{8}, P(\text { Jacky bukan biru })=\frac{5}{8} \\ & P(\text { Halim biru })=\frac{2}{5}, P(\text { Halim bukan biru })=\frac{3}{5} \\ & P(\text { Kumar biru })=\frac{1}{5}, P(\text { Kumar bukan biru })=\frac{4}{5} \end{aligned} $$
$$ \begin{aligned} &\text { Kebarangkalian dua orang memakai baju biru }\\ &\begin{aligned} & =P(J b, H b, K b b)+P(J b, H b b, K b)+P(J b b, H b, K b) \\ & =\left(\frac{3}{8} \times \frac{2}{5} \times \frac{4}{5}\right)+\left(\frac{3}{8} \times \frac{3}{5} \times \frac{1}{5}\right)+\left(\frac{5}{8} \times \frac{2}{5} \times \frac{1}{5}\right) \\ & =\frac{3}{25}+\frac{9}{200}+\frac{1}{20} \\ & =\frac{43}{200} \end{aligned} \end{aligned} $$
Soalan 10:
Carta bar di bawah menunjukkan bilangan kelab badminton dan kelab bina badan dalam negeri Kedah, Negeri Sembilan, Wilayah Persekutuan Labuan dan Wilayah Persekutuan Putrajaya.
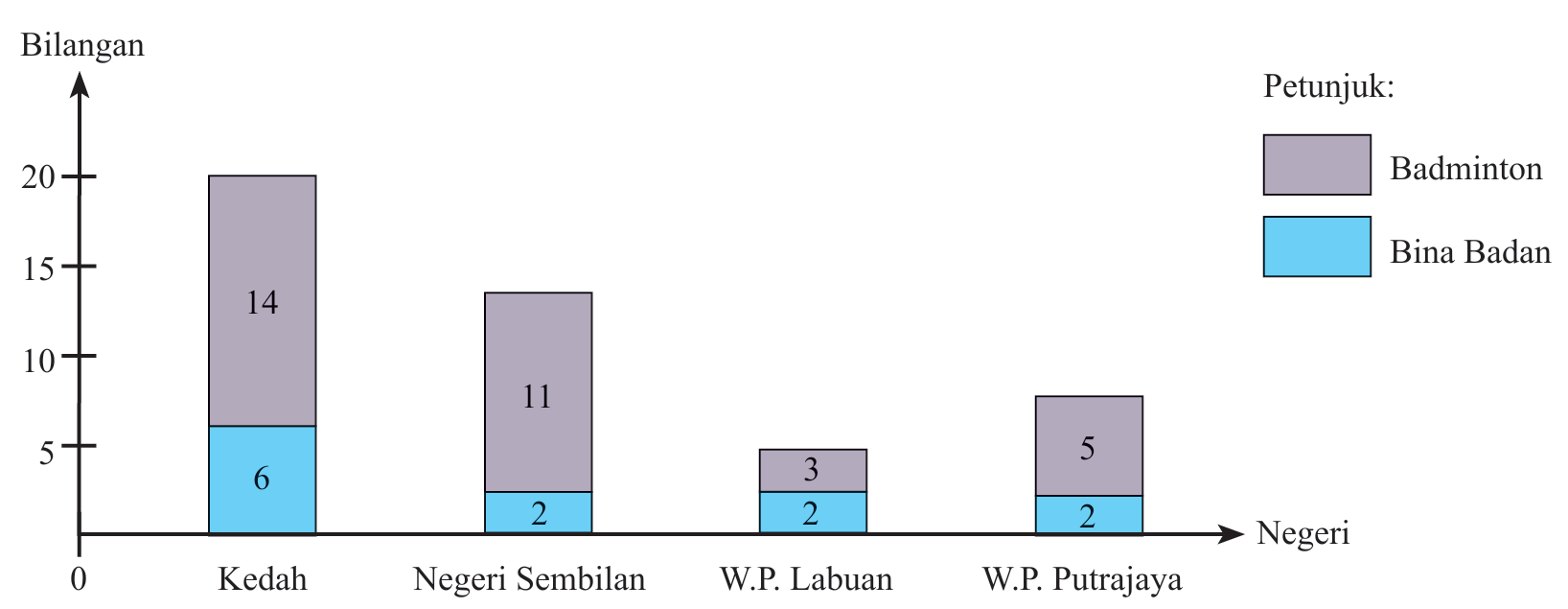
Sebuah kelab badminton dan sebuah kelab bina badan dipilih secara rawak dari empat negeri ini. Hitung kebarangkalian
(a) kedua-dua kelab yang dipilih adalah dari negeri Kedah.
(b) sebuah kelab dipilih dari Wilayah Persekutuan dan Negeri Sembilan masing-masing.
Penyelesaian:
Jumlah bilangan kelab badminton = 33
Jumlah bilangan kelab bina badan = 12
(a)
$$ \begin{aligned} & P(\text { kedua – dua kelab dari negeri Kedah }) \\ & =\frac{14}{33} \times \frac{6}{12} \\ & =\frac{7}{33} \end{aligned} $$
(b)
$$ \begin{aligned} & P(W \cdot P \text { badminton, Negeri Sembilan bina badan })+ \\ & P(W \cdot P \text { bina badan,Negeri Sembilan badminton }) \\ & =\left(\frac{8}{33} \times \frac{2}{12}\right)+\left(\frac{4}{12} \times \frac{11}{33}\right) \\ & =\frac{5}{33} \end{aligned} $$
Carta bar di bawah menunjukkan bilangan kelab badminton dan kelab bina badan dalam negeri Kedah, Negeri Sembilan, Wilayah Persekutuan Labuan dan Wilayah Persekutuan Putrajaya.

Sebuah kelab badminton dan sebuah kelab bina badan dipilih secara rawak dari empat negeri ini. Hitung kebarangkalian
(a) kedua-dua kelab yang dipilih adalah dari negeri Kedah.
(b) sebuah kelab dipilih dari Wilayah Persekutuan dan Negeri Sembilan masing-masing.
Penyelesaian:
Jumlah bilangan kelab badminton = 33
Jumlah bilangan kelab bina badan = 12
(a)
$$ \begin{aligned} & P(\text { kedua – dua kelab dari negeri Kedah }) \\ & =\frac{14}{33} \times \frac{6}{12} \\ & =\frac{7}{33} \end{aligned} $$
(b)
$$ \begin{aligned} & P(W \cdot P \text { badminton, Negeri Sembilan bina badan })+ \\ & P(W \cdot P \text { bina badan,Negeri Sembilan badminton }) \\ & =\left(\frac{8}{33} \times \frac{2}{12}\right)+\left(\frac{4}{12} \times \frac{11}{33}\right) \\ & =\frac{5}{33} \end{aligned} $$
Soalan 11:
Kebarangkalian Khaizan terbabit dalam kemalangan pada setiap pusingan perlumbaan motosikal ialah 0.4. Khaizan perlu meninggalkan perlumbaan motosikal sekiranya dia terlibat dalam kemalangan. Kebarangkalian Khaizan menang pada setiap pusingan perlumbaan motosikal ialah 0.96 dengan syarat dia tidak terlibat dalam kemalangan. Khaizan perlu berlumba tiga pusingan dalam suatu perlumbaan.
(a) Hitung kebarangkalian, betul kepada tiga tempat perpuluhan, bahawa
(i) Khaizan menjadi juara dalam perlumbaan tersebut,
(ii) Khaizan tidak dapat menghabiskan perlumbaan tersebut.
(b) Berdasarkan jawapan daripada (a), adakah wajar Khaizan menasihati adiknya untuk menyertai perlumbaan motosikal? Nyatakan satu nilai murni yang telah anda pelajari untuk menyokong jawapan tersebut.
Penyelesaian:
(a)(i)
$$ \begin{aligned} & \text { Kebarangkalian Khaizan menjadi juara } \\ & =P(\text { Tiada kemalangan serta menang dalam setiap pusingan })^3 \\ & =(0.6 \times 0.96)^3 \\ & =0.191 \text { (t.t.p }) \end{aligned} $$
(a)(ii)
$$ P(\text { kemalangan tidak berlaku })=1-0.4=0.6 $$
$$ \begin{aligned} & \text { Kebarangkalian Khaizan tidak dapat menghabiskan perlumbaan } \\ &= P(\text { kemalangan berlaku pada pusingan pertama) }+ \\ & P(\text { kemalangan berlaku pada pusingan kedua })+ \\ & P(\text { kemalangan berlaku pada pusingan ketiga }) \\ &= 0.4+(0.6)(0.4)+(0.6)(0.6)(0.4) \\ &= 0.184 \end{aligned} $$
(b)
Adalah tidak wajar Khaizan menasihati adiknya untuk menyertai perlumbaan motosikal.
Kita perlu sayangi nyawa.
Kebarangkalian Khaizan terbabit dalam kemalangan pada setiap pusingan perlumbaan motosikal ialah 0.4. Khaizan perlu meninggalkan perlumbaan motosikal sekiranya dia terlibat dalam kemalangan. Kebarangkalian Khaizan menang pada setiap pusingan perlumbaan motosikal ialah 0.96 dengan syarat dia tidak terlibat dalam kemalangan. Khaizan perlu berlumba tiga pusingan dalam suatu perlumbaan.
(a) Hitung kebarangkalian, betul kepada tiga tempat perpuluhan, bahawa
(i) Khaizan menjadi juara dalam perlumbaan tersebut,
(ii) Khaizan tidak dapat menghabiskan perlumbaan tersebut.
(b) Berdasarkan jawapan daripada (a), adakah wajar Khaizan menasihati adiknya untuk menyertai perlumbaan motosikal? Nyatakan satu nilai murni yang telah anda pelajari untuk menyokong jawapan tersebut.
Penyelesaian:
(a)(i)
$$ \begin{aligned} & \text { Kebarangkalian Khaizan menjadi juara } \\ & =P(\text { Tiada kemalangan serta menang dalam setiap pusingan })^3 \\ & =(0.6 \times 0.96)^3 \\ & =0.191 \text { (t.t.p }) \end{aligned} $$
(a)(ii)
$$ P(\text { kemalangan tidak berlaku })=1-0.4=0.6 $$
$$ \begin{aligned} & \text { Kebarangkalian Khaizan tidak dapat menghabiskan perlumbaan } \\ &= P(\text { kemalangan berlaku pada pusingan pertama) }+ \\ & P(\text { kemalangan berlaku pada pusingan kedua })+ \\ & P(\text { kemalangan berlaku pada pusingan ketiga }) \\ &= 0.4+(0.6)(0.4)+(0.6)(0.6)(0.4) \\ &= 0.184 \end{aligned} $$
(b)
Adalah tidak wajar Khaizan menasihati adiknya untuk menyertai perlumbaan motosikal.
Kita perlu sayangi nyawa.