Soalan 1:
Kajian tentang jantina anak terhadap 16 000 keluarga yang mempunyai dua orang anak telah dijalankan. Anggarkan bilangan keluarga yang mempunyai sekurang-kurangnya seorang anak lelaki dalam kajian tersebut.
Penyelesaian:
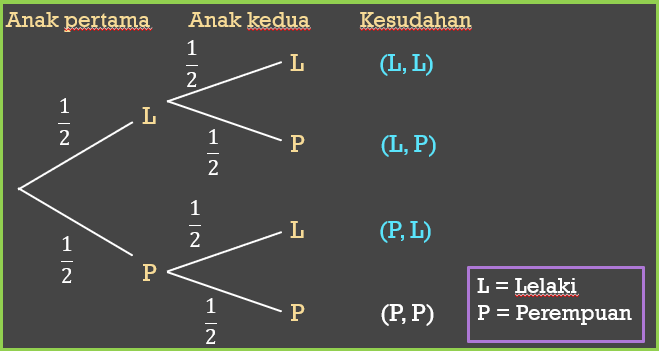
\begin{aligned} P(L, L)+P(L, P)+P(P, L) & =\left(\frac{1}{2} \times \frac{1}{2}\right)+\left(\frac{1}{2} \times \frac{1}{2}\right)+\left(\frac{1}{2} \times \frac{1}{2}\right) \\ & =\frac{3}{4} \end{aligned}
$$ \begin{aligned} &\text { Maka, bilangan keluarga sekurang-kurangnya mempunyai seorang anak lelaki }\\ &\begin{aligned} & =\frac{3}{4} \times 16000 \\ & =12000 \end{aligned} \end{aligned} $$
Kajian tentang jantina anak terhadap 16 000 keluarga yang mempunyai dua orang anak telah dijalankan. Anggarkan bilangan keluarga yang mempunyai sekurang-kurangnya seorang anak lelaki dalam kajian tersebut.
Penyelesaian:

\begin{aligned} P(L, L)+P(L, P)+P(P, L) & =\left(\frac{1}{2} \times \frac{1}{2}\right)+\left(\frac{1}{2} \times \frac{1}{2}\right)+\left(\frac{1}{2} \times \frac{1}{2}\right) \\ & =\frac{3}{4} \end{aligned}
$$ \begin{aligned} &\text { Maka, bilangan keluarga sekurang-kurangnya mempunyai seorang anak lelaki }\\ &\begin{aligned} & =\frac{3}{4} \times 16000 \\ & =12000 \end{aligned} \end{aligned} $$
Soalan 2:
Sebuah kotak mengandungi tiga batang pen kuning, lima batang pen merah dan sebatang pen hitam. Dua batang pen dipilih secara rawak dari kotak. Hitung kebarangkalian bahawa kedua-dua batang pen yang dipilih berwarna sama.
Penyelesaian:
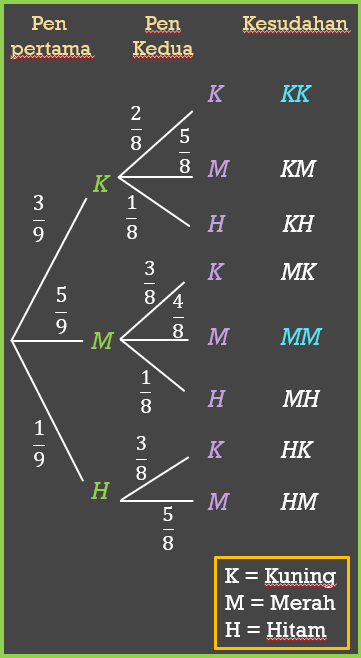
$$ \begin{aligned} & P \text { (Kedua-dua batang pen berwarna sama) } \\ & =P(K, K)+P(M, M) \\ & =\left(\frac{3}{9} \times \frac{2}{8}\right)+\left(\frac{5}{9} \times \frac{4}{8}\right) \\ & =\frac{13}{36} \end{aligned} $$
Sebuah kotak mengandungi tiga batang pen kuning, lima batang pen merah dan sebatang pen hitam. Dua batang pen dipilih secara rawak dari kotak. Hitung kebarangkalian bahawa kedua-dua batang pen yang dipilih berwarna sama.
Penyelesaian:

$$ \begin{aligned} & P \text { (Kedua-dua batang pen berwarna sama) } \\ & =P(K, K)+P(M, M) \\ & =\left(\frac{3}{9} \times \frac{2}{8}\right)+\left(\frac{5}{9} \times \frac{4}{8}\right) \\ & =\frac{13}{36} \end{aligned} $$
Soalan 3:
Jonathan suka menyaksikan matahari terbenam di tepi pantai. Jonathan mempunyai dua pilihan sama ada menginap di Pantai Jati atau Pantai Cengal selama dua hari. Kebarangkalian hujan di Pantai Jati pada setiap petang ialah 19/25.
Kebarangkalian hujan turun di Pantai Cengal pula bergantung pada hari sebelumnya. Jika hari sebelumnya tidak hujan, maka kebarangkalian hujan pada petang itu ialah 5/7. Jika hari sebelumnya hujan, maka kebarangkalian hujan pada petang itu ialah 2/5.
Jika cuaca cerah di kedua-dua pantai pada hari sebelum Jonathan bertolak, pantai yang manakah patut dipilih oleh Jonathan supaya dia dapat menyaksikan matahari terbenam di tepi pantai pada kedua-dua petang? Berikan justifikasi anda.
Penyelesaian:
$$ P(\text { Tidak hujan di Pantai Jati })=1-\frac{19}{25}=\frac{6}{25} $$
$$ \begin{aligned} & P(\text { Tidak hujan kedua -dua hari di Pantai Jati }) \\ & =\frac{6}{25} \times \frac{6}{25} \\ & =\frac{36}{625} \\ & =0.0576 \end{aligned} $$
$$ \begin{aligned} &\text { P(Tidak hujan di Pantai Cengal pada hari pertama) }\\ &=1-\frac{5}{7}=\frac{2}{7} \end{aligned} $$
$$ \begin{aligned} &\text { P(Tidak hujan kedua-dua hari di Pantai Cengal) }\\ &\begin{aligned} & =\frac{2}{7} \times \frac{2}{7} \\ & =\frac{4}{49} \\ & =0.0816 \end{aligned} \end{aligned} $$
Maka, Jonathan patut pergi Pantai Cengal kerana kebarangkalian tidak hujan bagi kedua-dua hari di Pantai Cengal lebih tinggi.
Jonathan suka menyaksikan matahari terbenam di tepi pantai. Jonathan mempunyai dua pilihan sama ada menginap di Pantai Jati atau Pantai Cengal selama dua hari. Kebarangkalian hujan di Pantai Jati pada setiap petang ialah 19/25.
Kebarangkalian hujan turun di Pantai Cengal pula bergantung pada hari sebelumnya. Jika hari sebelumnya tidak hujan, maka kebarangkalian hujan pada petang itu ialah 5/7. Jika hari sebelumnya hujan, maka kebarangkalian hujan pada petang itu ialah 2/5.
Jika cuaca cerah di kedua-dua pantai pada hari sebelum Jonathan bertolak, pantai yang manakah patut dipilih oleh Jonathan supaya dia dapat menyaksikan matahari terbenam di tepi pantai pada kedua-dua petang? Berikan justifikasi anda.
Penyelesaian:
$$ P(\text { Tidak hujan di Pantai Jati })=1-\frac{19}{25}=\frac{6}{25} $$
$$ \begin{aligned} & P(\text { Tidak hujan kedua -dua hari di Pantai Jati }) \\ & =\frac{6}{25} \times \frac{6}{25} \\ & =\frac{36}{625} \\ & =0.0576 \end{aligned} $$
$$ \begin{aligned} &\text { P(Tidak hujan di Pantai Cengal pada hari pertama) }\\ &=1-\frac{5}{7}=\frac{2}{7} \end{aligned} $$
$$ \begin{aligned} &\text { P(Tidak hujan kedua-dua hari di Pantai Cengal) }\\ &\begin{aligned} & =\frac{2}{7} \times \frac{2}{7} \\ & =\frac{4}{49} \\ & =0.0816 \end{aligned} \end{aligned} $$
Maka, Jonathan patut pergi Pantai Cengal kerana kebarangkalian tidak hujan bagi kedua-dua hari di Pantai Cengal lebih tinggi.
Soalan 4:
Setiap pelanggan Kedai Naga yang berbelanja melebihi RM200 akan diberi peluang memutar roda bertuah yang mempunyai enam sektor yang sama. Dua daripada sektor roda bertuah itu berwarna merah dan yang lain berwarna kuning.
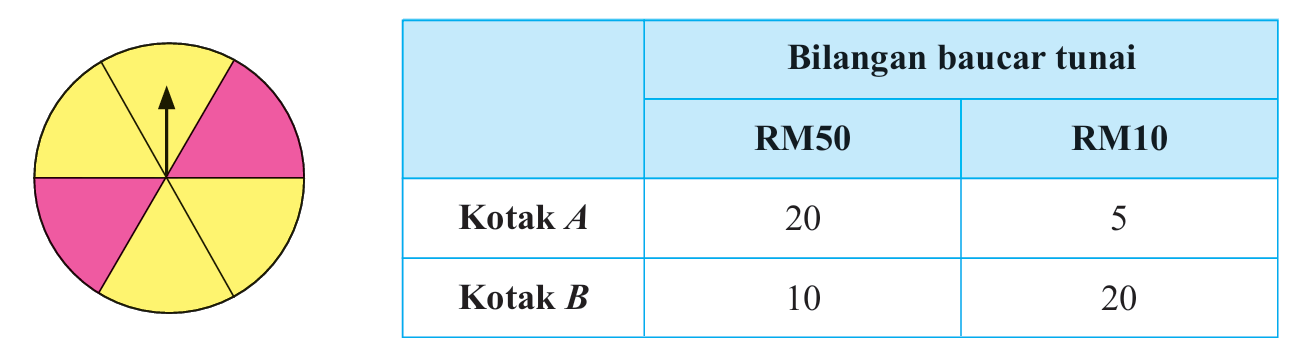
Jika jarum putaran roda bertuah berhenti di sektor berwarna merah, pelanggan tersebut berpeluang memilih baucar tunai dari kotak A. Jika jarum putaran roda bertuah berhenti di sektor berwarna kuning, pelanggan tersebut berpeluang memilih baucar tunai dari kotak B. Bilangan baucar tunai yang terdapat dalam kotak A dan kotak B ditunjukkan dalam jadual di atas.
Dianggarkan sebanyak 450 pelanggan Kedai Naga akan berbelanja melebihi RM200. Hitung bilangan baucar tunai bernilai RM10 yang perlu disediakan oleh Kedai Naga. (Baucar tunai yang telah dipilih akan digantikan dengan baucar yang baharu oleh Kedai Naga supaya bilangan baucar tunai dalam kedua-dua kotak A dan B sentiasa kekal).
Penyelesaian:
$$ \begin{aligned} &\begin{aligned} & P(\text { Sektor Merah })=\frac{2}{6} \\ & P(\text { Sektor Kuning })=\frac{4}{6} \end{aligned}\\ &P(\text { Kotak } A \text { dengan baucer } R M 10)=\frac{5}{25}\\ &P(\text { Kotak } B \text { dengan baucer } R M 10)=\frac{20}{30} \end{aligned} $$
$$ \begin{aligned} &P(\text { Merah, Kotak A baucer RM10) }+P(\text { Kuning, Kotak B baucer RM10) }\\ &\begin{aligned} & =\left(\frac{2}{6} \times \frac{5}{25}\right)+\left(\frac{4}{6} \times \frac{20}{30}\right) \\ & =\frac{23}{45} \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Maka, bilangan baucar tunai bernilai RM10 yang perlu disediakan }\\ &\begin{aligned} \text { oleh Kedai Naga } & =\frac{23}{45} \times 450 \\ & =230 \end{aligned} \end{aligned} $$
Setiap pelanggan Kedai Naga yang berbelanja melebihi RM200 akan diberi peluang memutar roda bertuah yang mempunyai enam sektor yang sama. Dua daripada sektor roda bertuah itu berwarna merah dan yang lain berwarna kuning.

Jika jarum putaran roda bertuah berhenti di sektor berwarna merah, pelanggan tersebut berpeluang memilih baucar tunai dari kotak A. Jika jarum putaran roda bertuah berhenti di sektor berwarna kuning, pelanggan tersebut berpeluang memilih baucar tunai dari kotak B. Bilangan baucar tunai yang terdapat dalam kotak A dan kotak B ditunjukkan dalam jadual di atas.
Dianggarkan sebanyak 450 pelanggan Kedai Naga akan berbelanja melebihi RM200. Hitung bilangan baucar tunai bernilai RM10 yang perlu disediakan oleh Kedai Naga. (Baucar tunai yang telah dipilih akan digantikan dengan baucar yang baharu oleh Kedai Naga supaya bilangan baucar tunai dalam kedua-dua kotak A dan B sentiasa kekal).
Penyelesaian:
$$ \begin{aligned} &\begin{aligned} & P(\text { Sektor Merah })=\frac{2}{6} \\ & P(\text { Sektor Kuning })=\frac{4}{6} \end{aligned}\\ &P(\text { Kotak } A \text { dengan baucer } R M 10)=\frac{5}{25}\\ &P(\text { Kotak } B \text { dengan baucer } R M 10)=\frac{20}{30} \end{aligned} $$
$$ \begin{aligned} &P(\text { Merah, Kotak A baucer RM10) }+P(\text { Kuning, Kotak B baucer RM10) }\\ &\begin{aligned} & =\left(\frac{2}{6} \times \frac{5}{25}\right)+\left(\frac{4}{6} \times \frac{20}{30}\right) \\ & =\frac{23}{45} \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Maka, bilangan baucar tunai bernilai RM10 yang perlu disediakan }\\ &\begin{aligned} \text { oleh Kedai Naga } & =\frac{23}{45} \times 450 \\ & =230 \end{aligned} \end{aligned} $$