5.7.1 SPM Praktis (Soalan Panjang)
Soalan 1:
Rajah di bawah menunjukkan sebuah trapezium, ABCD yang dilukis pada satah Cartesan. BC selari dengan AD dan O ialah asalan. Persamaan garis lurus BC ialah 3y = kx + 7 dan persamaan garis lurus AD ialah
y=12x+3.
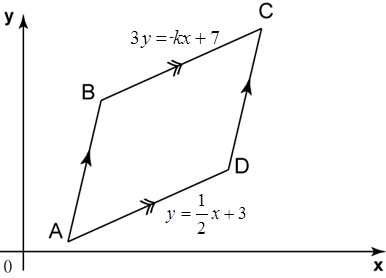
Cari
(a) nilai k,
(b) pintasan-x bagi garis lurus BC.
Penyelesaian:
(a)
Persamaan BC:
3y = kx + 7
y=k3x+73∴KecerunanBC=k3PersamaanAD:y=12x+3∴KecerunanAD=12
KecerunanBC=kecerunanADk3=12∴k=32
(b)
Persamaan,
3y=32x+7
Pada pintasan-x, y = 0
3(0)=32x+732x=−7x=−143
Oleh itu, pintasan-x bagi garis lurus BC = −143
Soalan 2:
Dalam rajah di bawah, O ialah asalan. Garis lurus MN adalah selari dengan garis lurus OK.
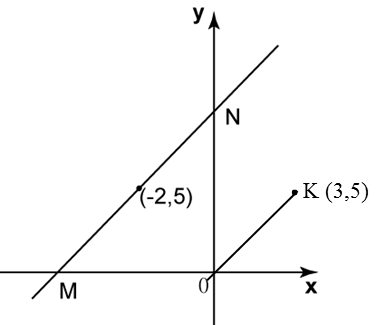
Cari
(a) persamaan bagi garis lurus MN,
(b) pintasan-x bagi garis lurus MN.
Penyelesaian:
(a) Kecerunan MN = kecerunan OK
=5−03−0=53
Gantikan = 5/3 dan (–2, 5) ke dalam y = mx+ c
5=53(−2)+c
15 = –10 + 3c
3c = 25
c = 25/3
Oleh itu, persamaan MN:
y=53x+253
(b)
Pada pintasan-x, y = 0
0=53x+25353x=−253
5x = –25
x = –5
Oleh itu, pintasan-x bagi MN = –5.
Soalan 3:
Rajah di bawah menunjukkan suatu garis lurus JK dan garis lurus ST dilukis pada satah Cartesan. JK adalah selari dengan ST.
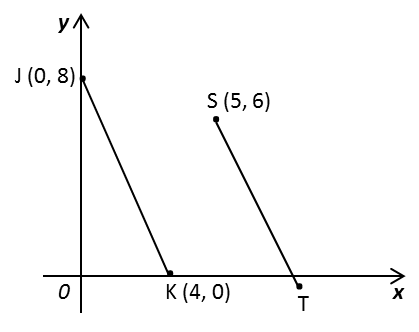
Cari
(a) persamaan bagi garis lurus ST,
(b) pintasan-x bagi garis lurus ST.
Penyelesaian:
(a)
JK adalah selari dengan ST, kecerunan JK = kecerunan ST.
=8−00−4=−2
Gantikan m = –2 dan S (5, 6) ke dalam y = mx+ c
6 = –2 (5) + c
c = 16
Oleh itu, persamaan ST : y = –2x + 16
(b)
Pada pintasan-x, y = 0
0 = –2x + 16
2x = 16
x = 8
Oleh itu, pintasan-x bagi ST = 8.