Soalan 1:
Masa, t dalam jam, diambil untuk memotong rumput di sebuah padang berubah secara langsung dengan luas, L dalam m2, dan secara songsang dengan bilangan pekerja, w. Diberi bahawa 5 orang pekerja mengambil masa selama 3 jam untuk memotong rumput seluas 4 × 104 m2.
(b)
$$ \begin{aligned} &\begin{aligned} & \text { Diberi } w=5, t=3, L=4 \times 10^4 \\ & \begin{aligned} 3 & =\frac{k\left(4 \times 10^4\right)}{5} \\ k & =\frac{15}{4 \times 10^4} \\ & =\frac{3}{8000} \end{aligned} \end{aligned}\\ &\text { Maka, } t=\frac{3 L}{8000 w} \end{aligned} $$
$$ \begin{aligned} & \text { Apabila } t=8, L=1.6 \times 10^5 \\ & 8=\frac{3\left(1.6 \times 10^5\right)}{8000 w} \\ & w=\frac{3\left(1.6 \times 10^5\right)}{8000 \times 8} \\ & =7.5 \\ & =8 \text { orang pekerja (minima) } \end{aligned} $$
Masa, t dalam jam, diambil untuk memotong rumput di sebuah padang berubah secara langsung dengan luas, L dalam m2, dan secara songsang dengan bilangan pekerja, w. Diberi bahawa 5 orang pekerja mengambil masa selama 3 jam untuk memotong rumput seluas 4 × 104 m2.
(a) Cari persamaan yang menghubungkaitkan t dalam sebutanL dan w. [2 markah]
(b) Hitung bilangan pekerja minima yang diperlukan untuk memotong rumput seluas 1.6 × 105 m2 dalam masa 8 jam. [2 markah]
Penyelesaian:
(a)
$$
\begin{aligned}
& t \propto L \\
& t \propto \frac{1}{w} \\
& t \propto \frac{L}{w} \\
& t=\frac{k L}{w}
\end{aligned}
$$
(b)
$$ \begin{aligned} &\begin{aligned} & \text { Diberi } w=5, t=3, L=4 \times 10^4 \\ & \begin{aligned} 3 & =\frac{k\left(4 \times 10^4\right)}{5} \\ k & =\frac{15}{4 \times 10^4} \\ & =\frac{3}{8000} \end{aligned} \end{aligned}\\ &\text { Maka, } t=\frac{3 L}{8000 w} \end{aligned} $$
$$ \begin{aligned} & \text { Apabila } t=8, L=1.6 \times 10^5 \\ & 8=\frac{3\left(1.6 \times 10^5\right)}{8000 w} \\ & w=\frac{3\left(1.6 \times 10^5\right)}{8000 \times 8} \\ & =7.5 \\ & =8 \text { orang pekerja (minima) } \end{aligned} $$
Soalan 2:
Rajah 1 di ruang jawapan menunjukkan segi empat sama PQRS yang dilukis pada grid segi empat sama bersisi 1 unit. Y adalah titik yang bergerak di dalam segi empat sama itu.
(a) Pada Rajah 1, lukis lokus bagi titik Y yang sentiasa bergerak 3 unit dari titik K. [1 markah]
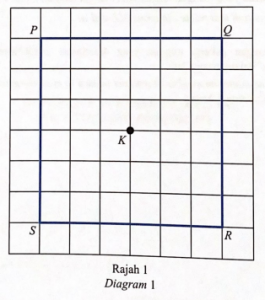
(b) Hitung jarak yang dilalui oleh lokus Y yang dilukis pada 2(a). [2 markah]
Penyelesaian:
(a)
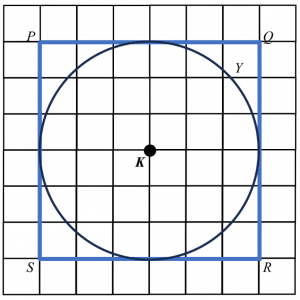
(b)
$$ \begin{aligned} &\text { Jarak yang dilalui oleh lokus } Y \text { (lilitan bulatan) }\\ &\begin{aligned} & =2 \times \pi \times j \\ & =2 \times \frac{22}{7} \times 3 \\ & =\frac{132}{7}=18 \frac{6}{7} \mathrm{unit} \end{aligned} \end{aligned} $$
Rajah 1 di ruang jawapan menunjukkan segi empat sama PQRS yang dilukis pada grid segi empat sama bersisi 1 unit. Y adalah titik yang bergerak di dalam segi empat sama itu.
(a) Pada Rajah 1, lukis lokus bagi titik Y yang sentiasa bergerak 3 unit dari titik K. [1 markah]

(b) Hitung jarak yang dilalui oleh lokus Y yang dilukis pada 2(a). [2 markah]
Penyelesaian:
(a)

(b)
$$ \begin{aligned} &\text { Jarak yang dilalui oleh lokus } Y \text { (lilitan bulatan) }\\ &\begin{aligned} & =2 \times \pi \times j \\ & =2 \times \frac{22}{7} \times 3 \\ & =\frac{132}{7}=18 \frac{6}{7} \mathrm{unit} \end{aligned} \end{aligned} $$