Soalan 11:
Hasil tambah bagi suatu set 10 nombor ialah 180 dan hasil tambah kuasa dua bagi set nombor ini ialah 3 800.
(a) Hitung min dan varians bagi nombor-nombor ini.
(b) Nombor 19 ditambah kepada set nombor-nombor ini. Hitung min dan varians yang baharu.
Penyelesaian:
(a)
$$ \text { Diberi } \sum x=180, \quad \sum x^2=3800 $$
$$ \begin{aligned} \operatorname{Min} & =\frac{\sum x}{N} \\ & =\frac{180}{10} \\ & =18 \end{aligned} $$
$$ \begin{aligned} \text { Varians } & =\frac{\sum x^2}{N}-(\bar{x})^2 \\ & =\frac{3800}{10}-(18)^2 \\ & =380-324 \\ & =56 \end{aligned} $$
(b)
$$ \begin{aligned} & \sum x \text { baharu }=180+19=199 \\ & \sum x^2 \text { baharu }=3800+19^2=4161 \end{aligned} $$
$$ \begin{aligned} \text { Min baharu } & =\frac{199}{11} \\ & =18.09 \end{aligned} $$
$$ \begin{aligned} \text { Varians baharu } & =\frac{4161}{11}-(18.09)^2 \\ & =51.02 \end{aligned} $$
Hasil tambah bagi suatu set 10 nombor ialah 180 dan hasil tambah kuasa dua bagi set nombor ini ialah 3 800.
(a) Hitung min dan varians bagi nombor-nombor ini.
(b) Nombor 19 ditambah kepada set nombor-nombor ini. Hitung min dan varians yang baharu.
Penyelesaian:
(a)
$$ \text { Diberi } \sum x=180, \quad \sum x^2=3800 $$
$$ \begin{aligned} \operatorname{Min} & =\frac{\sum x}{N} \\ & =\frac{180}{10} \\ & =18 \end{aligned} $$
$$ \begin{aligned} \text { Varians } & =\frac{\sum x^2}{N}-(\bar{x})^2 \\ & =\frac{3800}{10}-(18)^2 \\ & =380-324 \\ & =56 \end{aligned} $$
(b)
$$ \begin{aligned} & \sum x \text { baharu }=180+19=199 \\ & \sum x^2 \text { baharu }=3800+19^2=4161 \end{aligned} $$
$$ \begin{aligned} \text { Min baharu } & =\frac{199}{11} \\ & =18.09 \end{aligned} $$
$$ \begin{aligned} \text { Varians baharu } & =\frac{4161}{11}-(18.09)^2 \\ & =51.02 \end{aligned} $$
Soalan 12:
Jadual di bawah menunjukkan masa yang diluangkan, dalam jam, untuk mengulang kaji dalam seminggu oleh 32 orang murid.

(a) Hitung julat , julat antara kuartil, varians dan sisihan piawai bagi taburan ini.
(b) Nyatakan sukatan serakan yang lebih sesuai digunakan untuk memberikan suatu gambaran yang lebih jelas berkenaan masa ulang kaji bagi kumpulan murid ini.
Penyelesaian:
(a)
Julat = 10 – 1 = 9
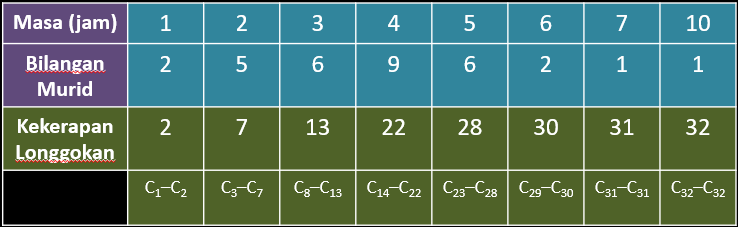
$$ \begin{aligned} & Q_1=\frac{1}{4} \times 32=\text { cerapan } k e-8 \\ & Q_3=\frac{3}{4} \times 32=\text { cerapan } k e-24 \end{aligned} $$
$$ \begin{aligned} \text { Julat antara kuartil } & =Q_3-Q_1 \\ & =5-3 \\ & =2 \end{aligned} $$
$$ \begin{aligned} &\text { Varians, } \sigma^2\\ &\begin{aligned} = & \frac{2(1)^2+5(2)^2+6(3)^2+9(4)^2+6(5)^2+2(6)^2+1(7)^2+1(10)^2}{32} \\ & \quad-\left(\frac{2(1)+5(2)+6(3)+9(4)+6(5)+2(6)+1(7)+1(10)}{32}\right)^2 \\ = & 18.469-15.259 \\ = & 3.210 \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Sisihan piawai } & =\sqrt{\text { varians }} \\ & =\sqrt{3.210} \\ & =1.792 \end{aligned} $$
(b) Sukatan serakan yang lebih sesuai digunakan adalah julat antara kuartil.
Jadual di bawah menunjukkan masa yang diluangkan, dalam jam, untuk mengulang kaji dalam seminggu oleh 32 orang murid.

(a) Hitung julat , julat antara kuartil, varians dan sisihan piawai bagi taburan ini.
(b) Nyatakan sukatan serakan yang lebih sesuai digunakan untuk memberikan suatu gambaran yang lebih jelas berkenaan masa ulang kaji bagi kumpulan murid ini.
Penyelesaian:
(a)
Julat = 10 – 1 = 9
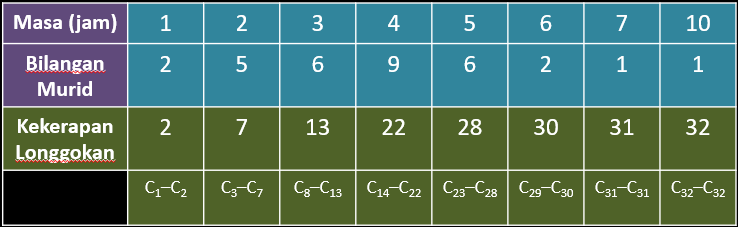
$$ \begin{aligned} & Q_1=\frac{1}{4} \times 32=\text { cerapan } k e-8 \\ & Q_3=\frac{3}{4} \times 32=\text { cerapan } k e-24 \end{aligned} $$
$$ \begin{aligned} \text { Julat antara kuartil } & =Q_3-Q_1 \\ & =5-3 \\ & =2 \end{aligned} $$
$$ \begin{aligned} &\text { Varians, } \sigma^2\\ &\begin{aligned} = & \frac{2(1)^2+5(2)^2+6(3)^2+9(4)^2+6(5)^2+2(6)^2+1(7)^2+1(10)^2}{32} \\ & \quad-\left(\frac{2(1)+5(2)+6(3)+9(4)+6(5)+2(6)+1(7)+1(10)}{32}\right)^2 \\ = & 18.469-15.259 \\ = & 3.210 \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Sisihan piawai } & =\sqrt{\text { varians }} \\ & =\sqrt{3.210} \\ & =1.792 \end{aligned} $$
(b) Sukatan serakan yang lebih sesuai digunakan adalah julat antara kuartil.