Soalan 4:
Diberi y = 0.5 apabila x = 16, hitung nilai y apabila x = 0.04 jika

Penyelesaian:
(a)
$$ \begin{aligned} &\begin{aligned} & y \alpha \frac{1}{x} \\ & y=\frac{k}{x} \end{aligned}\\ &\text { Diberi } x=16, y=0.5 \end{aligned} $$
$$ \begin{aligned} 0.5 & =\frac{k}{16} \\ k & =0.5 \times 16 \\ k & =8 \\ \text { Maka, } y & =\frac{8}{x} \end{aligned} $$
$$ \begin{aligned} \text { Apabila } x & =0.04 \\ y & =\frac{8}{0.04} \\ y & =200 \end{aligned} $$
(b)
$$ \begin{aligned} &\begin{aligned} & y \alpha \frac{1}{x^3} \\ & y=\frac{k}{x^3} \end{aligned}\\ &\text { Diberi } x=16, y=0.5 \end{aligned} $$
$$ \begin{aligned} &\begin{aligned} 0.5 & =\frac{k}{16^3} \\ k & =0.5 \times 16^3 \\ k & =2048 \end{aligned}\\ &\text { Maka, } y=\frac{2048}{x^3} \end{aligned} $$
$$ \begin{aligned} & \text { Apabila } x=0.04 \\ & \qquad \begin{aligned} y & =\frac{2048}{0.04^3} \\ y & =32000000 \end{aligned} \end{aligned} $$
(c)
$$ \begin{gathered} y \alpha \frac{1}{x^{\frac{1}{2}}} \\ y=\frac{k}{x^{\frac{1}{2}}} \\ \text { Diberi } x=16, y=0.5 \end{gathered} $$
$$ \begin{aligned} 0.5 & =\frac{k}{16^{\frac{1}{2}}} \\ k & =0.5 \times 16^{\frac{1}{2}} \\ k & =2 \\ \text { Maka, } y & =\frac{2}{x^{\frac{1}{2}}} \end{aligned} $$
$$ \begin{aligned} & \text { Apabila } x=0.04 \\ & \qquad \begin{aligned} y & =\frac{2}{(0.04)^{\frac{1}{2}}} \\ y & =10 \end{aligned} \end{aligned} $$
(d)
$$ \begin{aligned} &\begin{aligned} & y \alpha \frac{1}{\sqrt[3]{x}} \\ & y=\frac{k}{\sqrt[3]{x}} \end{aligned}\\ &\text { Diberi } x=16, y=0.5 \end{aligned} $$
$$ \begin{aligned} 0.5 & =\frac{k}{\sqrt[3]{16}} \\ k & =0.5 \times \sqrt[3]{16} \\ k & =1.26 \\ \text { Maka, } y & =\frac{1.26}{\sqrt[3]{x}} \end{aligned} $$
$$ \begin{gathered} \text { Apabila } x=0.04 \\ \begin{array}{c} y=\frac{1.26}{\sqrt[3]{0.04}} \\ y=3.684 \end{array} \end{gathered} $$
Diberi y = 0.5 apabila x = 16, hitung nilai y apabila x = 0.04 jika

Penyelesaian:
(a)
$$ \begin{aligned} &\begin{aligned} & y \alpha \frac{1}{x} \\ & y=\frac{k}{x} \end{aligned}\\ &\text { Diberi } x=16, y=0.5 \end{aligned} $$
$$ \begin{aligned} 0.5 & =\frac{k}{16} \\ k & =0.5 \times 16 \\ k & =8 \\ \text { Maka, } y & =\frac{8}{x} \end{aligned} $$
$$ \begin{aligned} \text { Apabila } x & =0.04 \\ y & =\frac{8}{0.04} \\ y & =200 \end{aligned} $$
(b)
$$ \begin{aligned} &\begin{aligned} & y \alpha \frac{1}{x^3} \\ & y=\frac{k}{x^3} \end{aligned}\\ &\text { Diberi } x=16, y=0.5 \end{aligned} $$
$$ \begin{aligned} &\begin{aligned} 0.5 & =\frac{k}{16^3} \\ k & =0.5 \times 16^3 \\ k & =2048 \end{aligned}\\ &\text { Maka, } y=\frac{2048}{x^3} \end{aligned} $$
$$ \begin{aligned} & \text { Apabila } x=0.04 \\ & \qquad \begin{aligned} y & =\frac{2048}{0.04^3} \\ y & =32000000 \end{aligned} \end{aligned} $$
(c)
$$ \begin{gathered} y \alpha \frac{1}{x^{\frac{1}{2}}} \\ y=\frac{k}{x^{\frac{1}{2}}} \\ \text { Diberi } x=16, y=0.5 \end{gathered} $$
$$ \begin{aligned} 0.5 & =\frac{k}{16^{\frac{1}{2}}} \\ k & =0.5 \times 16^{\frac{1}{2}} \\ k & =2 \\ \text { Maka, } y & =\frac{2}{x^{\frac{1}{2}}} \end{aligned} $$
$$ \begin{aligned} & \text { Apabila } x=0.04 \\ & \qquad \begin{aligned} y & =\frac{2}{(0.04)^{\frac{1}{2}}} \\ y & =10 \end{aligned} \end{aligned} $$
(d)
$$ \begin{aligned} &\begin{aligned} & y \alpha \frac{1}{\sqrt[3]{x}} \\ & y=\frac{k}{\sqrt[3]{x}} \end{aligned}\\ &\text { Diberi } x=16, y=0.5 \end{aligned} $$
$$ \begin{aligned} 0.5 & =\frac{k}{\sqrt[3]{16}} \\ k & =0.5 \times \sqrt[3]{16} \\ k & =1.26 \\ \text { Maka, } y & =\frac{1.26}{\sqrt[3]{x}} \end{aligned} $$
$$ \begin{gathered} \text { Apabila } x=0.04 \\ \begin{array}{c} y=\frac{1.26}{\sqrt[3]{0.04}} \\ y=3.684 \end{array} \end{gathered} $$
Soalan 5:
Hitung nilai s dan nilai t bagi setiap hubungan berikut.
(a) y berubah secara songsang dengan x.
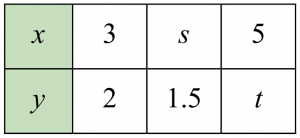
(b) y berubah secara songsang dengan punca kuasa dua x.
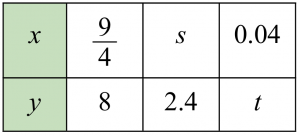
Penyelesaian:
(a)
$$ \begin{gathered} y \alpha \frac{1}{x} \\ y=\frac{k}{x} \\ \text { Diberi } x=3, y=2 \end{gathered} $$
$$ \begin{aligned} &\begin{aligned} 2 & =\frac{k}{3} \\ k & =2 \times 3 \\ k & =6 \end{aligned}\\ &\text { Maka, } y=\frac{6}{x} \end{aligned} $$
$$ \begin{aligned} &\text { Apabila } x=s, y=1.5\\ &\begin{aligned} 1.5 & =\frac{6}{s} \\ s & =\frac{6}{1.5} \\ s & =4 \end{aligned} \end{aligned} $$
$$ \begin{gathered} \text { Apabila } x=5, y=t \\ t=\frac{6}{5} \\ t=1.2 \end{gathered} $$
(b)
$$ \begin{aligned} & y \alpha \frac{1}{\sqrt{x}} \\ & y=\frac{k}{\sqrt{x}} \end{aligned} $$
$$ \begin{aligned} \text { Diberi } x & =\frac{9}{4}, y=8 \\ 8 & =\frac{k}{\sqrt{\frac{9}{4}}} \\ k & =8 \times \sqrt{\frac{9}{4}} \\ k & =12 \\ \text { Maka, } y & =\frac{12}{\sqrt{x}} \end{aligned} $$
$$ \begin{aligned} & \text { Apabila } x=s, y=2.4 \\ & 2.4=\frac{12}{\sqrt{s}} \\ & \sqrt{s}=\frac{12}{2.4} \\ & \sqrt{s}=5 \\ & s=5^2 \\ & s=25 \end{aligned} $$
$$ \begin{aligned} &\text { Apabila } x=0.04, y=t\\ &\begin{aligned} & t=\frac{12}{\sqrt{0.04}} \\ & t=60 \end{aligned} \end{aligned} $$
Hitung nilai s dan nilai t bagi setiap hubungan berikut.
(a) y berubah secara songsang dengan x.

(b) y berubah secara songsang dengan punca kuasa dua x.

Penyelesaian:
(a)
$$ \begin{gathered} y \alpha \frac{1}{x} \\ y=\frac{k}{x} \\ \text { Diberi } x=3, y=2 \end{gathered} $$
$$ \begin{aligned} &\begin{aligned} 2 & =\frac{k}{3} \\ k & =2 \times 3 \\ k & =6 \end{aligned}\\ &\text { Maka, } y=\frac{6}{x} \end{aligned} $$
$$ \begin{aligned} &\text { Apabila } x=s, y=1.5\\ &\begin{aligned} 1.5 & =\frac{6}{s} \\ s & =\frac{6}{1.5} \\ s & =4 \end{aligned} \end{aligned} $$
$$ \begin{gathered} \text { Apabila } x=5, y=t \\ t=\frac{6}{5} \\ t=1.2 \end{gathered} $$
(b)
$$ \begin{aligned} & y \alpha \frac{1}{\sqrt{x}} \\ & y=\frac{k}{\sqrt{x}} \end{aligned} $$
$$ \begin{aligned} \text { Diberi } x & =\frac{9}{4}, y=8 \\ 8 & =\frac{k}{\sqrt{\frac{9}{4}}} \\ k & =8 \times \sqrt{\frac{9}{4}} \\ k & =12 \\ \text { Maka, } y & =\frac{12}{\sqrt{x}} \end{aligned} $$
$$ \begin{aligned} & \text { Apabila } x=s, y=2.4 \\ & 2.4=\frac{12}{\sqrt{s}} \\ & \sqrt{s}=\frac{12}{2.4} \\ & \sqrt{s}=5 \\ & s=5^2 \\ & s=25 \end{aligned} $$
$$ \begin{aligned} &\text { Apabila } x=0.04, y=t\\ &\begin{aligned} & t=\frac{12}{\sqrt{0.04}} \\ & t=60 \end{aligned} \end{aligned} $$
Soalan 6:
Sebuah syarikat mencetak sejumlah buku setiap hari. Jadual di bawah menunjukkan bilangan buah mesin, M yang beroperasi dan masa yang diperlukan, T untuk mencetak buku-buku tersebut. Diberi T berubah secara songsang dengan M.
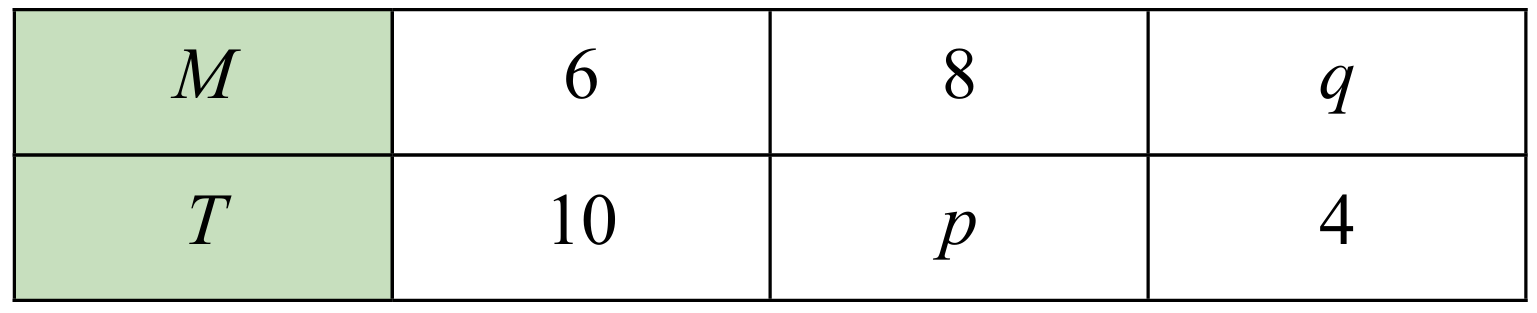
(a) Ungkapkan T dalam sebutan M.
(b) Tentukan nilai p dan nilai q.
Penyelesaian:
(a)
$$ \begin{aligned} &\begin{aligned} & T \alpha \frac{1}{M} \\ & T=\frac{k}{M} \end{aligned}\\ &\begin{aligned} \text { Diberi } T & =10, M=6 \\ 10 & =\frac{k}{6} \\ k & =10 \times 6 \\ k & =60 \\ \text { Maka, } T & =\frac{60}{M} \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Apabila } T=p, M=8\\ &\begin{aligned} p & =\frac{60}{8} \\ p & =7.5 \end{aligned}\\ &\begin{aligned} & \text { Apabila } T=4, M=q \\ & \qquad \begin{aligned} 4 & =\frac{60}{q} \\ q & =\frac{60}{4} \\ q & =15 \end{aligned} \end{aligned} \end{aligned} $$
Sebuah syarikat mencetak sejumlah buku setiap hari. Jadual di bawah menunjukkan bilangan buah mesin, M yang beroperasi dan masa yang diperlukan, T untuk mencetak buku-buku tersebut. Diberi T berubah secara songsang dengan M.

(a) Ungkapkan T dalam sebutan M.
(b) Tentukan nilai p dan nilai q.
Penyelesaian:
(a)
$$ \begin{aligned} &\begin{aligned} & T \alpha \frac{1}{M} \\ & T=\frac{k}{M} \end{aligned}\\ &\begin{aligned} \text { Diberi } T & =10, M=6 \\ 10 & =\frac{k}{6} \\ k & =10 \times 6 \\ k & =60 \\ \text { Maka, } T & =\frac{60}{M} \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Apabila } T=p, M=8\\ &\begin{aligned} p & =\frac{60}{8} \\ p & =7.5 \end{aligned}\\ &\begin{aligned} & \text { Apabila } T=4, M=q \\ & \qquad \begin{aligned} 4 & =\frac{60}{q} \\ q & =\frac{60}{4} \\ q & =15 \end{aligned} \end{aligned} \end{aligned} $$
Soalan 7:
Tempoh ayunan, T, bagi suatu bandul ringkas berubah secara songsang dengan punca kuasa dua pecutan graviti, g. Dalam satu ekpserimen, tempoh ayunan ialah 1.01 saat apabila pecutan graviti sebanyak 9.85 m s–2. Ungkapkan T dalam sebutan g.
Penyelesaian:
$$ \begin{aligned} &\begin{aligned} & T \propto \frac{1}{\sqrt{g}} \\ & T=\frac{k}{\sqrt{g}} \end{aligned}\\ &\text { Diberi } T=1.01, g=9.85 \end{aligned} $$
$$ \begin{aligned} 1.01 & =\frac{k}{\sqrt{9.85}} \\ k & =1.01(\sqrt{9.85}) \\ k & =3.17 \\ \text { Maka, } T & =\frac{3.17}{\sqrt{g}} \end{aligned} $$
Tempoh ayunan, T, bagi suatu bandul ringkas berubah secara songsang dengan punca kuasa dua pecutan graviti, g. Dalam satu ekpserimen, tempoh ayunan ialah 1.01 saat apabila pecutan graviti sebanyak 9.85 m s–2. Ungkapkan T dalam sebutan g.
Penyelesaian:
$$ \begin{aligned} &\begin{aligned} & T \propto \frac{1}{\sqrt{g}} \\ & T=\frac{k}{\sqrt{g}} \end{aligned}\\ &\text { Diberi } T=1.01, g=9.85 \end{aligned} $$
$$ \begin{aligned} 1.01 & =\frac{k}{\sqrt{9.85}} \\ k & =1.01(\sqrt{9.85}) \\ k & =3.17 \\ \text { Maka, } T & =\frac{3.17}{\sqrt{g}} \end{aligned} $$