Soalan 1:
Jadual di sebelah menunjukkan rintangan bagi seutas dawai yang berubah dengan keratan rentas jejari.
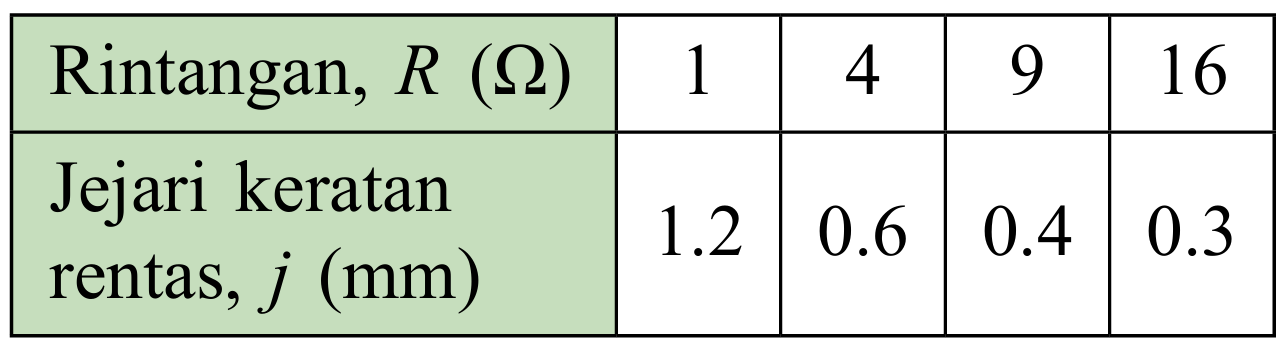
(a) Tentukan sama ada rintangan, R, bagi dawai ini berubah secara songsang dengan j2.
(b) Hitung jejari dawai dalam mm, jika rintangannya ialah 25 Ω.
Penyelesaian:
(a)
R berubah secara songsang dengan j2.
(b)
$$ \begin{aligned} & R \propto \frac{1}{j^2} \\ & R=\frac{k}{j^2} \\ & \text { Diberi } R=1, j=1.2 \\ & 1=\frac{k}{1.2^2} \end{aligned} $$
$$ \begin{aligned} & k=1 \times 1.2^2 \\ & k=1.44 \\ & \text { Maka, } R=\frac{1.44}{j^2} \\ & \text { Apabila } R=25 \\ & 25=\frac{1.44}{j^2} \end{aligned} $$
$$ \begin{aligned} j^2 & =\frac{1.44}{25} \\ j^2 & =0.0576 \\ j & =\sqrt{0.0576} \\ j & =0.24 \mathrm{~mm} \end{aligned} $$
Jadual di sebelah menunjukkan rintangan bagi seutas dawai yang berubah dengan keratan rentas jejari.
(a) Tentukan sama ada rintangan, R, bagi dawai ini berubah secara songsang dengan j2.
(b) Hitung jejari dawai dalam mm, jika rintangannya ialah 25 Ω.
Penyelesaian:
(a)
R berubah secara songsang dengan j2.(b)
$$ \begin{aligned} & R \propto \frac{1}{j^2} \\ & R=\frac{k}{j^2} \\ & \text { Diberi } R=1, j=1.2 \\ & 1=\frac{k}{1.2^2} \end{aligned} $$
$$ \begin{aligned} & k=1 \times 1.2^2 \\ & k=1.44 \\ & \text { Maka, } R=\frac{1.44}{j^2} \\ & \text { Apabila } R=25 \\ & 25=\frac{1.44}{j^2} \end{aligned} $$
$$ \begin{aligned} j^2 & =\frac{1.44}{25} \\ j^2 & =0.0576 \\ j & =\sqrt{0.0576} \\ j & =0.24 \mathrm{~mm} \end{aligned} $$
Soalan 2:
Bilangan kubus, b, yang dihasilkan daripada sejumlah kuantiti logam yang tetap berubah secara songsang dengan kuasa tiga sisinya, p cm. Jika b = 16 apabila p = 1.5, hitung nilai p apabila b = 250.
Penyelesaian:
$$ \begin{aligned} & b \alpha \frac{1}{p^3} \\ & b=\frac{k}{p^3} \end{aligned} $$
$$ \begin{aligned} & \text { Diberi } b=16, p=1.5 \\ & \qquad \begin{aligned} 16 & =\frac{k}{1.5^3} \\ k & =16\left(1.5^3\right) \\ k & =54 \\ \text { Maka, } b & =\frac{54}{p^3} \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Apabila } b & =250 \\ 250 & =\frac{54}{p^3} \\ p^3 & =\frac{54}{250} \\ p^3 & =0.216 \\ p & =\sqrt[3]{0.216} \\ p & =0.6 \mathrm{~cm} \end{aligned} $$
Bilangan kubus, b, yang dihasilkan daripada sejumlah kuantiti logam yang tetap berubah secara songsang dengan kuasa tiga sisinya, p cm. Jika b = 16 apabila p = 1.5, hitung nilai p apabila b = 250.
Penyelesaian:
$$ \begin{aligned} & b \alpha \frac{1}{p^3} \\ & b=\frac{k}{p^3} \end{aligned} $$
$$ \begin{aligned} & \text { Diberi } b=16, p=1.5 \\ & \qquad \begin{aligned} 16 & =\frac{k}{1.5^3} \\ k & =16\left(1.5^3\right) \\ k & =54 \\ \text { Maka, } b & =\frac{54}{p^3} \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Apabila } b & =250 \\ 250 & =\frac{54}{p^3} \\ p^3 & =\frac{54}{250} \\ p^3 & =0.216 \\ p & =\sqrt[3]{0.216} \\ p & =0.6 \mathrm{~cm} \end{aligned} $$
Soalan 3:
Bilangan ayunan, A bagi satu bandul ringkas berubah secara songsang dengan punca kuasa dua panjang bandul, p cm dalam suatu tempoh yang tetap. Diberi bahawa bilangan ayunan ialah 9 apabila panjang bandul ialah 36 cm, hitung panjang bandul ringkas jika bilangan ayunan ialah 15.
Penyelesaian:
$$ \begin{aligned} &\begin{aligned} & A \propto \frac{1}{\sqrt{p}} \\ & A=\frac{k}{\sqrt{p}} \end{aligned}\\ &\text { Diberi } A=9, p=36 \end{aligned} $$
$$ \begin{gathered} 9=\frac{k}{\sqrt{36}} \\ k=9(\sqrt{36}) \\ k=54 \\ \text { Maka, } A=\frac{54}{\sqrt{p}} \end{gathered} $$
$$ \begin{aligned} &\text { Apabila } A=15\\ &\begin{aligned} 15 & =\frac{54}{\sqrt{p}} \\ \sqrt{p} & =\frac{54}{15} \\ \sqrt{p} & =3.6 \\ p & =3.6^2 \\ p & =12.96 \mathrm{~cm} \end{aligned} \end{aligned} $$
Bilangan ayunan, A bagi satu bandul ringkas berubah secara songsang dengan punca kuasa dua panjang bandul, p cm dalam suatu tempoh yang tetap. Diberi bahawa bilangan ayunan ialah 9 apabila panjang bandul ialah 36 cm, hitung panjang bandul ringkas jika bilangan ayunan ialah 15.
Penyelesaian:
$$ \begin{aligned} &\begin{aligned} & A \propto \frac{1}{\sqrt{p}} \\ & A=\frac{k}{\sqrt{p}} \end{aligned}\\ &\text { Diberi } A=9, p=36 \end{aligned} $$
$$ \begin{gathered} 9=\frac{k}{\sqrt{36}} \\ k=9(\sqrt{36}) \\ k=54 \\ \text { Maka, } A=\frac{54}{\sqrt{p}} \end{gathered} $$
$$ \begin{aligned} &\text { Apabila } A=15\\ &\begin{aligned} 15 & =\frac{54}{\sqrt{p}} \\ \sqrt{p} & =\frac{54}{15} \\ \sqrt{p} & =3.6 \\ p & =3.6^2 \\ p & =12.96 \mathrm{~cm} \end{aligned} \end{aligned} $$