Soalan 5:
Diberi G berubah secara langsung dengan H dan punca kuasa dua M. Jika G = 42 apabila H = 7 dan M = 16, hitung
(a) nilai G apabila H = 4 dan M = 81,
(b) nilai M apabila G = 18 dan H = 20.
Penyelesaian:
$$ \text { Diberi } G=42, H=7, M=16 $$
$$ \begin{aligned} G & \alpha H \sqrt{M} \\ G & =k H \sqrt{M} \\ 42 & =k(7)(\sqrt{16}) \\ k & =\frac{42}{(7)(\sqrt{16})} \\ k & =\frac{3}{2} \\ \text { Maka } G & =\frac{3}{2} H \sqrt{M} \end{aligned} $$
(a)
$$ \begin{aligned} & \text { Apabila } H=4, M=81 \\ & \begin{aligned} G & =1.5(4)(\sqrt{81}) \\ & =54 \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Apabila } G=18, H=20\\ &\begin{aligned} 18 & =1.5(20)(\sqrt{M}) \\ \sqrt{M} & =\frac{18}{(1.5)(20)} \\ \sqrt{M} & =0.6 \\ M & =0.6^2 \\ M & =0.36 \end{aligned} \end{aligned} $$
Diberi G berubah secara langsung dengan H dan punca kuasa dua M. Jika G = 42 apabila H = 7 dan M = 16, hitung
(a) nilai G apabila H = 4 dan M = 81,
(b) nilai M apabila G = 18 dan H = 20.
Penyelesaian:
$$ \text { Diberi } G=42, H=7, M=16 $$
$$ \begin{aligned} G & \alpha H \sqrt{M} \\ G & =k H \sqrt{M} \\ 42 & =k(7)(\sqrt{16}) \\ k & =\frac{42}{(7)(\sqrt{16})} \\ k & =\frac{3}{2} \\ \text { Maka } G & =\frac{3}{2} H \sqrt{M} \end{aligned} $$
(a)
$$ \begin{aligned} & \text { Apabila } H=4, M=81 \\ & \begin{aligned} G & =1.5(4)(\sqrt{81}) \\ & =54 \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Apabila } G=18, H=20\\ &\begin{aligned} 18 & =1.5(20)(\sqrt{M}) \\ \sqrt{M} & =\frac{18}{(1.5)(20)} \\ \sqrt{M} & =0.6 \\ M & =0.6^2 \\ M & =0.36 \end{aligned} \end{aligned} $$
Soalan 6:
Jadual di bawah menunjukkan perubahan tiga kuantiti. Diberi P berubah secara langsung dengan kuasa tiga Q, dan R. Hitung nilai x dan nilai y.
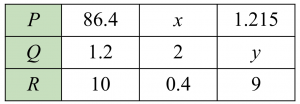
Penyelesaian:
$$ \text { Diberi } P=86.4, Q=1.2, R=10 $$
$$ \begin{aligned} &\begin{aligned} P & \propto Q^3 R \\ P & =k Q^3 R \\ 86.4 & =k(1.23)(10) \\ k & =\frac{86.4}{\left(1.2^3\right)(10)} \\ k & =5 \end{aligned}\\ &\text { Maka } P=5 Q^3 R \end{aligned} $$
$$ \begin{aligned} & \text { Apabila } P=x, Q=2, R=0.4 \\ & x=5\left(2^3\right)(0.4) \\ & x=16 \end{aligned} $$
$$ \begin{aligned} & \text { Apabila } P=1.215, Q=y, R=9 \\ & 1.215=5\left(y^3\right)(9) \\ & y^3=\frac{1.215}{(5)(9)} \\ & y^3=0.027 \\ & y=0.3 \end{aligned} $$
Jadual di bawah menunjukkan perubahan tiga kuantiti. Diberi P berubah secara langsung dengan kuasa tiga Q, dan R. Hitung nilai x dan nilai y.

Penyelesaian:
$$ \text { Diberi } P=86.4, Q=1.2, R=10 $$
$$ \begin{aligned} &\begin{aligned} P & \propto Q^3 R \\ P & =k Q^3 R \\ 86.4 & =k(1.23)(10) \\ k & =\frac{86.4}{\left(1.2^3\right)(10)} \\ k & =5 \end{aligned}\\ &\text { Maka } P=5 Q^3 R \end{aligned} $$
$$ \begin{aligned} & \text { Apabila } P=x, Q=2, R=0.4 \\ & x=5\left(2^3\right)(0.4) \\ & x=16 \end{aligned} $$
$$ \begin{aligned} & \text { Apabila } P=1.215, Q=y, R=9 \\ & 1.215=5\left(y^3\right)(9) \\ & y^3=\frac{1.215}{(5)(9)} \\ & y^3=0.027 \\ & y=0.3 \end{aligned} $$
Soalan 7:
Tenaga kinetik, E Joule, sebuah objek berubah secara langsung dengan jisim, w kg dan kuasa dua laju, v m s–1, objek itu. Diberi bahawa tenaga kinetik sebuah objek dengan jisim 3 kg bergerak dengan kelajuan 12 m s–1 ialah 216 Joule. Hitung laju dalam m s–1, objek itu jika jisim dan tenaga kinetik masing-masing ialah 5 kg dan 640 Joule.
Penyelesaian:
$$ \begin{aligned} & E \alpha w v^2 \\ & E=k w v^2 \end{aligned} $$
$$ \begin{aligned} \text { Apabila } w & =3, v=12, E=216 \\ 216 & =k(3)\left(12^2\right) \\ k & =\frac{216}{(3)\left(12^2\right)} \\ k & =0.5 \\ \text { Maka } E & =0.5 w v^2 \end{aligned} $$
$$ \begin{aligned} \text { Apabila } w & =5, E=640 \\ 640 & =0.5(5) v^2 \\ v^2 & =\frac{640}{(0.5)(5)} \\ v^2 & =256 \\ v & =16 \mathrm{~ms}^{-1} \end{aligned} $$
Tenaga kinetik, E Joule, sebuah objek berubah secara langsung dengan jisim, w kg dan kuasa dua laju, v m s–1, objek itu. Diberi bahawa tenaga kinetik sebuah objek dengan jisim 3 kg bergerak dengan kelajuan 12 m s–1 ialah 216 Joule. Hitung laju dalam m s–1, objek itu jika jisim dan tenaga kinetik masing-masing ialah 5 kg dan 640 Joule.
Penyelesaian:
$$ \begin{aligned} & E \alpha w v^2 \\ & E=k w v^2 \end{aligned} $$
$$ \begin{aligned} \text { Apabila } w & =3, v=12, E=216 \\ 216 & =k(3)\left(12^2\right) \\ k & =\frac{216}{(3)\left(12^2\right)} \\ k & =0.5 \\ \text { Maka } E & =0.5 w v^2 \end{aligned} $$
$$ \begin{aligned} \text { Apabila } w & =5, E=640 \\ 640 & =0.5(5) v^2 \\ v^2 & =\frac{640}{(0.5)(5)} \\ v^2 & =256 \\ v & =16 \mathrm{~ms}^{-1} \end{aligned} $$
Soalan 8:
Isi padu sebuah kon, V cm3, berubah secara langsung dengan tinggi, h cm, dan kuasa dua jejari tapaknya, j cm. Sebuah kon dengan tinggi 21 cm dan jejari 6 cm mempunyai isi padu 792 cm3. Hitung isi padu dalam cm3, kon dengan tinggi 14 cm dan jejari 15 cm.
Penyelesaian:
$$ \begin{gathered} v \alpha h j^2 \\ v=k h j^2 \end{gathered} $$
$$ \begin{aligned} \text { Apabila } h & =21, j=6, v=792 \\ 792 & =k(21)\left(6^2\right) \\ k & =\frac{792}{(21)\left(6^2\right)} \\ k & =\frac{22}{21} \\ \text { Maka } v & =\frac{22}{21} h j^2 \end{aligned} $$
$$ \begin{aligned} & \text { Apabila } h=14, j=15 \\ & \qquad \begin{aligned} v & =\frac{22}{21}(14)\left(15^2\right) \\ & =3300 \mathrm{~cm}^3 \end{aligned} \end{aligned} $$
Isi padu sebuah kon, V cm3, berubah secara langsung dengan tinggi, h cm, dan kuasa dua jejari tapaknya, j cm. Sebuah kon dengan tinggi 21 cm dan jejari 6 cm mempunyai isi padu 792 cm3. Hitung isi padu dalam cm3, kon dengan tinggi 14 cm dan jejari 15 cm.
Penyelesaian:
$$ \begin{gathered} v \alpha h j^2 \\ v=k h j^2 \end{gathered} $$
$$ \begin{aligned} \text { Apabila } h & =21, j=6, v=792 \\ 792 & =k(21)\left(6^2\right) \\ k & =\frac{792}{(21)\left(6^2\right)} \\ k & =\frac{22}{21} \\ \text { Maka } v & =\frac{22}{21} h j^2 \end{aligned} $$
$$ \begin{aligned} & \text { Apabila } h=14, j=15 \\ & \qquad \begin{aligned} v & =\frac{22}{21}(14)\left(15^2\right) \\ & =3300 \mathrm{~cm}^3 \end{aligned} \end{aligned} $$