Soalan 1:
Lee mengisi air ke dalam sebuah tangki dengan menggunakan hos getah pada pukul 8:00 pagi. Pada pukul 11:00 pagi, Lee mendapati bahawa tangki itu telah diisi dengan 48% air.
(a) Tuliskan satu persamaan yang menghubungkan isi padu air, V, yang diisi ke dalam tangki dengan masa yang diambil, t.
(b) Pada pukul berapakah tangki itu akan diisi penuh dengan air?
Penyelesaian:
(a)
$$ \begin{gathered} v \alpha t \\ v=k t \\ \text { Diberi } t=3 \text { jam, } v=48 \%=0.48 \\ 0.48=k(3) \\ k=\frac{0.48}{3} \\ k=0.16 \end{gathered} $$
(b)
$$ \begin{aligned} \text { Diberi } v & =100 \%=1 \\ v & =0.16 t \\ 1 & =0.16 t \\ t & =\frac{1}{0.16} \\ & =6.25 \text { jam } \\ & =6 \text { jam }(0.25 \times 60) \text { minit } \\ & =6 \text { jam } 15 \text { minit } \end{aligned} $$

$$ \begin{aligned} &\text { Tangki akan penuh pada }\\ &\begin{aligned} & =8.00 \text { pagi }+6 \text { jam } 15 \text { minit } \\ & =2: 15 \text { petang } \end{aligned} \end{aligned} $$
Lee mengisi air ke dalam sebuah tangki dengan menggunakan hos getah pada pukul 8:00 pagi. Pada pukul 11:00 pagi, Lee mendapati bahawa tangki itu telah diisi dengan 48% air.
(a) Tuliskan satu persamaan yang menghubungkan isi padu air, V, yang diisi ke dalam tangki dengan masa yang diambil, t.
(b) Pada pukul berapakah tangki itu akan diisi penuh dengan air?
Penyelesaian:
(a)
$$ \begin{gathered} v \alpha t \\ v=k t \\ \text { Diberi } t=3 \text { jam, } v=48 \%=0.48 \\ 0.48=k(3) \\ k=\frac{0.48}{3} \\ k=0.16 \end{gathered} $$
(b)
$$ \begin{aligned} \text { Diberi } v & =100 \%=1 \\ v & =0.16 t \\ 1 & =0.16 t \\ t & =\frac{1}{0.16} \\ & =6.25 \text { jam } \\ & =6 \text { jam }(0.25 \times 60) \text { minit } \\ & =6 \text { jam } 15 \text { minit } \end{aligned} $$

$$ \begin{aligned} &\text { Tangki akan penuh pada }\\ &\begin{aligned} & =8.00 \text { pagi }+6 \text { jam } 15 \text { minit } \\ & =2: 15 \text { petang } \end{aligned} \end{aligned} $$
Soalan 2:
Aminah ingin menggunting beberapa bentuk segi tiga daripada sekeping kad. Diberi luas segi tiga yang digunting, L cm2, berubah secara langsung dengan tapak, x cm, dan tinggi, y cm. Pada mulanya, dia menggunting satu segi tiga dengan L = 14, x = 7 dan y = 4.
(a) Tuliskan hubungan antara L dengan x dan y.
(b) Aminah merancang untuk menggunting segi tiga kedua dengan nilai tapak bertambah 20% dan nilai tinggi berkurang 10%. Berapakah peratusan perubahan untuk luas segi tiga kedua ini?
Penyelesaian:
(a)
$$ \begin{aligned} &\begin{aligned} & L \alpha x y \\ & L=k x y \end{aligned}\\ &\begin{aligned} & \text { Diberi } L=14, x=7, y=4 \\ & \qquad \begin{array}{l} 14=k(7)(4) \\ k=\frac{14}{7(4)} \\ k=0.5 \end{array} \end{aligned}\\ &\text { Maka } L=0.5 x y \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Tapak bertambah + 20%, }\\ &\begin{aligned} x & =7+7(0.2) \\ & =8.4 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Tinggi berkurang – 10% }\\ &\begin{aligned} y & =4-4(0.1) \\ & =3.6 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Luas segi tiga kedua, }\\ &\begin{aligned} L_2 & =0.5(8.4)(3.6) \\ & =15.12 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Peratusan perubahan luas segi tiga kedua }\\ &\begin{aligned} & =\frac{15.12-14}{14} \times 100 \% \\ & =8 \% \end{aligned} \end{aligned} $$
$$ \text { Maka, luas segi tiga kedua bertambah } 8 \text {%. } $$
Aminah ingin menggunting beberapa bentuk segi tiga daripada sekeping kad. Diberi luas segi tiga yang digunting, L cm2, berubah secara langsung dengan tapak, x cm, dan tinggi, y cm. Pada mulanya, dia menggunting satu segi tiga dengan L = 14, x = 7 dan y = 4.
(a) Tuliskan hubungan antara L dengan x dan y.
(b) Aminah merancang untuk menggunting segi tiga kedua dengan nilai tapak bertambah 20% dan nilai tinggi berkurang 10%. Berapakah peratusan perubahan untuk luas segi tiga kedua ini?
Penyelesaian:
(a)
$$ \begin{aligned} &\begin{aligned} & L \alpha x y \\ & L=k x y \end{aligned}\\ &\begin{aligned} & \text { Diberi } L=14, x=7, y=4 \\ & \qquad \begin{array}{l} 14=k(7)(4) \\ k=\frac{14}{7(4)} \\ k=0.5 \end{array} \end{aligned}\\ &\text { Maka } L=0.5 x y \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Tapak bertambah + 20%, }\\ &\begin{aligned} x & =7+7(0.2) \\ & =8.4 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Tinggi berkurang – 10% }\\ &\begin{aligned} y & =4-4(0.1) \\ & =3.6 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Luas segi tiga kedua, }\\ &\begin{aligned} L_2 & =0.5(8.4)(3.6) \\ & =15.12 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Peratusan perubahan luas segi tiga kedua }\\ &\begin{aligned} & =\frac{15.12-14}{14} \times 100 \% \\ & =8 \% \end{aligned} \end{aligned} $$
$$ \text { Maka, luas segi tiga kedua bertambah } 8 \text {%. } $$
Soalan 3:
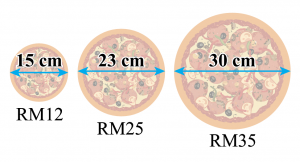
Sebuah kedai piza menjual tiga saiz piza dengan harga berbeza seperti yang ditunjukkan dalam rajah di sebelah. Adakah harga piza, RMp, berubah secara langsung dengan luas permukaan, A cm2, piza itu? Jika tidak, saiz piza yang manakah lebih berbaloi dengan harganya?
Penyelesaian:
$$ \begin{aligned} & \text { Luas bulatan }=\pi j^2 \\ & \begin{aligned} \text { Luas piza RM } 12 & =\frac{22}{7} \times\left(\frac{15}{2}\right)^2 \\ & =176.79 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Luas piza RM } 25 & =\frac{22}{7} \times\left(\frac{23}{2}\right)^2 \\ & =415.64 \mathrm{~cm}^2 \end{aligned} $$
$$ \begin{aligned} \text { Luas piza RM } 35= & \frac{22}{7} \times\left(\frac{30}{2}\right)^2 \\ & =707.14 \mathrm{~cm}^2 \end{aligned} $$
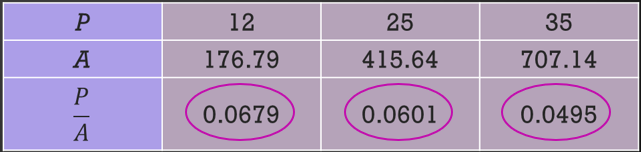

Sebuah kedai piza menjual tiga saiz piza dengan harga berbeza seperti yang ditunjukkan dalam rajah di sebelah. Adakah harga piza, RMp, berubah secara langsung dengan luas permukaan, A cm2, piza itu? Jika tidak, saiz piza yang manakah lebih berbaloi dengan harganya?
Penyelesaian:
$$ \begin{aligned} & \text { Luas bulatan }=\pi j^2 \\ & \begin{aligned} \text { Luas piza RM } 12 & =\frac{22}{7} \times\left(\frac{15}{2}\right)^2 \\ & =176.79 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Luas piza RM } 25 & =\frac{22}{7} \times\left(\frac{23}{2}\right)^2 \\ & =415.64 \mathrm{~cm}^2 \end{aligned} $$
$$ \begin{aligned} \text { Luas piza RM } 35= & \frac{22}{7} \times\left(\frac{30}{2}\right)^2 \\ & =707.14 \mathrm{~cm}^2 \end{aligned} $$

Harga piza tidak berubah secara langsung dengan luas permukaan.
Piza dengan diameter 30 cm lebih berbaloi dengan harganya.