Soalan 6:
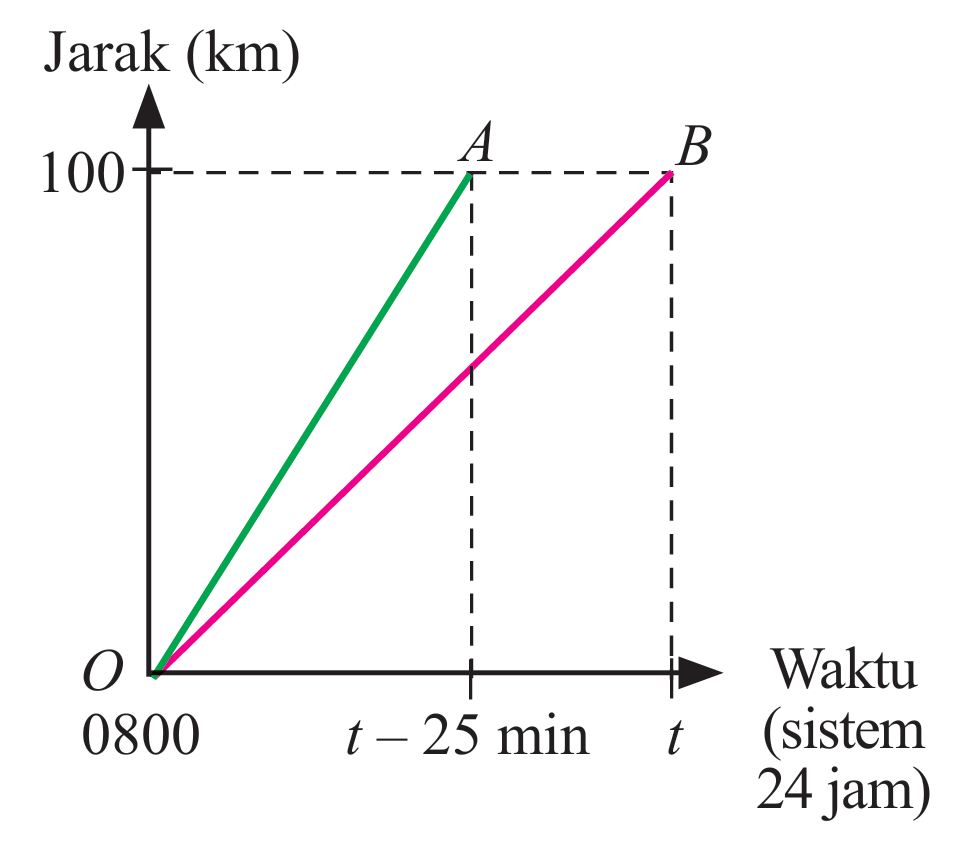
Graf jarak-masa di sebelah menunjukkan gerakan dua buah kereta sejauh 100 km. Graf OA menunjukkan gerakan kereta yang dipandu oleh Encik Lee dengan laju purata v km j–1 dan graf OB ialah gerakan kereta yang dipandu oleh Encik Dollah dengan laju purata (v – 20) km j–1. Hitung,
(a) nilai v jika beza masa yang diambil oleh Encik Lee dan Encik Dollah untuk sampai di destinasi ialah 25 minit.
(b) waktu, dalam sistem 24 jam Encik Lee sampai di destinasinya.
Penyelesaian:
(a)
$$ \begin{array}{rl} \text { Masa } & =\frac{\text { Jarak }}{\text { Laju }} \\ \frac{100}{v}-\frac{100}{v-20} & =\frac{25}{60} \\ \frac{100(v-20)-100 v}{v(v-20)} & =\frac{5}{12} \\ \frac{100 v-2000-100 v}{v^2-20 v} & =\frac{5}{12} \\ -24000 & =5 v^2-100 v \\ v^2-20 v-4800 & =0 \\ (v-80)(v+60) & =0 \\ v-80=0 & \text { atau } \quad v+60=0 \\ v=80 & v=-60 \text { (ditolak) } \end{array} $$
(b)
$$ \begin{aligned} &\text { Laju purata Encik Dollah }=80-20=60 \mathrm{~km} \mathrm{j}^{-1}\\ &\begin{aligned} \frac{100}{t} & =60 \\ 60 t & =100 \\ t & =\frac{100}{60} \\ t & =\frac{5}{3} j a m \\ \frac{5}{3} j a m \times 60 & =100 \text { minit } \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Waktu Encik Lee sampai di destinasi }\\ &\begin{aligned} & =0800+(100-25) \\ & =0800+75 \\ & =0800+60+15 \\ & =\text { Jam } 0915 \end{aligned} \end{aligned} $$

Graf jarak-masa di sebelah menunjukkan gerakan dua buah kereta sejauh 100 km. Graf OA menunjukkan gerakan kereta yang dipandu oleh Encik Lee dengan laju purata v km j–1 dan graf OB ialah gerakan kereta yang dipandu oleh Encik Dollah dengan laju purata (v – 20) km j–1. Hitung,
(a) nilai v jika beza masa yang diambil oleh Encik Lee dan Encik Dollah untuk sampai di destinasi ialah 25 minit.
(b) waktu, dalam sistem 24 jam Encik Lee sampai di destinasinya.
Penyelesaian:
(a)
$$ \begin{array}{rl} \text { Masa } & =\frac{\text { Jarak }}{\text { Laju }} \\ \frac{100}{v}-\frac{100}{v-20} & =\frac{25}{60} \\ \frac{100(v-20)-100 v}{v(v-20)} & =\frac{5}{12} \\ \frac{100 v-2000-100 v}{v^2-20 v} & =\frac{5}{12} \\ -24000 & =5 v^2-100 v \\ v^2-20 v-4800 & =0 \\ (v-80)(v+60) & =0 \\ v-80=0 & \text { atau } \quad v+60=0 \\ v=80 & v=-60 \text { (ditolak) } \end{array} $$
(b)
$$ \begin{aligned} &\text { Laju purata Encik Dollah }=80-20=60 \mathrm{~km} \mathrm{j}^{-1}\\ &\begin{aligned} \frac{100}{t} & =60 \\ 60 t & =100 \\ t & =\frac{100}{60} \\ t & =\frac{5}{3} j a m \\ \frac{5}{3} j a m \times 60 & =100 \text { minit } \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Waktu Encik Lee sampai di destinasi }\\ &\begin{aligned} & =0800+(100-25) \\ & =0800+75 \\ & =0800+60+15 \\ & =\text { Jam } 0915 \end{aligned} \end{aligned} $$
Soalan 7:
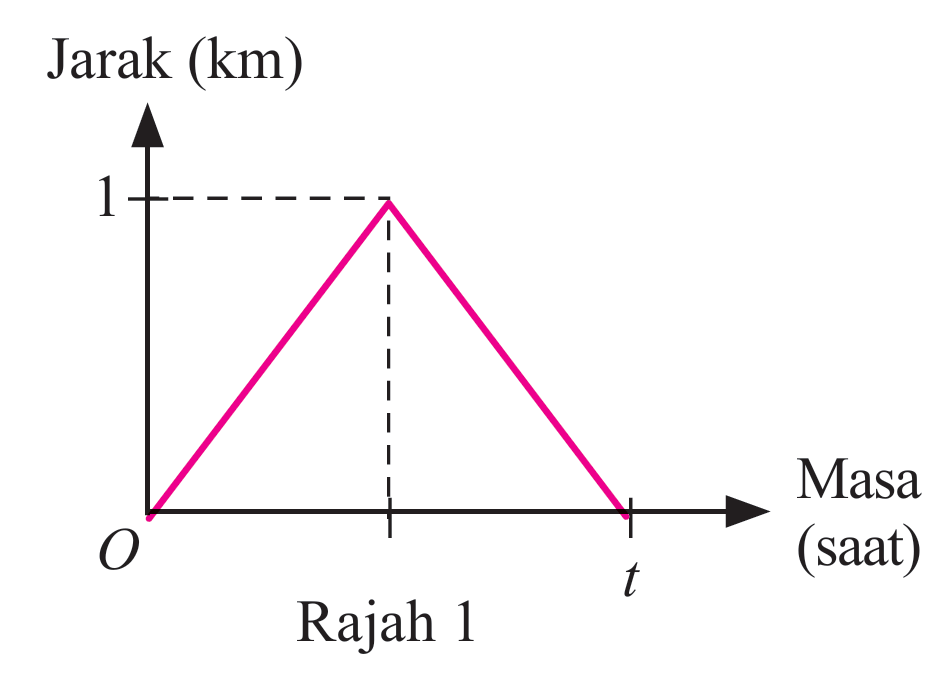
(a)(i) Rajah 1 menunjukkan graf jarak-masa kereta A untuk tempoh t saat. Diberi laju purata kereta A ialah 25 ms–1. Hitung nilai t.
(ii) Huraikan gerakan kereta A untuk tempoh t saat.
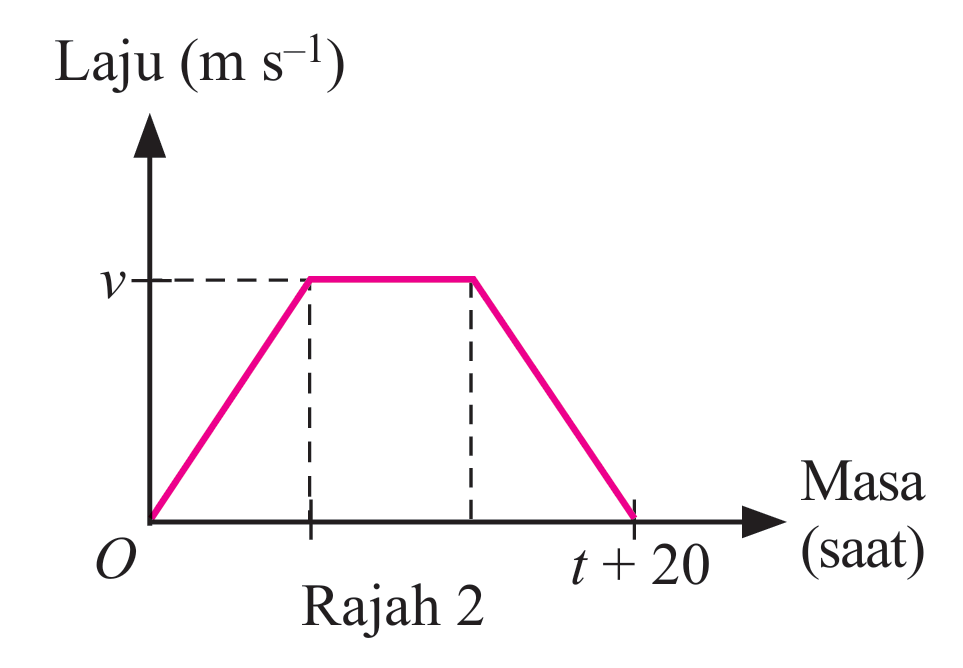
(b) Rajah 2 menunjukkan graf laju-masa kereta B. Diberi bahawa, laju seragam, v, kereta B adalah sama dengan laju purata kereta A dan jarak yang dilalui oleh kedua-dua buah kereta adalah sama. Jika nilai t, dalam saat untuk kedua-dua graf adalah sama, hitung tempoh masa, dalam minit, kereta B bergerak dengan laju seragam.
Penyelesaian:
(a)(i)
$$ \begin{aligned} \text { Jarak yang didalui oleh kereta } A & =1+1 \\ & =2 \mathrm{~km} \\ & =2000 \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} \text { Laju purata } & =\frac{\text { Jarak }}{\text { Masa }} \\ 25 & =\frac{2000}{t} \\ t & =\frac{2000}{25} \\ t & =80 \end{aligned} $$
(a)(ii)
Kereta A bergerak dengan laju purata 25 ms-1 sejauh 2 km dalam tempoh 80 saat.
(b)
Katakan a adalah tempoh masa apabila kereta B bergerak dengan laju seragam.
$$ \begin{aligned} \frac{1}{2}[a+(t+20)](25) & =2000 \\ {[a+(80+20)](25) } & =4000 \\ 25 a+2500 & =4000 \\ 25 a & =1500 \\ a & =60 \\ a & =1 \text { minit } \end{aligned} $$

(a)(i) Rajah 1 menunjukkan graf jarak-masa kereta A untuk tempoh t saat. Diberi laju purata kereta A ialah 25 ms–1. Hitung nilai t.
(ii) Huraikan gerakan kereta A untuk tempoh t saat.

(b) Rajah 2 menunjukkan graf laju-masa kereta B. Diberi bahawa, laju seragam, v, kereta B adalah sama dengan laju purata kereta A dan jarak yang dilalui oleh kedua-dua buah kereta adalah sama. Jika nilai t, dalam saat untuk kedua-dua graf adalah sama, hitung tempoh masa, dalam minit, kereta B bergerak dengan laju seragam.
Penyelesaian:
(a)(i)
$$ \begin{aligned} \text { Jarak yang didalui oleh kereta } A & =1+1 \\ & =2 \mathrm{~km} \\ & =2000 \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} \text { Laju purata } & =\frac{\text { Jarak }}{\text { Masa }} \\ 25 & =\frac{2000}{t} \\ t & =\frac{2000}{25} \\ t & =80 \end{aligned} $$
(a)(ii)
Kereta A bergerak dengan laju purata 25 ms-1 sejauh 2 km dalam tempoh 80 saat.
(b)
Katakan a adalah tempoh masa apabila kereta B bergerak dengan laju seragam.
$$ \begin{aligned} \frac{1}{2}[a+(t+20)](25) & =2000 \\ {[a+(80+20)](25) } & =4000 \\ 25 a+2500 & =4000 \\ 25 a & =1500 \\ a & =60 \\ a & =1 \text { minit } \end{aligned} $$