(a) Diberi kos θ∘ = -0.5150 dan 90∘ ≤ θ ≤ 270∘, hitung nilai θ. [2 markah]
(b)(i) Pada Rajah 2 di ruang jawapan, lakarkan graf y = 1.5 kos 2x – 1 dengan keadaan 0∘ ≤ θ ≤ 360∘. [2 markah]
(b)(ii) Berdasarkan graf yang telah dilukis, nyatakan kesan perubahan graf apabila diberi nilai amplitud adalah 3. [1 markah]
Penyelesaian:
(a)
kos θ∘ = -0.5150 ⇐ Tanda negatif. θ berada dalam sukuan II atau III.
Sudut rujukan sepadan,
α = kos-1 0.5150
= 59∘
Sukuan II
θ = 180∘ – 59∘
= 121∘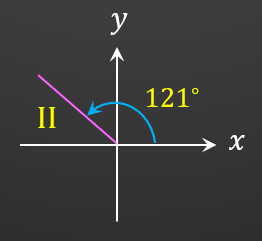
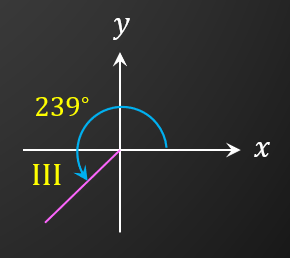
Sukuan III
θ = 180∘ + 59∘
= 239∘
(b)(i)
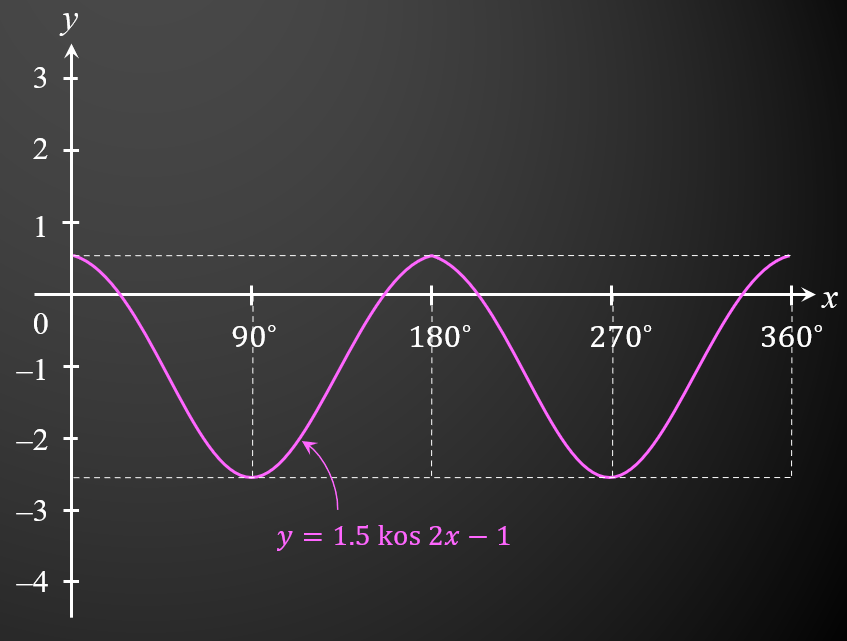
(b)(ii)
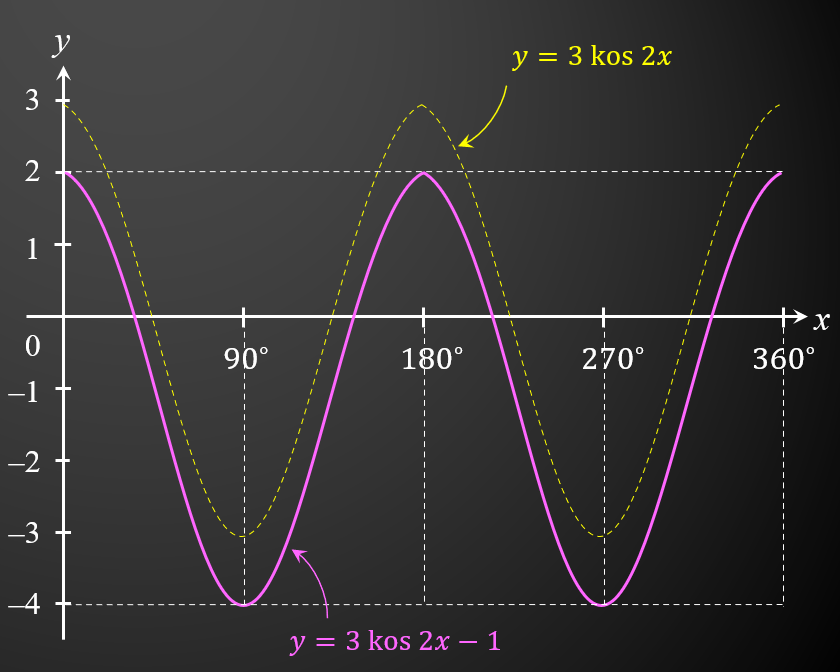
Apabila nilai amplitud adalah 3, titik maksimum akan berada pada y = 2 dan titik minimum akan berada pada y = -4.
$$
\text { (a) Transformasi } \mathbf{M} \text { mewakili translasi }\binom{7}{-2} \text {. }
$$
Transformasi N mewakili pantulan pada garis y = x.
Nyatakan koordinat imej bagi titik (1, 4) di bawah gabungan transformasi NM. [2 markah]
(b) Rajah 3 menunjukkan dua bentuk geometri, dilukis pada suatu satah Cartes.

(i) Nyatakan sama ada heksagon L dan heksagon K adalah kongruen. Justifikasikan jawapan anda. [1 markah]
(ii) Heksagon L ialah imej bagi heksagon K di bawah satu transformasi Q. Huraikan selengkapnya transformasi Q. [2 markah]
Penyelesaian:
(a)
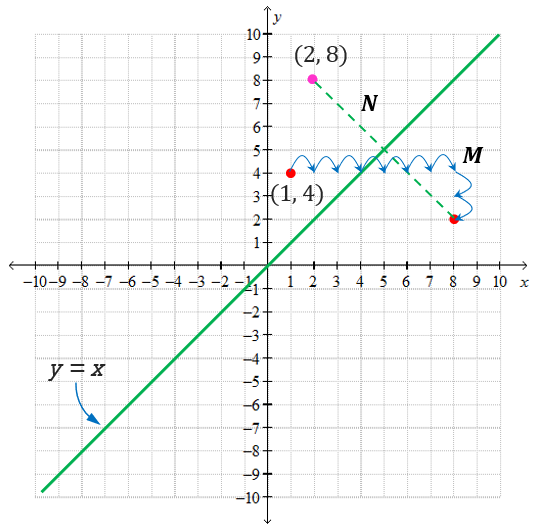
Koordinat imej bagi titik (1, 4) di bawah gabungan transformasi NM ialah (2, 8).
(b)(i)
Ya kerana ukuran semua panjang sisi adalah sepadan dan semua sudut adalah sepadan bagi kedua-dua hekasagon.
(b)(ii)
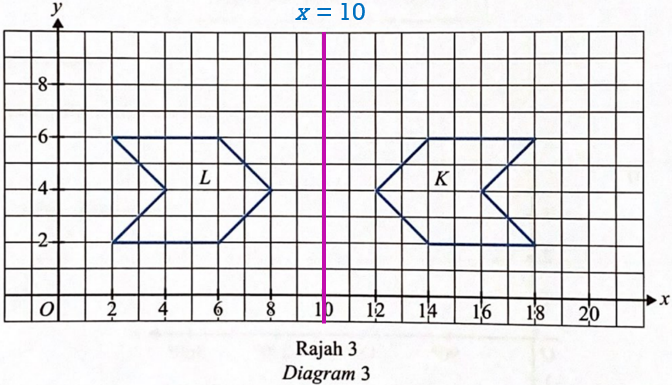
Transformasi Q adalah pantulan pada paksi x = 10.