Soalan 7:
(a) Rajah 4 menunjukkan langkah-langkah dalam proses pengurusan kewangan yang tidak lengkap.
(b) Jadual 2 menunjukkan pendapatan dan perbelanjaan Amelia dan Julia bagi bulan Januari.
$$
\begin{aligned}
&\text { Kedudukan kewangan Julia }\\
&\begin{aligned}
& =\text { RM }(3000+150+850)-R M(1800+700+300) \\
& =\text { RM4 } 000+\text { RM2 } 800 \\
& =\text { RM1 } 200
\end{aligned}
\end{aligned}
$$
Amelia mempunyai kedudukan kewangan yang lebih baik kerana pendapatan lebihan Amelia adalah lebih banyak berbanding Julia.
(a) Rajah 4 menunjukkan langkah-langkah dalam proses pengurusan kewangan yang tidak lengkap.
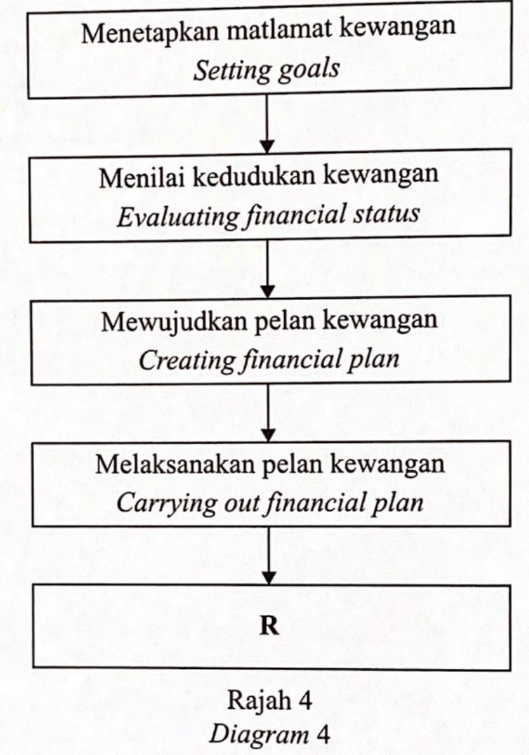
Nyatakan Langkah yang berlabel R. [1 markah]
(b) Jadual 2 menunjukkan pendapatan dan perbelanjaan Amelia dan Julia bagi bulan Januari.

Antara Amelia dan Julia, siapakah mempunyai kedudukan kewangan yang lebih baik? Justifikasikan jawapan anda. [3 markah]
Penyelesaian:
(a) Mengkaji semula dan menyemak kemajuan
(b)
Pendapatan = gaji bersih, komisen jualan, sewa yang diterima
Perbelanjaan = pinjaman perumahan, bil utility dan premium insurans
$$
\begin{aligned}
&\text { Kedudukan kewangan Amelia }\\
&\begin{aligned}
& =\mathrm{RM}(3500+400+800)-\mathrm{RM}(1300+650+200) \\
& =\text { RM4 } 700+\mathrm{RM} 2150 \\
& =\text { RM2 } 550
\end{aligned}
\end{aligned}
$$
$$
\begin{aligned}
&\text { Kedudukan kewangan Julia }\\
&\begin{aligned}
& =\text { RM }(3000+150+850)-R M(1800+700+300) \\
& =\text { RM4 } 000+\text { RM2 } 800 \\
& =\text { RM1 } 200
\end{aligned}
\end{aligned}
$$
Amelia mempunyai kedudukan kewangan yang lebih baik kerana pendapatan lebihan Amelia adalah lebih banyak berbanding Julia.
Soalan 8:
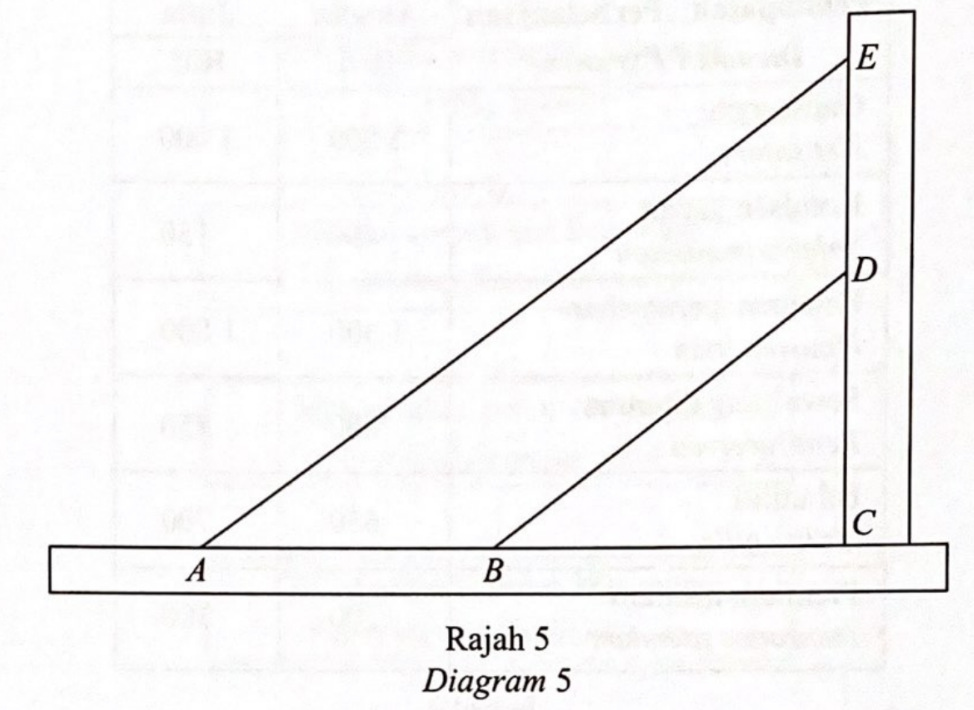
Rajah 5 menunjukkan dua utas tali AE dan BD yang diikat secara selari pada sebatang tiang kayu yang tegak EC.
Diberi persamaan garis lurus BD ialah 4y – 3x = 48 dan nisbah jarak AB : BC ialah 3 : 4.
Cari,
(a) persamaan garis lurus AE, [3 markah]
(b) jarak ED. [1 markah]
Penyelesaian:
(a)
$$
\begin{aligned}
&\text { Pada titik E, koordinat } y=0\\
&\begin{aligned}
4(0)-3 x & =48 \\
x & =-\frac{48}{3} \\
x & =-16
\end{aligned}
\end{aligned}
$$
$$
\text { Diberi } \begin{aligned}
\frac{A B}{B C} & =\frac{3}{4} \\
\frac{A B}{16} & =\frac{3}{4} \\
A B & =\frac{16 \times 3}{4} \\
A B & =12
\end{aligned}
$$
$$
\begin{aligned}
&\text { Maka koordinat titik } A\\
&\begin{aligned}
& =(-16-12), 0) \\
& =(-28,0)
\end{aligned}
\end{aligned}
$$
$$
\begin{aligned}
4 y-3 x & =48 \\
y & =\frac{3}{4} x+\frac{48}{4} \\
y & =\frac{3}{4} x+12 \\
m & =\frac{3}{4}
\end{aligned}
$$
$$
\begin{aligned}
& m_{A E}=m_{B D}=\frac{3}{4} \\
& y=\frac{3}{4} x+c,(-28,0) \\
& 0=\frac{3}{4}(-28)+c \\
& c=21
\end{aligned}
$$
$$
\begin{aligned}
&\text { Persamaan garis lurus } A E \text {, }\\
&y=\frac{3}{4} x+21
\end{aligned}
$$
(b)
$$
\text { Pintasan } y \text { bagi persamaan, } y=\frac{3}{4} x+12 \text { adalah } 12
$$
$$
\text { Maka, titik } D=(0,12)
$$
$$
\text { Pintasan } y \text { bagi persamaan, } y=\frac{3}{4} x+21 \text { adalah } 21
$$
$$
\text { Maka, titik } E=(0,21)
$$
$$
\begin{aligned}
\text { Jarak } E D & =21-12 \\
& =9 \text { units }
\end{aligned}
$$
Rajah 5 menunjukkan dua utas tali AE dan BD yang diikat secara selari pada sebatang tiang kayu yang tegak EC.
Diberi persamaan garis lurus BD ialah 4y – 3x = 48 dan nisbah jarak AB : BC ialah 3 : 4.
Cari,

(a) persamaan garis lurus AE, [3 markah]
(b) jarak ED. [1 markah]
Penyelesaian:
(a)
$$
\begin{aligned}
&\text { Pada titik E, koordinat } y=0\\
&\begin{aligned}
4(0)-3 x & =48 \\
x & =-\frac{48}{3} \\
x & =-16
\end{aligned}
\end{aligned}
$$
$$
\text { Diberi } \begin{aligned}
\frac{A B}{B C} & =\frac{3}{4} \\
\frac{A B}{16} & =\frac{3}{4} \\
A B & =\frac{16 \times 3}{4} \\
A B & =12
\end{aligned}
$$
$$
\begin{aligned}
&\text { Maka koordinat titik } A\\
&\begin{aligned}
& =(-16-12), 0) \\
& =(-28,0)
\end{aligned}
\end{aligned}
$$
$$
\begin{aligned}
4 y-3 x & =48 \\
y & =\frac{3}{4} x+\frac{48}{4} \\
y & =\frac{3}{4} x+12 \\
m & =\frac{3}{4}
\end{aligned}
$$
$$
\begin{aligned}
& m_{A E}=m_{B D}=\frac{3}{4} \\
& y=\frac{3}{4} x+c,(-28,0) \\
& 0=\frac{3}{4}(-28)+c \\
& c=21
\end{aligned}
$$
$$
\begin{aligned}
&\text { Persamaan garis lurus } A E \text {, }\\
&y=\frac{3}{4} x+21
\end{aligned}
$$
(b)
$$
\text { Pintasan } y \text { bagi persamaan, } y=\frac{3}{4} x+12 \text { adalah } 12
$$
$$
\text { Maka, titik } D=(0,12)
$$
$$
\text { Pintasan } y \text { bagi persamaan, } y=\frac{3}{4} x+21 \text { adalah } 21
$$
$$
\text { Maka, titik } E=(0,21)
$$
$$
\begin{aligned}
\text { Jarak } E D & =21-12 \\
& =9 \text { units }
\end{aligned}
$$