Soalan Percubaan Matematik SPM 2021 (Kelantan), Kertas 2 – Soalan 1 & 2

                                                         Bahagian A
                                                          40 markah
                                                 Jawap semua soalan

Soalan 1 (4 markah):
Rajah 1 menunjukkan suatu satah Cartesan.
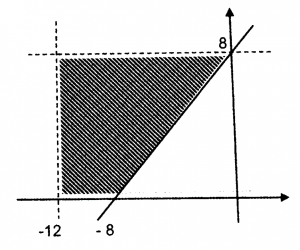Rajah 1
Tulis empat ketaksamaan yang mentakrifkan rantau yang berlorek.

Jawapan:
(i)
(ii)
(iii)
(iv)

Penyelesaian:

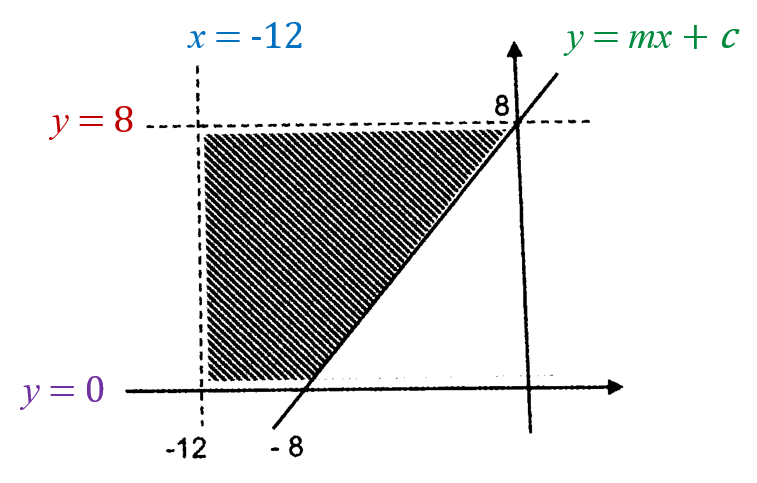
(i)
Bagi y = 8
Ketaksamaan bagi rantau di bawah graf garis sempang ialah y < 8.


(ii)
Bagi x = -12
Ketaksamaan bagi rantau di sebelah kanan graf garis sempang ialah x > -12.

(iii)
Bagi y = 0
Ketaksamaan bagi rantau di atas paksi x ialah y ≥ 0.

(iv)
$\begin{array}{l}y=mx+c\\ c=8\\ \\ m=-\frac{8}{-8}=1\\ \therefore y=x+8\end{array}$

Ketaksamaan bagi rantau di atas graf garis padu ialah y ≥ x + 8.

Soalan 2 (4 markah):
Diberi luas segi tiga, A, berubah secara langsung dengan pemalar, k, dengan tinggi, x cm dan tapak, y cm. Rajoo mempunyai sekeping kadbod berbentuk segi tiga dengan x dan y masing-masing  80 cm dan 48 cm. Hitung nilai k jika luas kadbod itu ialah 15 360 cm². Seterusnya, hitung nilai A jika Rajoo mempunyai sekeping lagi kadbod dengan jumlah  x dan y ialah 180 cm di mana nisbah x kepada y ialah 5 : 4.

Penyelesaian:
A α xy
A = kxy

A = 15 360, x = 80, y = 48
15 360 = k × 80 × 48
15 360 = 3 840 k 
k = 4

x + y = 180
x : y = 5 : 4

$\begin{array}{l}x=\frac{\text{5}}{\text{9}}\times 180\\ =100\\ \\ y=\frac{\text{4}}{\text{9}}\times 180\\ =80\\ \\ \therefore A=4\times 100\times 80\\ =32000\end{array}$