6.1.2 Nilai Sinus, Kosinus dan Tangen bagi Sesuatu Sudut (Bahagian 2)
(D) Sudut khusus 30o, 45o, 60o
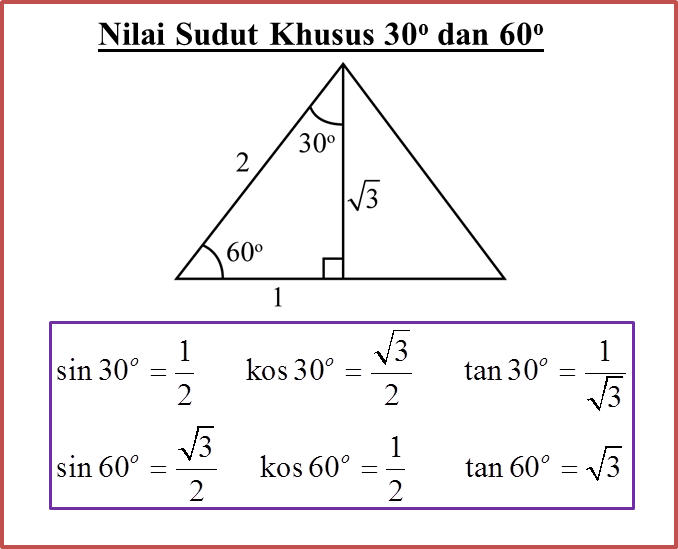
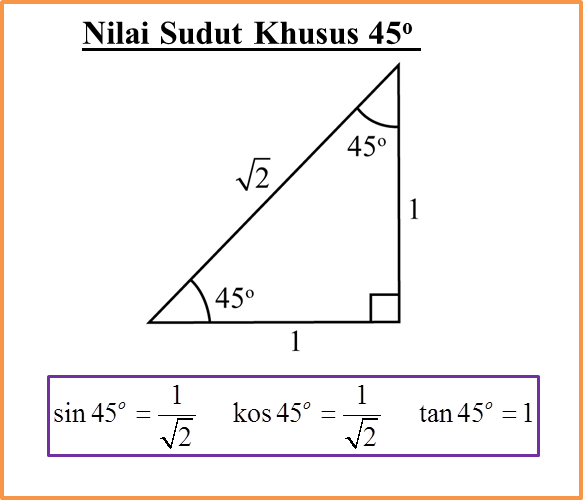
(E) Mencari sudut di antara 0o dengan 360o apabila nilai sin θ, kos θ atau tan θ diberi
1. Jika nilai sin θ, kos θ atau tan θ diberi dan 0o< θ < 360o, nilai θ dapat dicari dengan menggunakan langkah-langkah di bawah.
(a) Cari sudut asas dalam sukuan I yang sesuai dengan θ.
(b) Berdasarkan nilai (positif atau negatif) bagi sin θ, kos θ atau tan θ, tentukan sukuan yang mana θ berada.
(c) Cari nilai-nilai θ dalam sukuan yang dicari dalam (b).
(a) Cari sudut asas dalam sukuan I yang sesuai dengan θ.
(b) Berdasarkan nilai (positif atau negatif) bagi sin θ, kos θ atau tan θ, tentukan sukuan yang mana θ berada.
(c) Cari nilai-nilai θ dalam sukuan yang dicari dalam (b).
Contoh:
Cari nilai θ yang memuaskan setiap persamaan di bawah.
(a) sin θ = 0.6025 dan 90o < θ < 180o
(b) kos θ = –0.6025 dan 180o < θ < 270o
(c) sin θ = –0.8387 dan 0o < θ < 360o
(d) tan θ = –1.732 dan 0o < θ < 360o
Penyelesaian:
(a)

sin θ = 0.6025
Sudut asas ∠ = 37.05o ← (tekan SHIFT sin-1 0.6025 = 37.04975756)
Oleh itu θ = 180o – 37.05o = 142.95o ← (90o < θ < 180o)
(b)

kos θ = –0.6025
Sudut asas ∠ = 52.95o ← (tekan SHIFT kos-1 0.6025 = 52.9508)
Oleh itu θ = 180o + 52.95o = 232.95o ← (180o < θ < 270o)
(c)

sin θ = –0.8387 ← (sin θ adalah negatif dalam sukuan ke III dan ke IV)
Sudut asas ∠ = 57o ← (tekan SHIFT sin-1 0.8387 = 57.003)
θ1 = 180o + 57o = 237o ← (180o < θ < 270o)
θ2 = 360o – 57o = 303o ← (270o < θ < 360o)
Oleh itu θ = 237o dan 303o
(d)

tan θ = –1.732 ← (tan θ adalah negatif dalam sukuan ke II dan ke IV)
Sudut asas ∠ = 60o ← (tekan SHIFT tan-1 1.732 = 59.9993)
θ1 = 180o – 60o = 120o ← (90o < θ < 180o)
θ2 = 360o – 60o = 300o ← (270o < θ < 360o)
Oleh itu θ = 120o dan 300o