Soalan 1:
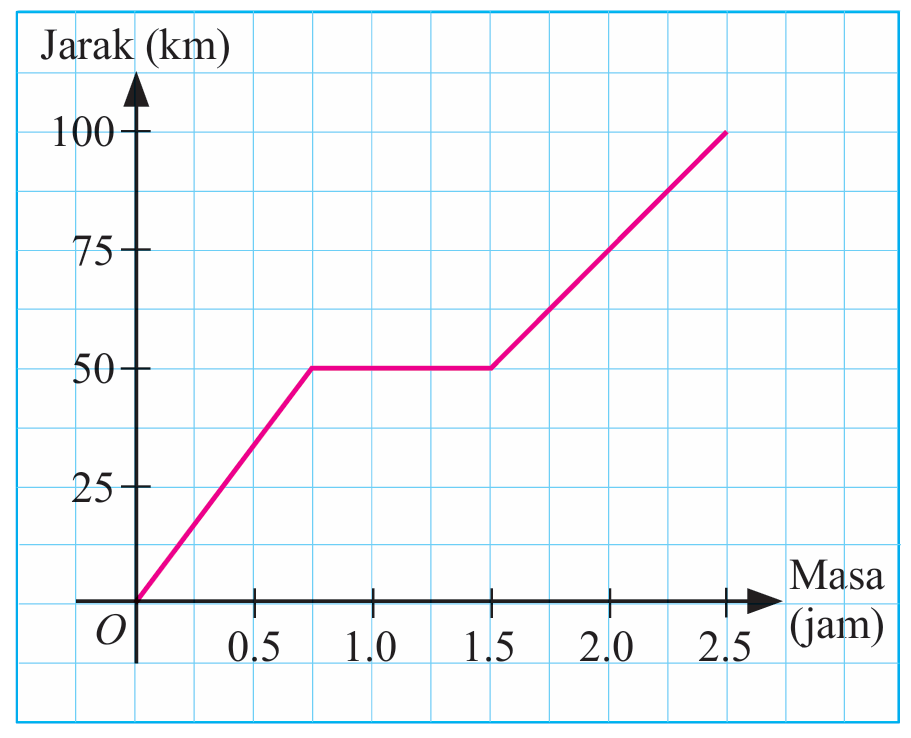
Graf jarak-masa di sebelah menunjukkan perjalanan Encik Rejab dari Kota Kinabalu ke Keningau bersama-sama ahli keluarganya untuk menyambut Pesta Kaamatan dengan menaiki kereta.
(a) Hitung laju kereta dalam km j–1 untuk sejam yang terakhir.
(b) Huraikan gerakan kereta Encik Rejab untuk tempoh 45 minit selepas bergerak sejauh 50 km yang pertama.
(c)(i) Hitung laju purata, dalam km j–1 bagi perjalanan dari Kota Kinabalu ke Keningau.
(ii) Seterusnya, huraikan gerakan kereta bagi keseluruhan perjalanan.
Penyelesaian:
(a)
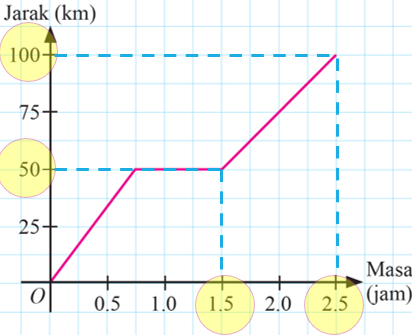
$$ \begin{aligned} & \text { Laju }=\frac{\text { Jarak }}{\text { Masa }} \\ & \begin{aligned} \text { Laju } & =\frac{(100-50) \mathrm{km}}{(2.5-1.5) j} \\ & =50 \mathrm{~km} \mathrm{j}^{-1} \end{aligned} \end{aligned} $$
(b) Kereta berada dalam keadaan pegun.
(c)(i)
$$ \begin{aligned} & \text { Laju purata }=\frac{\text { Jumlah jarak dilalui }}{\text { Jumlah masa diambil }} \\ & \begin{aligned} \text { Laju purata } & =\frac{100 \mathrm{~km}}{2.5 \mathrm{j}} \\ & =40 \mathrm{~km} \mathrm{j}^{-1} \end{aligned} \end{aligned} $$
(c)(ii)
Kereta bergerak sejauh 100 km dengan laju purata 40 km j–1 dalam tempoh 2.5 jam.

Graf jarak-masa di sebelah menunjukkan perjalanan Encik Rejab dari Kota Kinabalu ke Keningau bersama-sama ahli keluarganya untuk menyambut Pesta Kaamatan dengan menaiki kereta.
(a) Hitung laju kereta dalam km j–1 untuk sejam yang terakhir.
(b) Huraikan gerakan kereta Encik Rejab untuk tempoh 45 minit selepas bergerak sejauh 50 km yang pertama.
(c)(i) Hitung laju purata, dalam km j–1 bagi perjalanan dari Kota Kinabalu ke Keningau.
(ii) Seterusnya, huraikan gerakan kereta bagi keseluruhan perjalanan.
Penyelesaian:
(a)

$$ \begin{aligned} & \text { Laju }=\frac{\text { Jarak }}{\text { Masa }} \\ & \begin{aligned} \text { Laju } & =\frac{(100-50) \mathrm{km}}{(2.5-1.5) j} \\ & =50 \mathrm{~km} \mathrm{j}^{-1} \end{aligned} \end{aligned} $$
(b) Kereta berada dalam keadaan pegun.
(c)(i)
$$ \begin{aligned} & \text { Laju purata }=\frac{\text { Jumlah jarak dilalui }}{\text { Jumlah masa diambil }} \\ & \begin{aligned} \text { Laju purata } & =\frac{100 \mathrm{~km}}{2.5 \mathrm{j}} \\ & =40 \mathrm{~km} \mathrm{j}^{-1} \end{aligned} \end{aligned} $$
(c)(ii)
Kereta bergerak sejauh 100 km dengan laju purata 40 km j–1 dalam tempoh 2.5 jam.
Soalan 2:
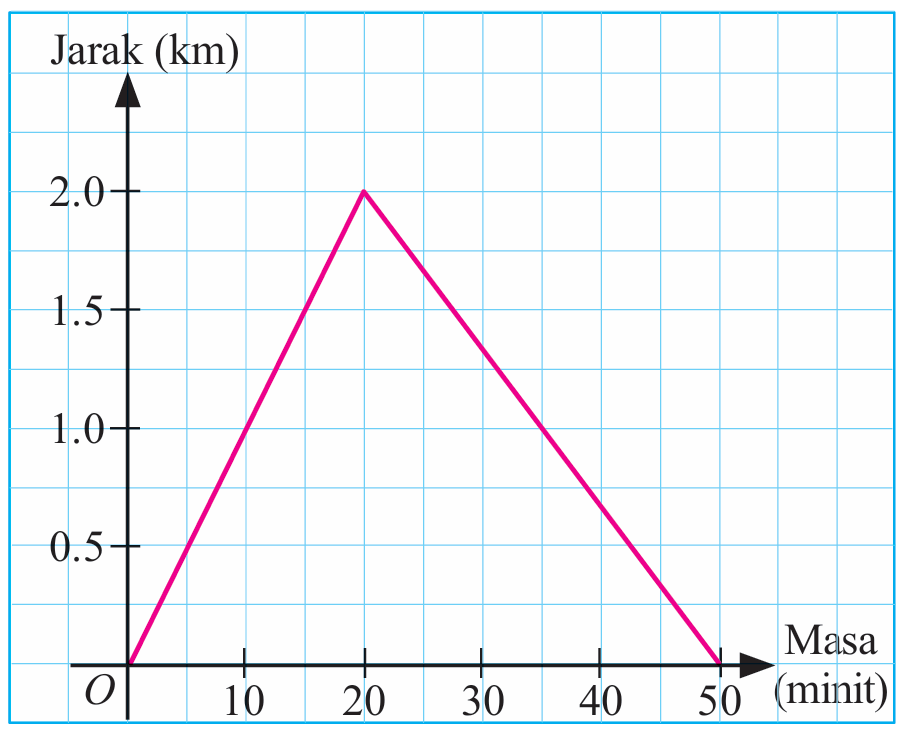
Encik Rashid bersenam setiap hari untuk menjaga kesihatan dirinya. Graf jarak-masa di sebelah menunjukkan jarak dan masa larian Encik Rashid dari rumahnya ke taman permainan dan balik ke rumahnya semula.
(a) Hitung beza laju larian Encik Rashid dari rumah ke taman permainan dan dari taman permainan ke rumahnya dalam km j–1.
(b) Hitung laju purata keseluruhan larian Encik Rashid dalam km j–1.
(c) Huraikan gerakan Encik Rashid untuk tempoh 50 minit.
Penyelesaian:
$$ \text { Laju }=\frac{\text { Jarak }}{\text { Masa }} $$
(a)
$$ \begin{aligned} \text { Laju dari rumah ke taman permainan } & =\frac{(2.0-0) \mathrm{km}}{\left(\frac{20-0}{60}\right) \mathrm{j}} \\ & =6 \mathrm{~km} \mathrm{j}^{-1} \end{aligned} $$
$$ \begin{aligned} \text { Laju dari taman permainan ke rumah } & =\frac{(0-2.0) \mathrm{km}}{\left(\frac{50-20}{60}\right) \mathrm{j}} \\ & =-4 \mathrm{~km} \mathrm{j}^{-1} \\ & =4 \mathrm{~km} \mathrm{j}^{-1} \end{aligned} $$
$$ \begin{aligned} \text { Beza laju } & =(6-4) \mathrm{km} \mathrm{j}^{-1} \\ & =2 \mathrm{~km} \mathrm{j}^{-1} \end{aligned} $$
(b)
$$ \begin{aligned} & \text { Laju purata }=\frac{\text { Jumlah jarak dilalui }}{\text { Jumlah masa diambil }} \\ & \begin{aligned} \text { Laju purata } & =\frac{(2.0+2.0) \mathrm{km}}{\left(\frac{50}{60}\right) \mathrm{j}} \\ & =4.8 \mathrm{~km} \mathrm{j}^{-1} \end{aligned} \end{aligned} $$
(c)
En. Rashid berlari sejauh 4.0 km “dengan laju purata 4.8 km j–1 dalam tempoh 50 minit.

Encik Rashid bersenam setiap hari untuk menjaga kesihatan dirinya. Graf jarak-masa di sebelah menunjukkan jarak dan masa larian Encik Rashid dari rumahnya ke taman permainan dan balik ke rumahnya semula.
(a) Hitung beza laju larian Encik Rashid dari rumah ke taman permainan dan dari taman permainan ke rumahnya dalam km j–1.
(b) Hitung laju purata keseluruhan larian Encik Rashid dalam km j–1.
(c) Huraikan gerakan Encik Rashid untuk tempoh 50 minit.
Penyelesaian:
$$ \text { Laju }=\frac{\text { Jarak }}{\text { Masa }} $$
(a)
$$ \begin{aligned} \text { Laju dari rumah ke taman permainan } & =\frac{(2.0-0) \mathrm{km}}{\left(\frac{20-0}{60}\right) \mathrm{j}} \\ & =6 \mathrm{~km} \mathrm{j}^{-1} \end{aligned} $$
$$ \begin{aligned} \text { Laju dari taman permainan ke rumah } & =\frac{(0-2.0) \mathrm{km}}{\left(\frac{50-20}{60}\right) \mathrm{j}} \\ & =-4 \mathrm{~km} \mathrm{j}^{-1} \\ & =4 \mathrm{~km} \mathrm{j}^{-1} \end{aligned} $$
$$ \begin{aligned} \text { Beza laju } & =(6-4) \mathrm{km} \mathrm{j}^{-1} \\ & =2 \mathrm{~km} \mathrm{j}^{-1} \end{aligned} $$
(b)
$$ \begin{aligned} & \text { Laju purata }=\frac{\text { Jumlah jarak dilalui }}{\text { Jumlah masa diambil }} \\ & \begin{aligned} \text { Laju purata } & =\frac{(2.0+2.0) \mathrm{km}}{\left(\frac{50}{60}\right) \mathrm{j}} \\ & =4.8 \mathrm{~km} \mathrm{j}^{-1} \end{aligned} \end{aligned} $$
(c)
En. Rashid berlari sejauh 4.0 km “dengan laju purata 4.8 km j–1 dalam tempoh 50 minit.
Soalan 3:
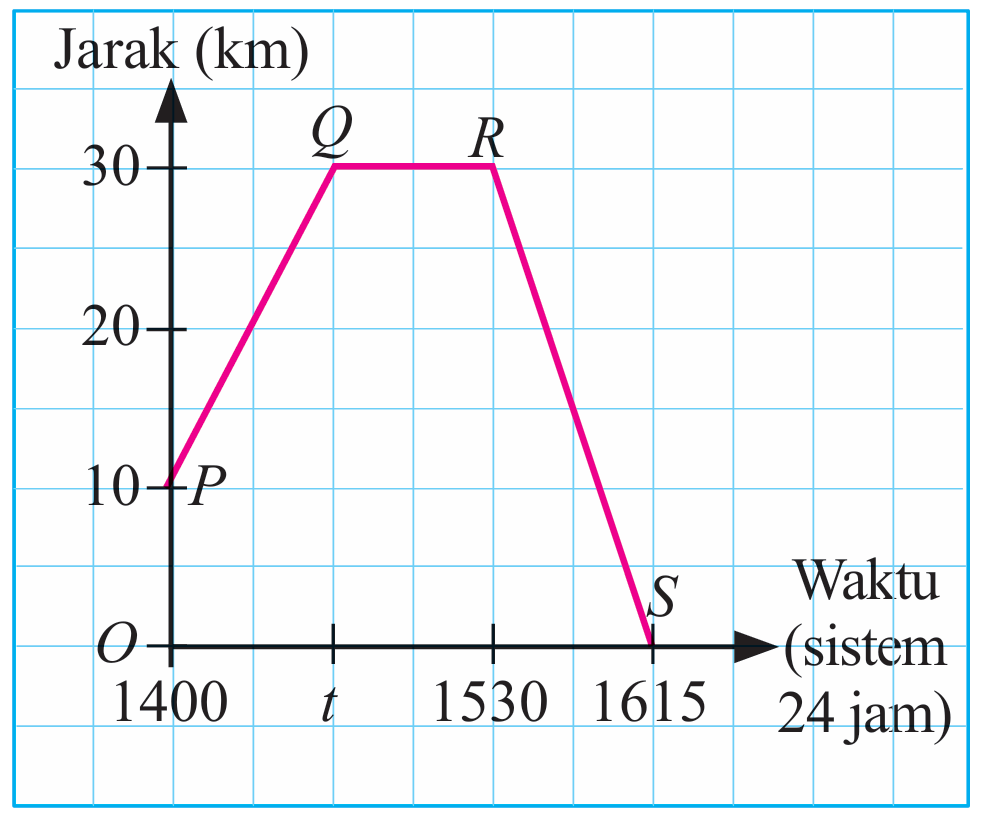
Graf jarak-masa di sebelah menunjukkan perjalanan Puan Rozita untuk tempoh 2¼ jam dengan memandu keretanya. PQ ialah perjalanan Puan Rozita dari tempat kerjanya ke sebuah pasar raya dan RS ialah perjalanan balik ke rumahnya.
(a) Hitung nilai t jika laju kereta semasa perjalanan dari tempat kerja ke pasar raya ialah 50 km j–1.
(b) Huraikan gerakan kereta yang mewakili
(i) garis lurus QR
(ii) garis lurus RS
Penyelesaian:
(a)
$$ \begin{aligned} \text { Masa } & =\frac{\text { jarak }}{\text { laju }} \\ & =\frac{(30-10) \mathrm{km}}{50 \mathrm{~km} \mathrm{j}^{-1}} \\ & =0.4 \mathrm{j} \\ & =24 \text { minit } \\ t & =1400+0024 \\ & =1424 \end{aligned} $$
(b)(i)
$$ \begin{aligned} 1530-1424 & =0106 \\ & =1 \text { jam } 6 \text { minit } \\ & =66 \text { minit } \end{aligned} $$
Kereta berada dalam keadaan pegun untuk tempoh 66 minit.
(b)(ii)
$$ \begin{aligned} \text { Laju } & =\frac{(0-30) \mathrm{km}}{\left(\frac{1615-1530}{60}\right) \mathrm{j}} \\ & =\frac{-30 \mathrm{~km}}{\frac{3}{4} \mathrm{j}} \\ & =-40 \mathrm{~km} j^{-1} \\ & =40 \mathrm{~km} \mathrm{j}^{-1} \end{aligned} $$
Kereta bergerak dengan laju 40 km j–1 sejauh 30 km dalam tempoh 45 minit.

Graf jarak-masa di sebelah menunjukkan perjalanan Puan Rozita untuk tempoh 2¼ jam dengan memandu keretanya. PQ ialah perjalanan Puan Rozita dari tempat kerjanya ke sebuah pasar raya dan RS ialah perjalanan balik ke rumahnya.
(a) Hitung nilai t jika laju kereta semasa perjalanan dari tempat kerja ke pasar raya ialah 50 km j–1.
(b) Huraikan gerakan kereta yang mewakili
(i) garis lurus QR
(ii) garis lurus RS
Penyelesaian:
(a)
$$ \begin{aligned} \text { Masa } & =\frac{\text { jarak }}{\text { laju }} \\ & =\frac{(30-10) \mathrm{km}}{50 \mathrm{~km} \mathrm{j}^{-1}} \\ & =0.4 \mathrm{j} \\ & =24 \text { minit } \\ t & =1400+0024 \\ & =1424 \end{aligned} $$
(b)(i)
$$ \begin{aligned} 1530-1424 & =0106 \\ & =1 \text { jam } 6 \text { minit } \\ & =66 \text { minit } \end{aligned} $$
Kereta berada dalam keadaan pegun untuk tempoh 66 minit.
(b)(ii)
$$ \begin{aligned} \text { Laju } & =\frac{(0-30) \mathrm{km}}{\left(\frac{1615-1530}{60}\right) \mathrm{j}} \\ & =\frac{-30 \mathrm{~km}}{\frac{3}{4} \mathrm{j}} \\ & =-40 \mathrm{~km} j^{-1} \\ & =40 \mathrm{~km} \mathrm{j}^{-1} \end{aligned} $$
Kereta bergerak dengan laju 40 km j–1 sejauh 30 km dalam tempoh 45 minit.
Soalan 4:
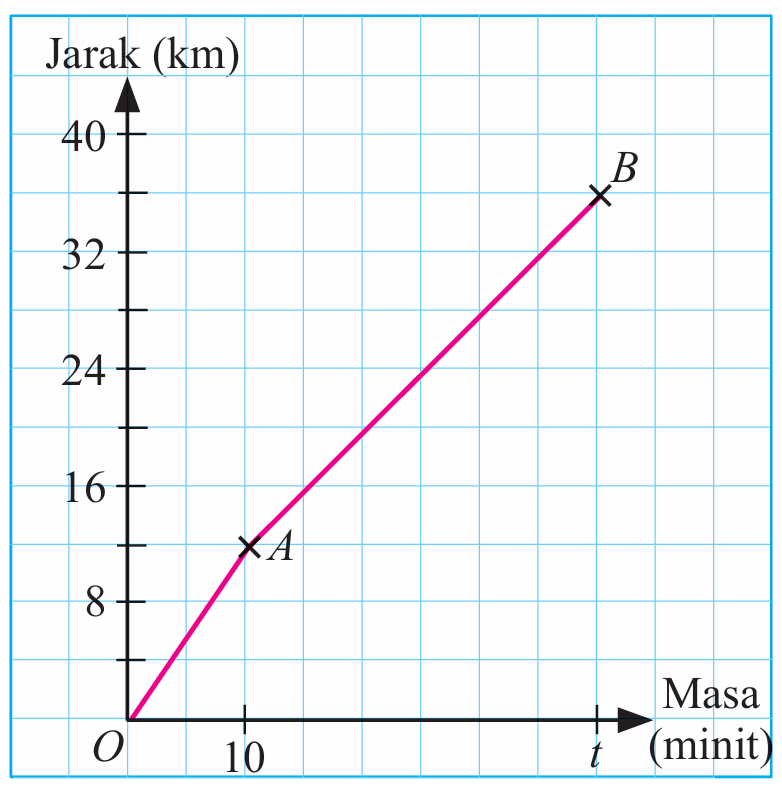
Encik Yusri bekerja di sebuah firma guaman. Setiap hari Encik Yusri akan menghantar anaknya ke sekolah dalam perjalanan ke tempat kerja dengan menaiki kereta. OA merupakan perjalanan dari rumah ke sekolah dan AB ialah perjalanan dari sekolah ke tempat kerja.
(a) Hitung nilai t, jika kadar perubahan jarak terhadap masa kereta dari sekolah ke tempat kerja ialah 48 km j–1.
(b) Huraikan gerakan kereta bagi keseluruhan perjalanan dari rumah ke tempat kerja.
Penyelesaian:
(a)
$$ \begin{aligned} &\text { Kadar perubahan jarak terhadap masa = laju }\\ &\begin{aligned} \text { Laju } & =\frac{\text { jarak }}{\text { Masa }} \\ 48 \mathrm{~km} \mathrm{j}^{-1} & =\frac{(36-12) \mathrm{km}}{\left(\frac{t-10}{60}\right) \mathrm{j}} \\ 48 \times \frac{t-10}{60} & =24 \\ \frac{t-10}{60} & =\frac{24}{48} \\ t-10 & =\frac{1}{2} \times 60 \\ t & =30+10 \\ t & =40 \text { minit } \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} & \text { Laju purata }=\frac{\text { Jumlah jarak dilalui }}{\text { Jumlah masa diambil }} \\ & \begin{aligned} \text { Laju purata } & =\frac{36 \mathrm{~km}}{\left(\frac{40}{60}\right) \mathrm{j}} \\ & =54 \mathrm{~km} \mathrm{j}^{-1} \end{aligned} \end{aligned} $$
Kereta bergerak dengan laju purata 54 km j-1 sejauh 36 km dalam tempoh 40 minit.

Encik Yusri bekerja di sebuah firma guaman. Setiap hari Encik Yusri akan menghantar anaknya ke sekolah dalam perjalanan ke tempat kerja dengan menaiki kereta. OA merupakan perjalanan dari rumah ke sekolah dan AB ialah perjalanan dari sekolah ke tempat kerja.
(a) Hitung nilai t, jika kadar perubahan jarak terhadap masa kereta dari sekolah ke tempat kerja ialah 48 km j–1.
(b) Huraikan gerakan kereta bagi keseluruhan perjalanan dari rumah ke tempat kerja.
Penyelesaian:
(a)
$$ \begin{aligned} &\text { Kadar perubahan jarak terhadap masa = laju }\\ &\begin{aligned} \text { Laju } & =\frac{\text { jarak }}{\text { Masa }} \\ 48 \mathrm{~km} \mathrm{j}^{-1} & =\frac{(36-12) \mathrm{km}}{\left(\frac{t-10}{60}\right) \mathrm{j}} \\ 48 \times \frac{t-10}{60} & =24 \\ \frac{t-10}{60} & =\frac{24}{48} \\ t-10 & =\frac{1}{2} \times 60 \\ t & =30+10 \\ t & =40 \text { minit } \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} & \text { Laju purata }=\frac{\text { Jumlah jarak dilalui }}{\text { Jumlah masa diambil }} \\ & \begin{aligned} \text { Laju purata } & =\frac{36 \mathrm{~km}}{\left(\frac{40}{60}\right) \mathrm{j}} \\ & =54 \mathrm{~km} \mathrm{j}^{-1} \end{aligned} \end{aligned} $$
Kereta bergerak dengan laju purata 54 km j-1 sejauh 36 km dalam tempoh 40 minit.