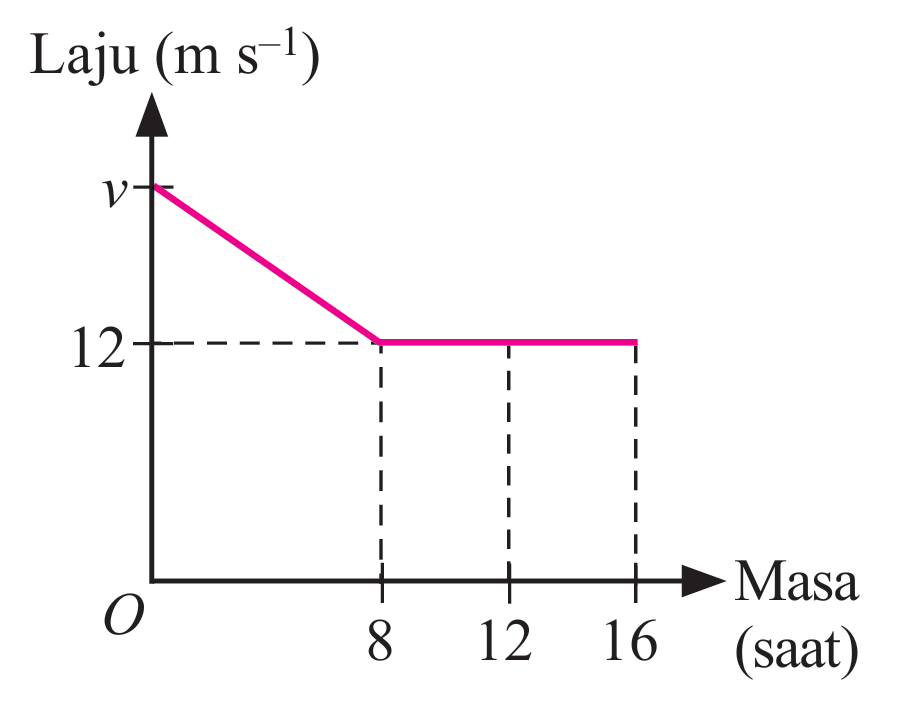
Graf laju-masa di sebelah menunjukkan gerakan kereta Dion Johan untuk tempoh 16 saat. Hitung,
(a) jarak dalam meter, yang dilalui semasa kereta bergerak dengan laju seragam.
(b) nilai v, jika laju purata kereta untuk 12 saat yang pertama ialah 14 m s–1.
Penyelesaian:
(a)
$$
\text { Jarak gerakan = Luas di bawah graf }
$$
$$
\begin{aligned}
&\text { Jarak dilalui semasa kereta bergerak dengan laju seragam }\\
&\begin{aligned}
& =(16-8) \times 12 \\
& =96 \mathrm{~m}
\end{aligned}
\end{aligned}
$$
(b)
$$
\text { Laju purata }=\frac{\text { Jumlah jarak }}{\text { Jumlah masa }}
$$
$$
\begin{aligned}
&\text { Laju purata untuk } 12 \mathrm{~s} \text { pertama }=14 \mathrm{~ms}^{-1}\\
&\begin{aligned}
\frac{\frac{1}{2} \times(12+v) \times 8+(12-8) \times 12}{12} & =14 \\
48+4 v+48 & =14 \times 12 \\
4 v+96 & =168 \\
4 v & =72 \\
v & =18 \mathrm{~ms}^{-1}
\end{aligned}
\end{aligned}
$$
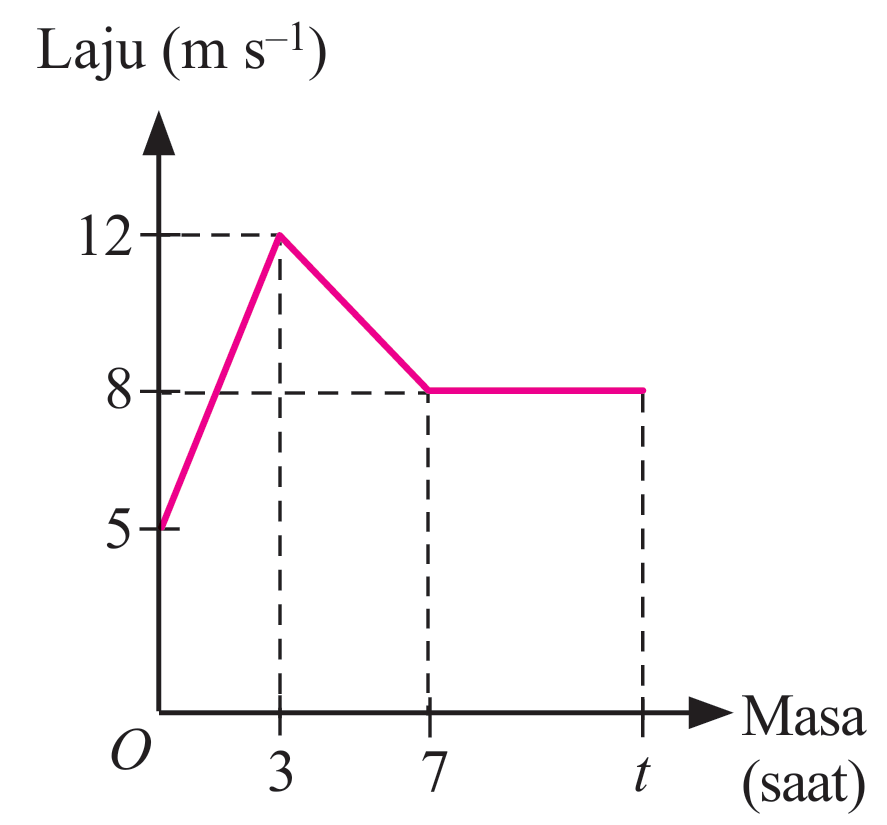
Graf laju-masa di sebelah mewakili gerakan motosikal yang dipandu oleh Abit Lusang untuk tempoh t saat.
Hitung,
(a) nyahpecutan gerakan dalam m s–2.
(b) jarak dalam meter semasa kadar perubahan laju terhadap masa adalah bernilai positif.
(c) nilai t, jika jumlah jarak yang dilalui untuk tempoh t saat ialah 121.5 m.
Penyelesaian:
(a)
$$
\begin{aligned}
\text { Kadar perubahan laju } & =\frac{(8-12) \mathrm{ms}^{-1}}{(7-3) \mathrm{s}} \\
& =-1 \mathrm{~ms}^{-2} \\
\text { Nyahpecutan } & =1 \mathrm{~ms}^{-2}
\end{aligned}
$$
(b)
$$
\begin{aligned}
&\text { Jarak semasa kadar perubahan laju terhadap masa adalah positif }\\
&\begin{aligned}
& =\frac{1}{2} \times(5+12) \times 3 \\
& =25.5 \mathrm{~m}
\end{aligned}
\end{aligned}
$$
(c)
$$
\begin{aligned}
\text { Jumlah jarak } & =121.5 \mathrm{~m} \\
25.5+\frac{1}{2} \times(12+8) \times(7-3)+(t-7) \times 8 & =121.5 \\
25.5+40+8 t-56 & =121.5 \\
8 t+9.5 & =121.5 \\
8 t & =112 \\
t & =14 \mathrm{~s}
\end{aligned}
$$
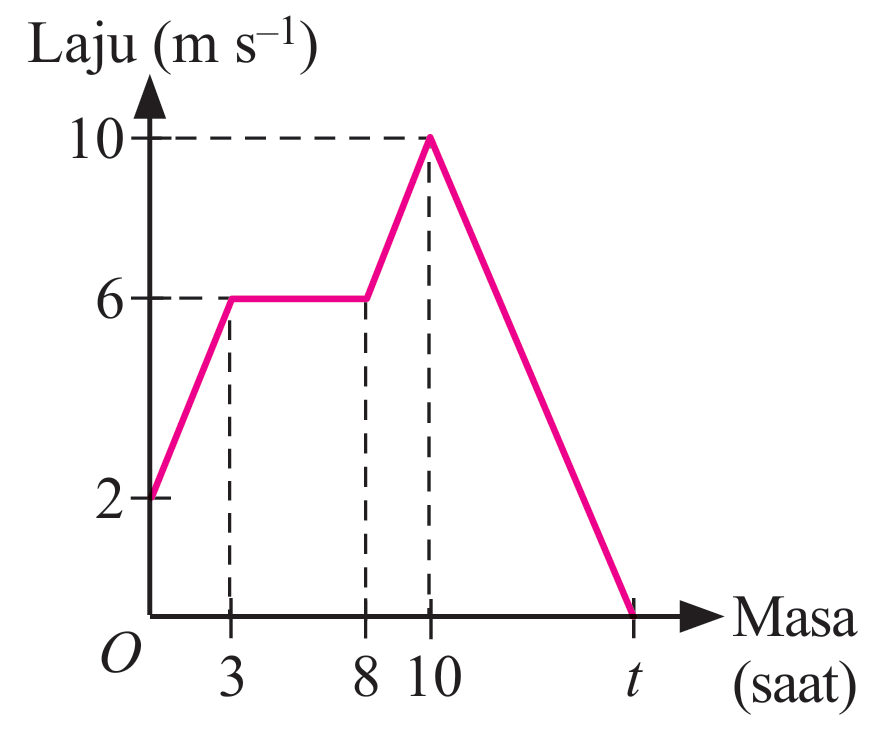
Graf laju-masa di sebelah menunjukkan gerakan sebuah kereta untuk tempoh t saat. Hitung,
(a) jumlah jarak, dalam meter, yang dilalui semasa kadar perubahan laju terhadap masa kereta tersebut bernilai positif.
(b) nilai t jika magnitud kadar perubahan laju terhadap masa dari saat ke-8 hingga saat ke-10 adalah sama dengan magnitud kadar perubahan laju terhadap masa selepas saat ke-10.
Penyelesaian:
(a)
Jumlah jarak yang dilalui semasa kadar perubahan laju terhadap masa bernilai positif
$$
\begin{aligned}
& =\frac{1}{2} \times(2+6) \times 3+\frac{1}{2} \times(6+10) \times(10-8) \\
& =12+16 \\
& =28 \mathrm{~m}
\end{aligned}
$$
(b)
Kadar perubahan laju terhadap masa dari saat ke-8 hingga saat ke-10 = Kadar perubahan laju terhadap masa selepas saat ke-10
$$
\begin{aligned}
\frac{(10-6) m s^{-1}}{(10-8) s} & =-\frac{(0-10) m s^{-1}}{(t-10) s} \\
2 & =-\frac{(-10)}{t-10} \\
2 \times(t-10) & =10 \\
2 t-20 & =10 \\
2 t & =30 \\
t & =15 s
\end{aligned}
$$