Soalan 1:

Graf jarak-masa di sebelah menunjukkan gerakan sebuah bas ekspres dalam masa 14 minit. Hitung,
(a) tempoh masa bas tersebut berada dalam keadaan pegun.
(b) kadar perubahan jarak terhadap masa untuk 4 minit yang terakhir dalam km j–1.
(c) laju purata bas untuk tempoh 14 minit dalam km j–1
Penyelesaian:
(a)
$$ \begin{aligned} &\text { Tempoh masa bas berada dalam keadaan pegun }\\ &\begin{aligned} & =(10-4) \text { minit } \\ & =6 \text { minit. } \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Kadar perubahan jarak terhadap masa untuk } 4 \text { minit terakhir }\\ &\begin{aligned} & =\frac{10-6}{\frac{(14-10)}{60}} \\ & =\frac{4}{4} \times 60 \\ & =60 \mathrm{kmj}^{-1} \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} \text { Laju purata bas untuk tempoh } 14 \text { minit } & =\frac{\text { Jumlah Jarak }}{\text { Jumlah masa }} \\ & =\frac{10}{14} \times 60 \\ & =42.86 \mathrm{kmj}^{-1} \end{aligned} $$

Graf jarak-masa di sebelah menunjukkan gerakan sebuah bas ekspres dalam masa 14 minit. Hitung,
(a) tempoh masa bas tersebut berada dalam keadaan pegun.
(b) kadar perubahan jarak terhadap masa untuk 4 minit yang terakhir dalam km j–1.
(c) laju purata bas untuk tempoh 14 minit dalam km j–1
Penyelesaian:
(a)
$$ \begin{aligned} &\text { Tempoh masa bas berada dalam keadaan pegun }\\ &\begin{aligned} & =(10-4) \text { minit } \\ & =6 \text { minit. } \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Kadar perubahan jarak terhadap masa untuk } 4 \text { minit terakhir }\\ &\begin{aligned} & =\frac{10-6}{\frac{(14-10)}{60}} \\ & =\frac{4}{4} \times 60 \\ & =60 \mathrm{kmj}^{-1} \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} \text { Laju purata bas untuk tempoh } 14 \text { minit } & =\frac{\text { Jumlah Jarak }}{\text { Jumlah masa }} \\ & =\frac{10}{14} \times 60 \\ & =42.86 \mathrm{kmj}^{-1} \end{aligned} $$
Soalan 2:
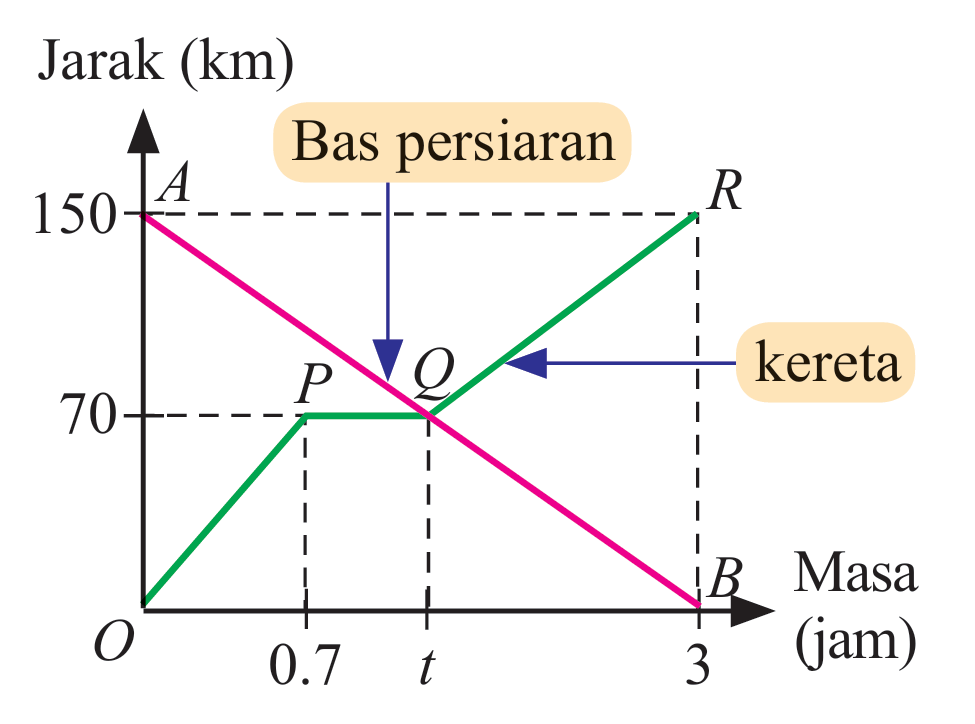
Sebuah kereta dan sebuah bas persiaran bergerak sejauh 150 km dalam masa 3 jam. Graf jarak-masa di sebelah menunjukkan gerakan kedua-dua kereta dan bas persiaran tersebut. Hitung,
(a) kadar perubahan jarak terhadap masa kereta, dalam km j–1 untuk 42 minit yang pertama.
(b) nilai t.
(c) kadar perubahan jarak terhadap masa kereta dalam km j–1 untuk gerakan 80 km terakhir.
Penyelesaian:
(a)
$$ \begin{aligned} &\text { Kadar perubahan jarak terhadap masa kereta untuk } 42 \text { minit yang pertama }\\ &\begin{aligned} & =\frac{70}{0.7} \\ & =100 \mathrm{kmj}^{-1} \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Kadar perubahan jarak terhadap masa bas persiaran pada } A B=Q B\\ &\begin{aligned} \frac{0-150}{3-0} & =\frac{0-70}{3-t} \\ \frac{-150}{3} & =\frac{-70}{3-t} \\ -450+150 t & =-210 \\ 150 t & =240 \\ t & =1.6 \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} &\text { kadar perubahan jarak terhadap masa kereta untuk gerakan }\\ &\begin{aligned} 80 \mathrm{~km} \text { terakhir } & =\frac{80}{(3-1.6)} \\ & =\frac{80}{1.4} \\ & =57.14 \mathrm{kmj}^{-1} \end{aligned} \end{aligned} $$

Sebuah kereta dan sebuah bas persiaran bergerak sejauh 150 km dalam masa 3 jam. Graf jarak-masa di sebelah menunjukkan gerakan kedua-dua kereta dan bas persiaran tersebut. Hitung,
(a) kadar perubahan jarak terhadap masa kereta, dalam km j–1 untuk 42 minit yang pertama.
(b) nilai t.
(c) kadar perubahan jarak terhadap masa kereta dalam km j–1 untuk gerakan 80 km terakhir.
Penyelesaian:
(a)
$$ \begin{aligned} &\text { Kadar perubahan jarak terhadap masa kereta untuk } 42 \text { minit yang pertama }\\ &\begin{aligned} & =\frac{70}{0.7} \\ & =100 \mathrm{kmj}^{-1} \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Kadar perubahan jarak terhadap masa bas persiaran pada } A B=Q B\\ &\begin{aligned} \frac{0-150}{3-0} & =\frac{0-70}{3-t} \\ \frac{-150}{3} & =\frac{-70}{3-t} \\ -450+150 t & =-210 \\ 150 t & =240 \\ t & =1.6 \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} &\text { kadar perubahan jarak terhadap masa kereta untuk gerakan }\\ &\begin{aligned} 80 \mathrm{~km} \text { terakhir } & =\frac{80}{(3-1.6)} \\ & =\frac{80}{1.4} \\ & =57.14 \mathrm{kmj}^{-1} \end{aligned} \end{aligned} $$
Soalan 3:
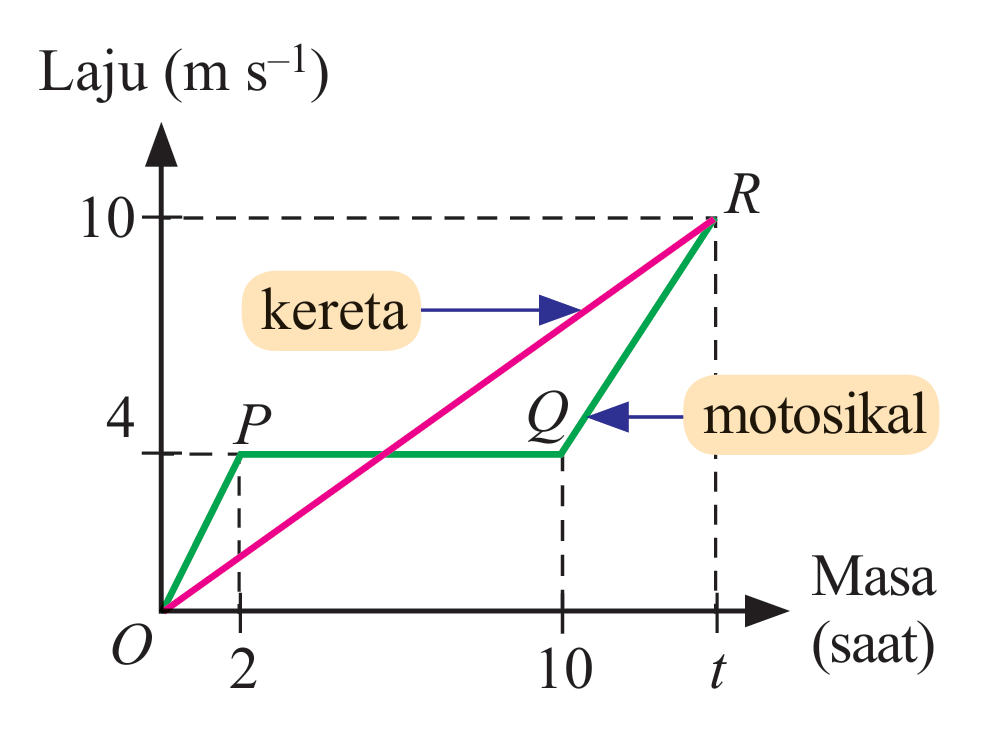
Graf laju-masa di sebelah menunjukkan gerakan sebuah kereta dan sebuah motosikal. Hitung,
(a) tempoh masa motosikal bergerak dengan laju seragam.
(b) nilai t, jika jarak yang dilalui oleh kereta dan motosikal adalah sama untuk tempoh t saat.
Penyelesaian:
(a)
$$ \begin{aligned} &\text { Tempoh masa motosikal bergerak dengan laju seragam }\\ &\begin{aligned} & =10-2 \\ & =8 \text { saat } \end{aligned} \end{aligned} $$
(b)
Jarak yang dilalui oleh kereta dan motosikal untuk tempoh t saat = Luas di bawah graf
$$ \begin{aligned} \frac{1}{2} \times t \times 10 & =\left(\frac{1}{2} \times 2 \times 4\right)+(8 \times 4)+\left(\frac{1}{2} \times(4+10) \times(t-10)\right) \\ 5 t & =4+32+[7(t-10)] \\ 5 t & =36+7 t-70 \\ 7 t-5 t & =70-36 \\ 2 t & =34 \\ t & =17 \end{aligned} $$

Graf laju-masa di sebelah menunjukkan gerakan sebuah kereta dan sebuah motosikal. Hitung,
(a) tempoh masa motosikal bergerak dengan laju seragam.
(b) nilai t, jika jarak yang dilalui oleh kereta dan motosikal adalah sama untuk tempoh t saat.
Penyelesaian:
(a)
$$ \begin{aligned} &\text { Tempoh masa motosikal bergerak dengan laju seragam }\\ &\begin{aligned} & =10-2 \\ & =8 \text { saat } \end{aligned} \end{aligned} $$
(b)
Jarak yang dilalui oleh kereta dan motosikal untuk tempoh t saat = Luas di bawah graf
$$ \begin{aligned} \frac{1}{2} \times t \times 10 & =\left(\frac{1}{2} \times 2 \times 4\right)+(8 \times 4)+\left(\frac{1}{2} \times(4+10) \times(t-10)\right) \\ 5 t & =4+32+[7(t-10)] \\ 5 t & =36+7 t-70 \\ 7 t-5 t & =70-36 \\ 2 t & =34 \\ t & =17 \end{aligned} $$