Soalan 1:
Tentukan sama ada ayat-ayat di bawah pernyataan atau bukan pernyataan. Berikan justifikasi anda.
(a) Marilah kita pergi bermain di padang.
(b) Malaysia terletak di benua Asia.
(c) Adakah 3 + 2 = 8?
(d) x + 3 > x – 8
(e) 3x + 5 = –7
Penyelesaian:
Pernyataan ialah suatu ayat yang dapat ditentukan nilai kebenarannya, iaitu sama ada benar atau palsu, tetapi bukan kedua-duanya.
(a) Marilah kita pergi bermain di padang.
Bukan Pernyataan kerana ayat itu tidak dapat ditentukan nilai kebenarannya.
(b) Malaysia terletak di benua Asia.
Pernyataan kerana ayat itu benar.
(c) Adakah 3 + 2 = 8?
Bukan Pernyataan kerana ayat itu tidak dapat ditentukan nilai kebenarannya. (Ayat tanya bukan satu pernyataan.)
(d) x + 3 > x – 8
$$ \begin{aligned} & \text { Check, } x+3>x-8 \\ & \text { Apabila } x=-2 \\ & \begin{aligned} (-2)+3 & >(-2)-8 \\ 1 & >-10 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Apabila } x=0\\ &\begin{gathered} (0)+3>(0)-8 \\ 3>-8 \end{gathered} \end{aligned} $$
$$ \begin{aligned} \text { Apabila } x & =10 \\ (10)+3 & >(10)-8 \\ 13 & >2 \end{aligned} $$
Pernyataan kerana ia benar.
(e) 3x + 5 = –7
Bukan Pernyataan kerana ayat itu tidak dapat ditentukan nilai kebenarannya.
Tentukan sama ada ayat-ayat di bawah pernyataan atau bukan pernyataan. Berikan justifikasi anda.
(a) Marilah kita pergi bermain di padang.
(b) Malaysia terletak di benua Asia.
(c) Adakah 3 + 2 = 8?
(d) x + 3 > x – 8
(e) 3x + 5 = –7
Penyelesaian:
Pernyataan ialah suatu ayat yang dapat ditentukan nilai kebenarannya, iaitu sama ada benar atau palsu, tetapi bukan kedua-duanya.
(a) Marilah kita pergi bermain di padang.
Bukan Pernyataan kerana ayat itu tidak dapat ditentukan nilai kebenarannya.
(b) Malaysia terletak di benua Asia.
Pernyataan kerana ayat itu benar.
(c) Adakah 3 + 2 = 8?
Bukan Pernyataan kerana ayat itu tidak dapat ditentukan nilai kebenarannya. (Ayat tanya bukan satu pernyataan.)
(d) x + 3 > x – 8
$$ \begin{aligned} & \text { Check, } x+3>x-8 \\ & \text { Apabila } x=-2 \\ & \begin{aligned} (-2)+3 & >(-2)-8 \\ 1 & >-10 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Apabila } x=0\\ &\begin{gathered} (0)+3>(0)-8 \\ 3>-8 \end{gathered} \end{aligned} $$
$$ \begin{aligned} \text { Apabila } x & =10 \\ (10)+3 & >(10)-8 \\ 13 & >2 \end{aligned} $$
Pernyataan kerana ia benar.
(e) 3x + 5 = –7
Bukan Pernyataan kerana ayat itu tidak dapat ditentukan nilai kebenarannya.
Soalan 2:
Bina satu pernyataan yang benar dengan menggunakan angka dan simbol yang diberikan.
(a) 23, +, 9, 40, >
(b) {3, 6, 9}, {3}, ⊂
(c) 5/6 , 1/4 , × , 10/3, =
(d) x2 + 3, ≤, (x + 3)2
(e) 3√, 9, 27, 12, =, +
Penyelesaian:
Bukan semua pernyataan matematik benar. Nilai kebenaran bagi semua pernyataan matematik boleh ditentukan.
(a)
$$ \begin{aligned} 23,+, 9,40 & > \\ 23+40 & >9 \\ \text { atau } 40 & >23+9 \end{aligned} $$
$$ \begin{aligned} &\text { Check, }\\ &\begin{aligned} 23+40 & >9 \\ 63 & >9 \\ \text { Atau, } 40 & >23+9 \\ 40 & >32 \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} & \{3,6,9\},\{3\}, \subset \\ & \{3\} \subset\{3,6,9\} \end{aligned} $$
(c)
$$ \begin{aligned} & \frac{5}{6}, \quad \frac{1}{4}, \quad \times, \quad \frac{10}{3},= \\ & \frac{1}{4} \times \frac{10}{3}=\frac{10}{12} \\ & \frac{1}{4} \times \frac{10}{3}=\frac{5}{6} \end{aligned} $$
(d)
$$ \begin{aligned} x^2+3, & \leq, \quad(x+3)^2 \\ x^2+3 & \leq(x+3)^2 \end{aligned} $$
$$ \begin{aligned} &\text { Check, }\\ &\begin{aligned} & x^2+3 \leq(x+3)^2 \\ & x^2+3 \leq(x+3)(x+3) \\ & x^2+3 \leq x^2+3 x+3 x+9 \\ & x^2+3 \leq x^2+6 x+9 \end{aligned} \end{aligned} $$
(e)
$$ \begin{aligned} & \sqrt[3]{,} 9,27,12=,+ \\ & \sqrt[3]{27}+9=12 \end{aligned} $$
$$ \begin{aligned} \text { Check, } \sqrt[3]{27}+9 & =12 \\ 3+9 & =12 \\ 12 & =12 \end{aligned} $$
Bina satu pernyataan yang benar dengan menggunakan angka dan simbol yang diberikan.
(a) 23, +, 9, 40, >
(b) {3, 6, 9}, {3}, ⊂
(c) 5/6 , 1/4 , × , 10/3, =
(d) x2 + 3, ≤, (x + 3)2
(e) 3√, 9, 27, 12, =, +
Penyelesaian:
Bukan semua pernyataan matematik benar. Nilai kebenaran bagi semua pernyataan matematik boleh ditentukan.
(a)
$$ \begin{aligned} 23,+, 9,40 & > \\ 23+40 & >9 \\ \text { atau } 40 & >23+9 \end{aligned} $$
$$ \begin{aligned} &\text { Check, }\\ &\begin{aligned} 23+40 & >9 \\ 63 & >9 \\ \text { Atau, } 40 & >23+9 \\ 40 & >32 \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} & \{3,6,9\},\{3\}, \subset \\ & \{3\} \subset\{3,6,9\} \end{aligned} $$
Ulangkaji: Set A ialah subset bagi set B jika semua unsur dalam set A terdapat dalam set B.
Hubungan ‘set A ialah subset bagi set B’ ditulis sebagai A ⊂ B.
(c)
$$ \begin{aligned} & \frac{5}{6}, \quad \frac{1}{4}, \quad \times, \quad \frac{10}{3},= \\ & \frac{1}{4} \times \frac{10}{3}=\frac{10}{12} \\ & \frac{1}{4} \times \frac{10}{3}=\frac{5}{6} \end{aligned} $$
(d)
$$ \begin{aligned} x^2+3, & \leq, \quad(x+3)^2 \\ x^2+3 & \leq(x+3)^2 \end{aligned} $$
$$ \begin{aligned} &\text { Check, }\\ &\begin{aligned} & x^2+3 \leq(x+3)^2 \\ & x^2+3 \leq(x+3)(x+3) \\ & x^2+3 \leq x^2+3 x+3 x+9 \\ & x^2+3 \leq x^2+6 x+9 \end{aligned} \end{aligned} $$
(e)
$$ \begin{aligned} & \sqrt[3]{,} 9,27,12=,+ \\ & \sqrt[3]{27}+9=12 \end{aligned} $$
$$ \begin{aligned} \text { Check, } \sqrt[3]{27}+9 & =12 \\ 3+9 & =12 \\ 12 & =12 \end{aligned} $$
Soalan 3:
Tentukan sama ada pernyataan di bawah benar atau palsu.
(a) Semua segi empat mempunyai sudut tepat.
(b) Sebilangan rombus mempunyai empat sisi yang sama.
(c) Semua segi tiga mempunyai sisi yang sama panjang.
(d) Sebilangan poligon mempunyai lima sisi.
(e) Semua bulatan boleh dibahagikan kepada lapan sektor yang sama saiz.
Penyelesaian:
Bukan semua pernyataan matematik benar. Nilai kebenaran bagi semua pernyataan matematik boleh ditentukan.
(a) Semua segi empat mempunyai sudut tepat.
Bukan semua segi empat mempunyai sudut tepat.
Contoh segi empat yang tidak mempunyai sudut tepat, trapezium dan lelayang,
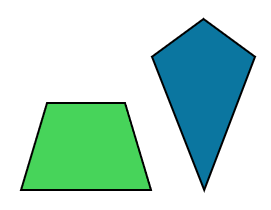Maka, pernyataan ini adalah palsu.
(b) Sebilangan rombus mempunyai empat sisi yang sama.
Ciri-ciri rombus adalah mempunyai sisi yang sama panjang.
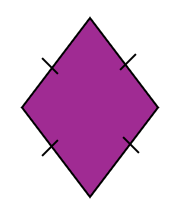
Maka, pernyataan ini adalah palsu.
(c) Semua segi tiga mempunyai sisi yang sama panjang.
Bukan semua segi tiga mempunyai sisi yang sama panjang.
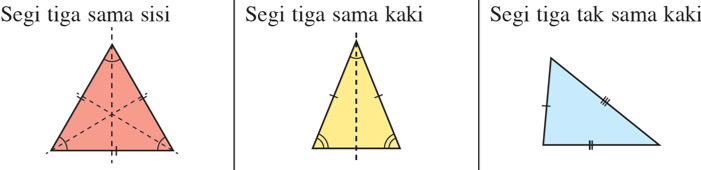
Maka, pernyataan ini adalah palsu.
(d) Sebilangan poligon mempunyai lima sisi.
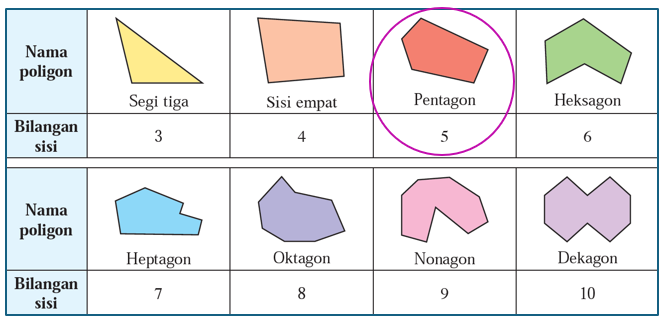
Ya, sebilangan poligon mempunyai lima sisi.
Maka, pernyataan ini adalah benar.
(e) Semua bulatan boleh dibahagikan kepada lapan sektor yang sama saiz.
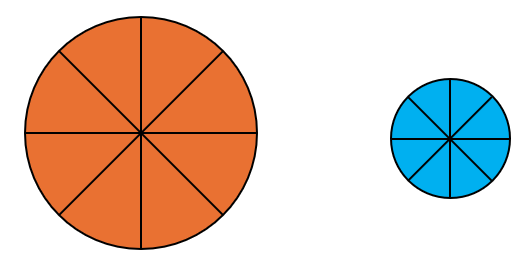
Ya, semua bulatan boleh dibahagikan kepada lapan sektor yang sama saiz.
Maka, pernyataan ini adalah benar.
Tentukan sama ada pernyataan di bawah benar atau palsu.
(a) Semua segi empat mempunyai sudut tepat.
(b) Sebilangan rombus mempunyai empat sisi yang sama.
(c) Semua segi tiga mempunyai sisi yang sama panjang.
(d) Sebilangan poligon mempunyai lima sisi.
(e) Semua bulatan boleh dibahagikan kepada lapan sektor yang sama saiz.
Penyelesaian:
Bukan semua pernyataan matematik benar. Nilai kebenaran bagi semua pernyataan matematik boleh ditentukan.
(a) Semua segi empat mempunyai sudut tepat.
Bukan semua segi empat mempunyai sudut tepat.
Contoh segi empat yang tidak mempunyai sudut tepat, trapezium dan lelayang,
Maka, pernyataan ini adalah palsu.(b) Sebilangan rombus mempunyai empat sisi yang sama.
Ciri-ciri rombus adalah mempunyai sisi yang sama panjang.
Maka, pernyataan ini adalah palsu.
(c) Semua segi tiga mempunyai sisi yang sama panjang.
Bukan semua segi tiga mempunyai sisi yang sama panjang.
Maka, pernyataan ini adalah palsu.
(d) Sebilangan poligon mempunyai lima sisi.
Ya, sebilangan poligon mempunyai lima sisi.
Maka, pernyataan ini adalah benar.
(e) Semua bulatan boleh dibahagikan kepada lapan sektor yang sama saiz.
Ya, semua bulatan boleh dibahagikan kepada lapan sektor yang sama saiz.
Maka, pernyataan ini adalah benar.