Soalan 11:
Selesaikan persamaan kuadratik berikut:
Penyelesaian:
Selesaikan persamaan kuadratik berikut:
Penyelesaian:
Soalan 12:
Selesaikan persamaan kuadratik berikut:
Penyelesaian:
Selesaikan persamaan kuadratik berikut:
Penyelesaian:
Soalan 13 (SPM 2016 – 4 markah):
Selesaikan persamaan kuadratik berikut:
Penyelesaian:
Selesaikan persamaan kuadratik berikut:
Penyelesaian:
Soalan 14 (SPM 2017 – 5 markah):
Penyelesaian dengan kaedah matriks tidak dibenarkan untuk menjawap soalan ini.
Rajah 3 menunjukkan sebuah basikal dan sebuah basikal roda tiga.
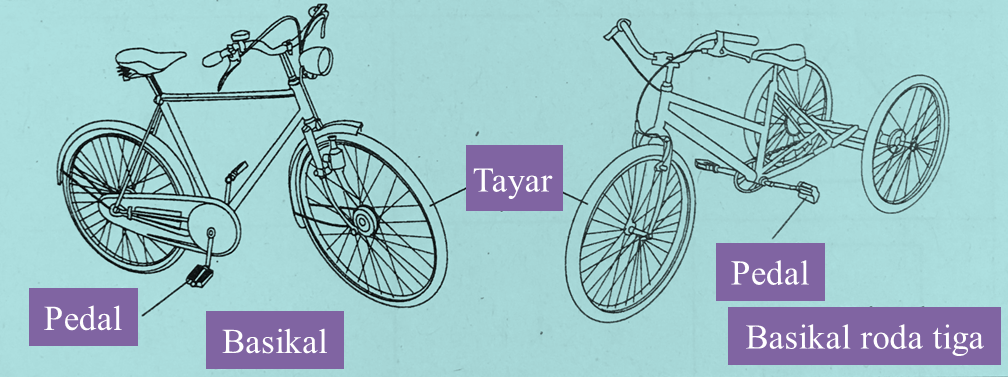
Hitung bilangan basikal dan bilangan basikal roda tiga jika terdapat 64 pedal dan 74 tayar.
Penyelesaian:
Katakan basikal = x dan basikal roda tiga = y
Jadi,
2x + 2y = 64 …………. (1)
2x + 3y = 74 …………. (2)
(2) – (1)
3y – 2y = 74 – 64
y = 10
Apabila y = 10
Dari (2)
2x + 3(10) = 74
2x = 74 – 30
2x = 44
x = 22
Maka, bilangan basikal ialah 22 dan bilangan basikal roda tiga ialah 10.
Penyelesaian dengan kaedah matriks tidak dibenarkan untuk menjawap soalan ini.
Rajah 3 menunjukkan sebuah basikal dan sebuah basikal roda tiga.

Hitung bilangan basikal dan bilangan basikal roda tiga jika terdapat 64 pedal dan 74 tayar.
Penyelesaian:
Katakan basikal = x dan basikal roda tiga = y
Jadi,
2x + 2y = 64 …………. (1)
2x + 3y = 74 …………. (2)
(2) – (1)
3y – 2y = 74 – 64
y = 10
Apabila y = 10
Dari (2)
2x + 3(10) = 74
2x = 74 – 30
2x = 44
x = 22
Maka, bilangan basikal ialah 22 dan bilangan basikal roda tiga ialah 10.
Soalan 15 (SPM 2018 – 4 markah):
Rajah 3 menunjukkan sebuah laluan taman berbentuk segi empat tepat. Terdapat 8 keping batu pemijak berbentuk bulat yang sama saiz dibina di laluan itu.

Diberi luas laluan itu ialah 32 m2, cari diameter, dalam m, sekeping batu pemijak itu.
Penyelesaian:
Rajah 3 menunjukkan sebuah laluan taman berbentuk segi empat tepat. Terdapat 8 keping batu pemijak berbentuk bulat yang sama saiz dibina di laluan itu.

Diberi luas laluan itu ialah 32 m2, cari diameter, dalam m, sekeping batu pemijak itu.
Penyelesaian:
Soalan 16 (SPM 2019):
Radziah membeli (2x – 17) buah kamus dengan harga RM12x setiap satu. Dia membayar RM4 104 untuk kesemua kamus itu.
Hitung bilangan kamus yang dia beli. [4 markah]
Penyelesaian:
Bilangan kamus dibeli = 2x – 17
Jumlah bayaran dibuat = 4104
12x(2x – 17) = 4104
x(2x – 17) = 342
2x2 – 17x – 342 = 0
(2x + 19)(x – 18) = 0
Radziah membeli (2x – 17) buah kamus dengan harga RM12x setiap satu. Dia membayar RM4 104 untuk kesemua kamus itu.
Hitung bilangan kamus yang dia beli. [4 markah]
Penyelesaian:
Bilangan kamus dibeli = 2x – 17
Jumlah bayaran dibuat = 4104
12x(2x – 17) = 4104
x(2x – 17) = 342
2x2 – 17x – 342 = 0
(2x + 19)(x – 18) = 0
Soalan 17 (SPM 2019):
Penyelesaian menggunakan kaedah matriks tidak dibenarkan untuk soalan ini.
Zul dan dua rakannya pergi ke sebuah restoran untuk sarapan pagi. Zul membayar harga RM 11
untuk semangkuk mee dan segelas jus oren. Roy membayar harga 3 mangkuk mee dan Vasu membayar 2 gelas jus oren. Pembezaan harga antara 3 mangkuk mee dan 2 gelas jus oren ialah RM7. Harga semangkuk mee adalah lebih tinggi daripada harga segelas jus oren.
Hitung harga, dalam RM, semangkuk mee dan segelas jus oren. [6 markah]
Penyelesaian:
Bayaran Zul = 11
Bayaran Zul – Bayaran Vasu = 7
x = harga semangkuk mee
y = harga segelas jus oren
x + y = 11 ………. (1)
3x – 2y = 7 ………. (2)
(1) × 2 : 2x + 2y = 22
(2) + (3) : 5x = 29
x = 5.80
Dari (1) : 5.80 + y = 11
y = 5.20
Maka, harga semangkuk mee ialah RM 5.80, manakala harga segelas jus oren ialah RM 5.20.
Penyelesaian menggunakan kaedah matriks tidak dibenarkan untuk soalan ini.
Zul dan dua rakannya pergi ke sebuah restoran untuk sarapan pagi. Zul membayar harga RM 11
untuk semangkuk mee dan segelas jus oren. Roy membayar harga 3 mangkuk mee dan Vasu membayar 2 gelas jus oren. Pembezaan harga antara 3 mangkuk mee dan 2 gelas jus oren ialah RM7. Harga semangkuk mee adalah lebih tinggi daripada harga segelas jus oren.
Hitung harga, dalam RM, semangkuk mee dan segelas jus oren. [6 markah]
Penyelesaian:
Bayaran Zul = 11
Bayaran Zul – Bayaran Vasu = 7
x = harga semangkuk mee
y = harga segelas jus oren
x + y = 11 ………. (1)
3x – 2y = 7 ………. (2)
(1) × 2 : 2x + 2y = 22
(2) + (3) : 5x = 29
x = 5.80
Dari (1) : 5.80 + y = 11
y = 5.20
Maka, harga semangkuk mee ialah RM 5.80, manakala harga segelas jus oren ialah RM 5.20.
Soalan 18 (SPM 2018 – 4 markah):
Penyelesaian menggunakan kaedah matriks tidak dibenarkan untuk soalan ini.
Rajah 5 menunjukkan kolam ikan berbentuk segi empat tepat dengan perimeter 62 m.
 Diberi bahawa panjang kolam adalah 3 kali lebar kolam itu.
Diberi bahawa panjang kolam adalah 3 kali lebar kolam itu.
Hitung panjang, dalam m, kolam ikan itu.
Penyelesaian:
Diberi y + 4 = 3x
y = 3x – 4 …………. (1)
Perimeter = 62
2x + 2(y + 4) = 62
2x + 2y + 8 = 62
2x + 2y = 54
(÷2) x + y = 27 …………. (2)
Gantikan (1) ke dalam (2):
x + 3x – 4 = 27
4x – 4 = 27
4x = 27 + 4
4x = 31
x = 7.75
Dari (1): y = 3x – 4
Apabila x = 7.75
y = 3(7.75) – 4
y = 19.25
Panjang kolam ikan
= y + 4
= 19.25 + 4
= 23.25 m
Penyelesaian menggunakan kaedah matriks tidak dibenarkan untuk soalan ini.
Rajah 5 menunjukkan kolam ikan berbentuk segi empat tepat dengan perimeter 62 m.
 Diberi bahawa panjang kolam adalah 3 kali lebar kolam itu.
Diberi bahawa panjang kolam adalah 3 kali lebar kolam itu.Hitung panjang, dalam m, kolam ikan itu.
Penyelesaian:
Diberi y + 4 = 3x
y = 3x – 4 …………. (1)
Perimeter = 62
2x + 2(y + 4) = 62
2x + 2y + 8 = 62
2x + 2y = 54
(÷2) x + y = 27 …………. (2)
Gantikan (1) ke dalam (2):
x + 3x – 4 = 27
4x – 4 = 27
4x = 27 + 4
4x = 31
x = 7.75
Dari (1): y = 3x – 4
Apabila x = 7.75
y = 3(7.75) – 4
y = 19.25
Panjang kolam ikan
= y + 4
= 19.25 + 4
= 23.25 m
Soalan 19 (SPM 2016 – 4 markah):
Hitung nilai x dan nilai y yang memuaskan persamaan linear serentak berikut:
2x + y = 8
–x + 4y = 5
Penyelesaian:
Hitung nilai x dan nilai y yang memuaskan persamaan linear serentak berikut:
2x + y = 8
–x + 4y = 5
Penyelesaian:
Soalan 20 (SPM 2017 – 4 markah):
Sebuah akuarium mempunyai panjang (x + 7) cm, lebar x cm dan tinggi 60 cm.
Jumlah isi padu akuarium itu ialah 48000 cm3. Akuarium itu akan diisi penuh dengan air.
Hitung nilai x.
Penyelesaian:
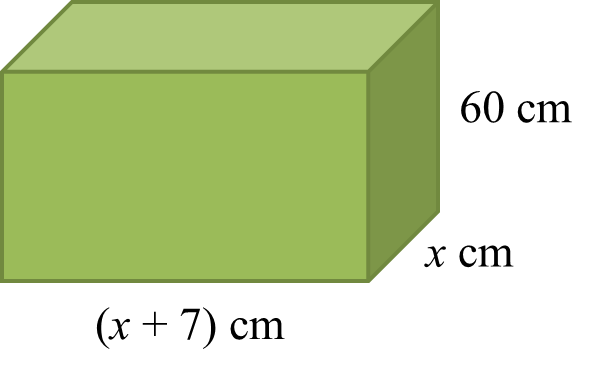
Sebuah akuarium mempunyai panjang (x + 7) cm, lebar x cm dan tinggi 60 cm.
Jumlah isi padu akuarium itu ialah 48000 cm3. Akuarium itu akan diisi penuh dengan air.
Hitung nilai x.
Penyelesaian:

perfect learning…ty