Soalan 1:
$$ \text { Nyatakan bilangan baris dan lajur bagi matriks }\left[\begin{array}{cc} 9 & -2 \\ 1 & 6 \\ 5 & 7 \end{array}\right] \text {. } $$
Penyelesaian:
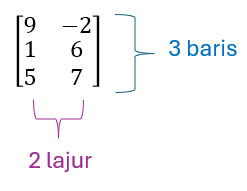
$$ \text { Nyatakan bilangan baris dan lajur bagi matriks }\left[\begin{array}{cc} 9 & -2 \\ 1 & 6 \\ 5 & 7 \end{array}\right] \text {. } $$
Penyelesaian:

Soalan 2:
$$ \text { Diberi } A=\left[\begin{array}{cc} 3 & 2 \\ 0 & -1 \\ 1 & 3 \end{array}\right], B=\left[\begin{array}{l} 1 \\ 4 \end{array}\right] \text { dan } A B=C \text {. } $$
$$ \text { Tentukan peringkat matriks } C \text {. } $$
Penyelesaian:
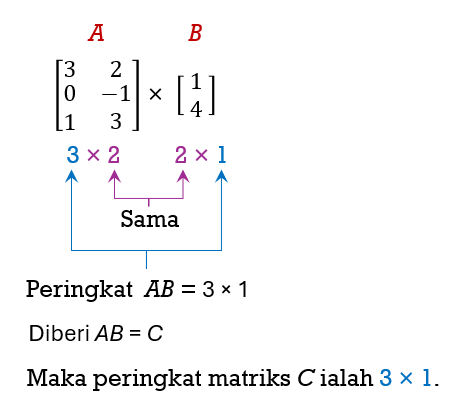
$$ \text { Diberi } A=\left[\begin{array}{cc} 3 & 2 \\ 0 & -1 \\ 1 & 3 \end{array}\right], B=\left[\begin{array}{l} 1 \\ 4 \end{array}\right] \text { dan } A B=C \text {. } $$
$$ \text { Tentukan peringkat matriks } C \text {. } $$
Penyelesaian:

Soalan 3:
$$ \text { Diberi matriks } D=\left[\begin{array}{cc} 4 & p \\ -2 & 3 \end{array}\right] \text {. } $$
$$ \text { Hitung nilai } p \text { jika penentu matriks } D \text { ialah } 0 \text {. } $$
Penyelesaian:
$$ \begin{aligned} &\text { Diberi }|D|=0\\ &\begin{aligned} 4(3)-p(-2) & =0 \\ 12+2 p & =0 \\ 2 p & =-12 \\ p & =-6 \end{aligned} \end{aligned} $$
$$ \text { Diberi matriks } D=\left[\begin{array}{cc} 4 & p \\ -2 & 3 \end{array}\right] \text {. } $$
$$ \text { Hitung nilai } p \text { jika penentu matriks } D \text { ialah } 0 \text {. } $$
Penyelesaian:
$$ \begin{aligned} &\text { Diberi }|D|=0\\ &\begin{aligned} 4(3)-p(-2) & =0 \\ 12+2 p & =0 \\ 2 p & =-12 \\ p & =-6 \end{aligned} \end{aligned} $$
Soalan 4:
$$ \text { Diberi matriks } E=\left[\begin{array}{cc} -1 & 2 \\ 5 & 4 \end{array}\right], $$
$$ \text { tunjukkan } E+E+E=3 E \text {. } $$
Penyelesaian:
$$ \begin{aligned} E+E+E & =\left[\begin{array}{cc} -1 & 2 \\ 5 & 4 \end{array}\right]+\left[\begin{array}{cc} -1 & 2 \\ 5 & 4 \end{array}\right]+\left[\begin{array}{cc} -1 & 2 \\ 5 & 4 \end{array}\right] \\ & =\left[\begin{array}{cc} -1+(-1)+(-1) & 2+2+2 \\ 5+5+5 & 4+4+4 \end{array}\right] \\ & =\left[\begin{array}{cc} -3 & 6 \\ 15 & 12 \end{array}\right] \end{aligned} $$
$$ \begin{aligned} &\begin{aligned} 3 E & =3\left[\begin{array}{cc} -1 & 2 \\ 5 & 4 \end{array}\right] \\ & =\left[\begin{array}{cc} 3(-1) & 3(2) \\ 3(5) & 3(4) \end{array}\right] \\ & =\left[\begin{array}{cc} -3 & 6 \\ 15 & 12 \end{array}\right] \end{aligned}\\ &\text { Maka, } E+E+E=3 E \quad \text { (Tertunjuk) } \end{aligned} $$
$$ \text { Diberi matriks } E=\left[\begin{array}{cc} -1 & 2 \\ 5 & 4 \end{array}\right], $$
$$ \text { tunjukkan } E+E+E=3 E \text {. } $$
Penyelesaian:
$$ \begin{aligned} E+E+E & =\left[\begin{array}{cc} -1 & 2 \\ 5 & 4 \end{array}\right]+\left[\begin{array}{cc} -1 & 2 \\ 5 & 4 \end{array}\right]+\left[\begin{array}{cc} -1 & 2 \\ 5 & 4 \end{array}\right] \\ & =\left[\begin{array}{cc} -1+(-1)+(-1) & 2+2+2 \\ 5+5+5 & 4+4+4 \end{array}\right] \\ & =\left[\begin{array}{cc} -3 & 6 \\ 15 & 12 \end{array}\right] \end{aligned} $$
$$ \begin{aligned} &\begin{aligned} 3 E & =3\left[\begin{array}{cc} -1 & 2 \\ 5 & 4 \end{array}\right] \\ & =\left[\begin{array}{cc} 3(-1) & 3(2) \\ 3(5) & 3(4) \end{array}\right] \\ & =\left[\begin{array}{cc} -3 & 6 \\ 15 & 12 \end{array}\right] \end{aligned}\\ &\text { Maka, } E+E+E=3 E \quad \text { (Tertunjuk) } \end{aligned} $$
Soalan 5:
Tuliskan persamaan linear serentak berikut dalam bentuk matriks.

Penyelesaian:
$$ \begin{aligned} m-3 & =4 n \\ m-4 n & =3 \end{aligned} $$
$$ \begin{array}{r} 3 m+2 n-2=0 \\ 3 m+2 n=2 \end{array} $$
$$ \left[\begin{array}{cc} 1 & -4 \\ 3 & 2 \end{array}\right]\left[\begin{array}{c} m \\ n \end{array}\right]=\left[\begin{array}{l} 3 \\ 2 \end{array}\right] $$
Tuliskan persamaan linear serentak berikut dalam bentuk matriks.

Penyelesaian:
$$ \begin{aligned} m-3 & =4 n \\ m-4 n & =3 \end{aligned} $$
$$ \begin{array}{r} 3 m+2 n-2=0 \\ 3 m+2 n=2 \end{array} $$
$$ \left[\begin{array}{cc} 1 & -4 \\ 3 & 2 \end{array}\right]\left[\begin{array}{c} m \\ n \end{array}\right]=\left[\begin{array}{l} 3 \\ 2 \end{array}\right] $$