Soalan 1:
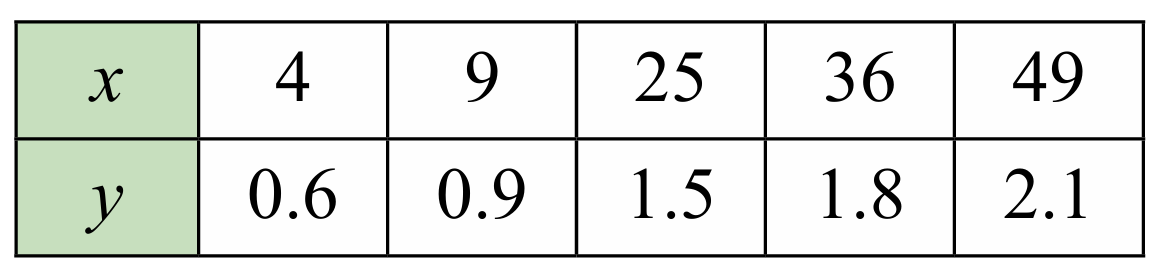
Jadual berikut menunjukkan nilai-nilai bagi dua pemboleh ubah, x dan y.
(a) Tentukan sama ada y berubah secara langsung dengan x atau x3. Kemudian, tuliskan hubungan tersebut dalam bentuk ubahan.

(b) Tentukan sama ada y berubah secara langsung dengan x atau √x. Kemudian, tuliskan hubungan tersebut dalam bentuk ubahan.
Penyelesaian:
(a)
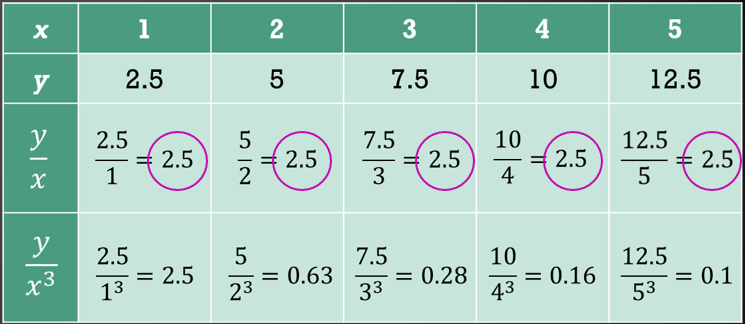
$$ y \text { berubah secara langsung dengan } x \text { kerana nilai } \frac{y}{x} \text { ialah pemalar. } $$
$$ \text { Maka y } \alpha x \text {. } $$
$$ y \text { tidak berubah secara langsung dengan } x^3 \text { kerana nilai } \frac{y}{x^3} \text { bukan pemalar. } $$
(b)
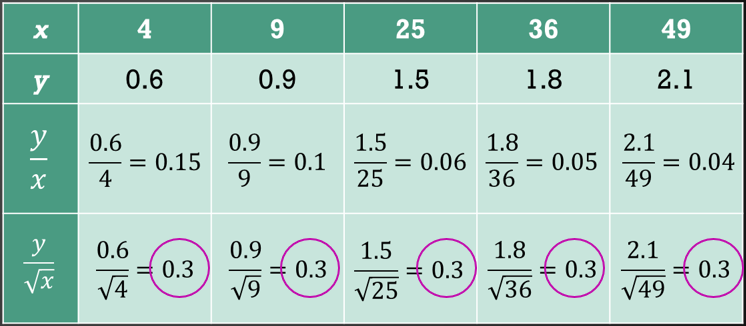
$$ y \text { tidak berubah secara langsung dengan } x \text { kerana nilai } \frac{y}{x} \text { bukan pemalar. } $$
$$ y \text { berubah secara langsung dengan } \sqrt{x} \text { kerana nilai } \frac{y}{\sqrt{x}} \text { ialah pemalar. } $$
$$ \text { Maka } y \alpha \sqrt{x} \text {. } $$
Jadual berikut menunjukkan nilai-nilai bagi dua pemboleh ubah, x dan y.
(a) Tentukan sama ada y berubah secara langsung dengan x atau x3. Kemudian, tuliskan hubungan tersebut dalam bentuk ubahan.

(b) Tentukan sama ada y berubah secara langsung dengan x atau √x. Kemudian, tuliskan hubungan tersebut dalam bentuk ubahan.

Penyelesaian:
(a)

$$ y \text { berubah secara langsung dengan } x \text { kerana nilai } \frac{y}{x} \text { ialah pemalar. } $$
$$ \text { Maka y } \alpha x \text {. } $$
$$ y \text { tidak berubah secara langsung dengan } x^3 \text { kerana nilai } \frac{y}{x^3} \text { bukan pemalar. } $$
(b)

$$ y \text { tidak berubah secara langsung dengan } x \text { kerana nilai } \frac{y}{x} \text { bukan pemalar. } $$
$$ y \text { berubah secara langsung dengan } \sqrt{x} \text { kerana nilai } \frac{y}{\sqrt{x}} \text { ialah pemalar. } $$
$$ \text { Maka } y \alpha \sqrt{x} \text {. } $$
Soalan 2:
Tentukan sama ada y berubah secara langsung dengan x atau √x. Kemudian, tuliskan hubungan tersebut dalam bentuk ubahan.
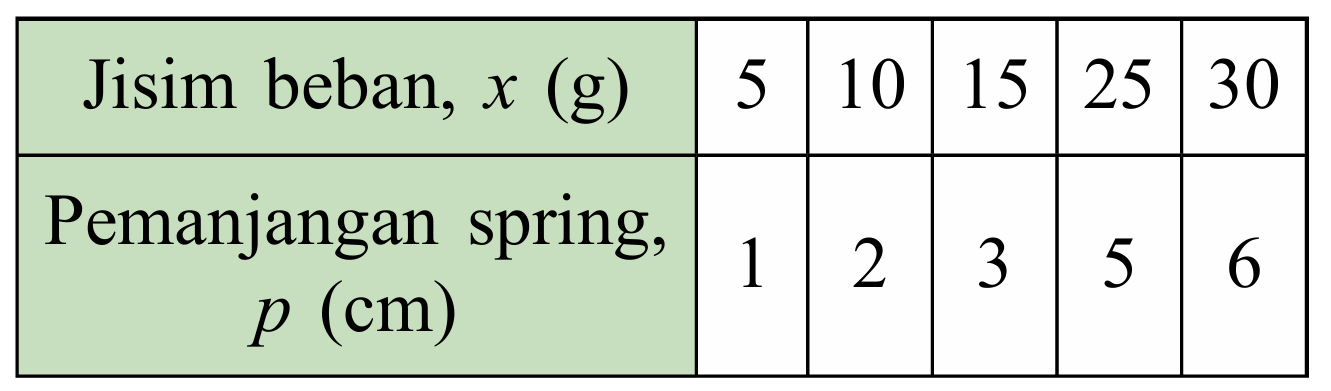
Penyelesaian:
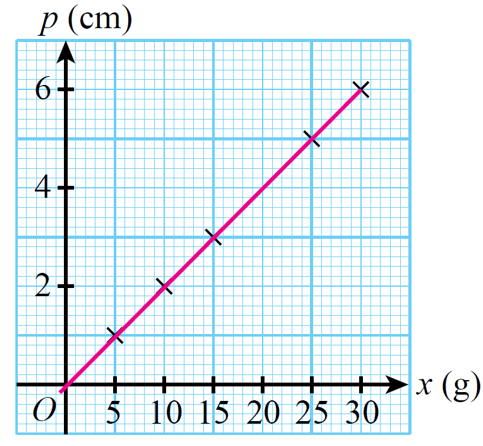
Tentukan sama ada y berubah secara langsung dengan x atau √x. Kemudian, tuliskan hubungan tersebut dalam bentuk ubahan.
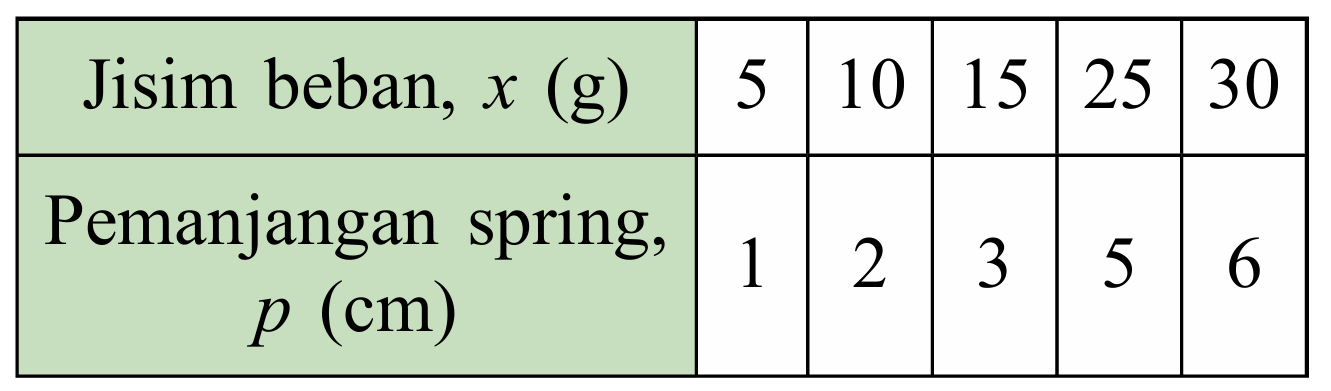
Penyelesaian:

Paksi-x: 1 cm : 5g
Paksi-y: 2 cm : 2 cm
Graf p melawan x menunjukkan satu garis lurus melalui asalan.
Maka, p berubah secara langsung dengan x.
Soalan 3:
Diberi p = 32 apabila q = 4. Ungkapkan p dalam sebutan q jika
(a) p berubah secara langsung dengan q3,
(b) p berubah secara langsung dengan punca kuasa dua q.
Penyelesaian:
$$ \text { Diberi } p=32, q=4 $$
(a)
$$ \begin{aligned} &\begin{aligned} & p \alpha q^3 \\ & p=k q^3 \\ & 32=k(4)^3 \\ & k=\frac{32}{4^3} \\ & k=0.5 \end{aligned}\\ &\text { Maka } p=0.5 q^3 \end{aligned} $$
(b)
$$ \begin{aligned} &\begin{aligned} & p \alpha \sqrt{q} \\ & p=k \sqrt{q} \\ & 32=k \sqrt{4} \\ & k=\frac{32}{\sqrt{4}} \\ & =16 \end{aligned}\\ &\text { Maka } p=16 \sqrt{q} \end{aligned} $$
Diberi p = 32 apabila q = 4. Ungkapkan p dalam sebutan q jika
(a) p berubah secara langsung dengan q3,
(b) p berubah secara langsung dengan punca kuasa dua q.
Penyelesaian:
$$ \text { Diberi } p=32, q=4 $$
(a)
$$ \begin{aligned} &\begin{aligned} & p \alpha q^3 \\ & p=k q^3 \\ & 32=k(4)^3 \\ & k=\frac{32}{4^3} \\ & k=0.5 \end{aligned}\\ &\text { Maka } p=0.5 q^3 \end{aligned} $$
(b)
$$ \begin{aligned} &\begin{aligned} & p \alpha \sqrt{q} \\ & p=k \sqrt{q} \\ & 32=k \sqrt{4} \\ & k=\frac{32}{\sqrt{4}} \\ & =16 \end{aligned}\\ &\text { Maka } p=16 \sqrt{q} \end{aligned} $$
Soalan 4:
Gaji, RMx, yang diperoleh seorang pekerja berubah secara langsung dengan jumlah masa bekerja, t jam. Diberi bahawa seorang pekerja telah menerima gaji sebanyak RM112 selepas bekerja selama 14 jam. Tuliskan persamaan yang menghubungkan x dengan t.
Penyelesaian:
$$ \text { Diberi } x=112, t=14 $$
$$ \begin{aligned} &\begin{aligned} x & \alpha t \\ x & =k t \\ 112 & =k(14) \\ k & =\frac{112}{14} \\ k & =8 \end{aligned}\\ &\text { Maka } x=8 t \end{aligned} $$
Gaji, RMx, yang diperoleh seorang pekerja berubah secara langsung dengan jumlah masa bekerja, t jam. Diberi bahawa seorang pekerja telah menerima gaji sebanyak RM112 selepas bekerja selama 14 jam. Tuliskan persamaan yang menghubungkan x dengan t.
Penyelesaian:
$$ \text { Diberi } x=112, t=14 $$
$$ \begin{aligned} &\begin{aligned} x & \alpha t \\ x & =k t \\ 112 & =k(14) \\ k & =\frac{112}{14} \\ k & =8 \end{aligned}\\ &\text { Maka } x=8 t \end{aligned} $$