Soalan 5:
Kebarangkalian Kam Seng lulus dalam mata pelajaran Fizik dan Kimia masing-masing ialah 0.58 dan 0.42. Hitung kebarangkalian bahawa
(a) Kam Seng lulus kedua-dua mata pelajaran,
(b) Kam Seng hanya lulus satu mata pelajaran.
Penyelesaian:
(a)
$$ \begin{array}{r} \text { Diberi } P(\text { Lulus Fizik })=0.58 \\ P(\text { Lulus Kimia })=0.42 \end{array} $$
$$ \begin{aligned} \text { Maka } P(\text { Lulus Fizik dan kimia }) & =0.58 \times 0.42 \\ & =0.2436 \end{aligned} $$
(b)
$$ \begin{aligned} & P(\text { Gagal Fizik })=1-0.58=0.42 \\ & P(\text { Gagal Kimia })=1-0.42=0.58 \end{aligned} $$
$$ \begin{aligned} & \text { Maka } P \text { (Iulus satu mata pelaiaran) } \\ & =P(\text { Lulus Fizik, Gagal Kimia) }+P(\text { Lulus Kimia, Gagal Fizik }) \\ & =(0.58 \times 0.58)+(0.42 \times 0.42) \\ & =0.5128 \end{aligned} $$
Kebarangkalian Kam Seng lulus dalam mata pelajaran Fizik dan Kimia masing-masing ialah 0.58 dan 0.42. Hitung kebarangkalian bahawa
(a) Kam Seng lulus kedua-dua mata pelajaran,
(b) Kam Seng hanya lulus satu mata pelajaran.
Penyelesaian:
(a)
$$ \begin{array}{r} \text { Diberi } P(\text { Lulus Fizik })=0.58 \\ P(\text { Lulus Kimia })=0.42 \end{array} $$
$$ \begin{aligned} \text { Maka } P(\text { Lulus Fizik dan kimia }) & =0.58 \times 0.42 \\ & =0.2436 \end{aligned} $$
(b)
$$ \begin{aligned} & P(\text { Gagal Fizik })=1-0.58=0.42 \\ & P(\text { Gagal Kimia })=1-0.42=0.58 \end{aligned} $$
$$ \begin{aligned} & \text { Maka } P \text { (Iulus satu mata pelaiaran) } \\ & =P(\text { Lulus Fizik, Gagal Kimia) }+P(\text { Lulus Kimia, Gagal Fizik }) \\ & =(0.58 \times 0.58)+(0.42 \times 0.42) \\ & =0.5128 \end{aligned} $$
Soalan 6:
Fatimah menghantar surat permohonan kerja ke tiga buah syarikat. Kebarangkalian Fatimah mendapat penawaran daripada syarikat X, Y dan Z masing-masing ialah 3/5 , 4/9 dan 5/12 . Hitung kebarangkalian Fatimah mendapat penawaran daripada
(a) mana-mana dua syarikat,
(b) sekurang-kurangnya satu syarikat.
Penyelesaian:
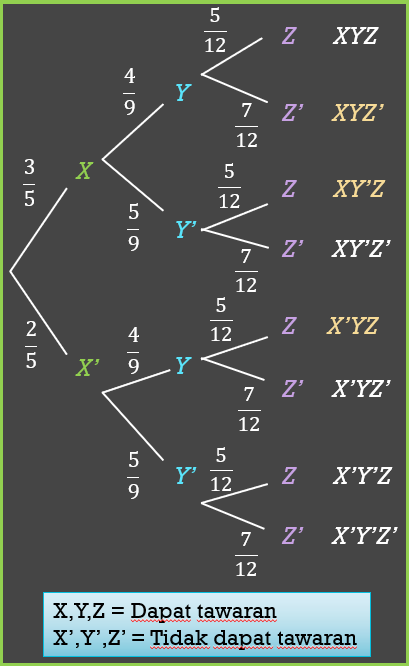
(a)
$$ \begin{aligned} P & (\text { Tawaran daripada } 2 \text { syarikat }) \\ = & P(X Y Z)+P\left(X Y^{\prime} Z\right)+P\left(X^{\prime} Y Z\right) \\ = & \left(\frac{3}{5} \times \frac{4}{9} \times \frac{7}{12}\right)+\left(\frac{3}{5} \times \frac{5}{9} \times \frac{5}{12}\right) \\ & +\left(\frac{2}{5} \times \frac{4}{9} \times \frac{5}{12}\right) \\ = & \frac{7}{45}+\frac{5}{36}+\frac{2}{27} \\ = & \frac{199}{540} \end{aligned} $$
(b)
$$ \begin{aligned} & P(\text { Sekurang-kurang } 1 \text { syarikat }) \\ & =1-P\left(X^{\prime} Y^{\prime} Z^{\prime}\right) \\ & =1-\left(\frac{2}{5} \times \frac{5}{9} \times \frac{7}{12}\right) \\ & =\frac{47}{54} \end{aligned} $$
Fatimah menghantar surat permohonan kerja ke tiga buah syarikat. Kebarangkalian Fatimah mendapat penawaran daripada syarikat X, Y dan Z masing-masing ialah 3/5 , 4/9 dan 5/12 . Hitung kebarangkalian Fatimah mendapat penawaran daripada
(a) mana-mana dua syarikat,
(b) sekurang-kurangnya satu syarikat.
Penyelesaian:

(a)
$$ \begin{aligned} P & (\text { Tawaran daripada } 2 \text { syarikat }) \\ = & P(X Y Z)+P\left(X Y^{\prime} Z\right)+P\left(X^{\prime} Y Z\right) \\ = & \left(\frac{3}{5} \times \frac{4}{9} \times \frac{7}{12}\right)+\left(\frac{3}{5} \times \frac{5}{9} \times \frac{5}{12}\right) \\ & +\left(\frac{2}{5} \times \frac{4}{9} \times \frac{5}{12}\right) \\ = & \frac{7}{45}+\frac{5}{36}+\frac{2}{27} \\ = & \frac{199}{540} \end{aligned} $$
(b)
$$ \begin{aligned} & P(\text { Sekurang-kurang } 1 \text { syarikat }) \\ & =1-P\left(X^{\prime} Y^{\prime} Z^{\prime}\right) \\ & =1-\left(\frac{2}{5} \times \frac{5}{9} \times \frac{7}{12}\right) \\ & =\frac{47}{54} \end{aligned} $$
Soalan 7:
Diberi peristiwa A dan B ialah dua peristiwa yang saling eksklusif dan P(A) = 1/3,
(a) nyatakan nilai maksimum P(B).
(b) jika P(A B) = 7/9, kenal pasti P(B).
Penyelesaian:
(a)
$$ \begin{aligned} & \text { Nilai maksimum } P(B) \\ & =1-P(A) \\ & =1-\frac{1}{3} \\ & =\frac{2}{3} \end{aligned} $$
(b)
$$ \begin{aligned} & \text { Diberi } P(A \cup B)=\frac{7}{9} \\ & \begin{aligned} & P(A)+P(B)-P(A \cap B)=\frac{7}{9} \\ & \frac{1}{3}+P(B)-0=\frac{7}{9} \\ & P(B)=\frac{7}{9}-\frac{1}{3} \\ &=\frac{4}{9} \end{aligned} \end{aligned} $$
Diberi peristiwa A dan B ialah dua peristiwa yang saling eksklusif dan P(A) = 1/3,
(a) nyatakan nilai maksimum P(B).
(b) jika P(A B) = 7/9, kenal pasti P(B).
Penyelesaian:
(a)
$$ \begin{aligned} & \text { Nilai maksimum } P(B) \\ & =1-P(A) \\ & =1-\frac{1}{3} \\ & =\frac{2}{3} \end{aligned} $$
(b)
$$ \begin{aligned} & \text { Diberi } P(A \cup B)=\frac{7}{9} \\ & \begin{aligned} & P(A)+P(B)-P(A \cap B)=\frac{7}{9} \\ & \frac{1}{3}+P(B)-0=\frac{7}{9} \\ & P(B)=\frac{7}{9}-\frac{1}{3} \\ &=\frac{4}{9} \end{aligned} \end{aligned} $$
Soalan 8:
Kotak R mengandungi lima biji guli merah dan tujuh biji guli hijau manakala kotak T mengandungi empat biji guli merah dan lapan biji guli hijau. Sebiji guli dipilih secara rawak dari kotak R. Sekiranya guli itu berwarna merah, guli itu akan dimasukkan ke dalam kotak T. Sekiranya guli itu berwarna hijau, guli itu akan dikembalikan ke dalam kotak R. Seterusnya sebiji guli akan dipilih secara rawak dari kotak T. Warna guli yang dipilih akan dicatat.
(a) Hitung kebarangkalian
(i) kedua-dua biji guli yang dipilih berwarna merah,
(ii) kedua-dua biji guli yang dipilih berlainan warna.
(b) Kelas 4 Amanah mempunyai 36 orang murid. Sekiranya setiap murid daripada 4 Amanah diberi peluang memilih dua biji guli dengan keadaan seperti yang dinyatakan dan murid yang berjaya memilih dua biji guli yang berwarna hijau akan diberi hadiah bernilai RM5, anggarkan kos hadiah yang diperlukan.
Penyelesaian:
$$ \begin{aligned} &\text { Pada Kotak } R \text {, }\\ &P(M)=\frac{5}{12}, P(H)=\frac{7}{12} \end{aligned} $$
$$ \begin{aligned} &\text { Pada Kotak T, }\\ &P(M)=\frac{4}{12}, P(H)=\frac{8}{12} \end{aligned} $$
(a)
$$ \begin{aligned} P(M, M) & =\frac{5}{12} \times \frac{5}{13} \\ & =\frac{25}{156} \end{aligned} $$
(b)
$$ \begin{aligned} & P(M, H)+P(H, M) \\ & =\left(\frac{5}{12} \times \frac{8}{13}\right)+\left(\frac{7}{12} \times \frac{4}{12}\right) \\ & =\frac{10}{39}+\frac{7}{36} \\ & =\frac{211}{468} \end{aligned} $$
(c)
$$ \begin{aligned} P(H, H) & =\frac{7}{12} \times \frac{8}{12} \\ & =\frac{7}{18} \end{aligned} $$
$$ \begin{aligned} &\text { Kos hadiah bagi Kelas } 4 \text { Amanah }\\ &\begin{aligned} & =36 \times \frac{7}{18} \times R M 5 \\ & =R M 70 \end{aligned} \end{aligned} $$
Kotak R mengandungi lima biji guli merah dan tujuh biji guli hijau manakala kotak T mengandungi empat biji guli merah dan lapan biji guli hijau. Sebiji guli dipilih secara rawak dari kotak R. Sekiranya guli itu berwarna merah, guli itu akan dimasukkan ke dalam kotak T. Sekiranya guli itu berwarna hijau, guli itu akan dikembalikan ke dalam kotak R. Seterusnya sebiji guli akan dipilih secara rawak dari kotak T. Warna guli yang dipilih akan dicatat.
(a) Hitung kebarangkalian
(i) kedua-dua biji guli yang dipilih berwarna merah,
(ii) kedua-dua biji guli yang dipilih berlainan warna.
(b) Kelas 4 Amanah mempunyai 36 orang murid. Sekiranya setiap murid daripada 4 Amanah diberi peluang memilih dua biji guli dengan keadaan seperti yang dinyatakan dan murid yang berjaya memilih dua biji guli yang berwarna hijau akan diberi hadiah bernilai RM5, anggarkan kos hadiah yang diperlukan.
Penyelesaian:
$$ \begin{aligned} &\text { Pada Kotak } R \text {, }\\ &P(M)=\frac{5}{12}, P(H)=\frac{7}{12} \end{aligned} $$
$$ \begin{aligned} &\text { Pada Kotak T, }\\ &P(M)=\frac{4}{12}, P(H)=\frac{8}{12} \end{aligned} $$
(a)
$$ \begin{aligned} P(M, M) & =\frac{5}{12} \times \frac{5}{13} \\ & =\frac{25}{156} \end{aligned} $$
(b)
$$ \begin{aligned} & P(M, H)+P(H, M) \\ & =\left(\frac{5}{12} \times \frac{8}{13}\right)+\left(\frac{7}{12} \times \frac{4}{12}\right) \\ & =\frac{10}{39}+\frac{7}{36} \\ & =\frac{211}{468} \end{aligned} $$
(c)
$$ \begin{aligned} P(H, H) & =\frac{7}{12} \times \frac{8}{12} \\ & =\frac{7}{18} \end{aligned} $$
$$ \begin{aligned} &\text { Kos hadiah bagi Kelas } 4 \text { Amanah }\\ &\begin{aligned} & =36 \times \frac{7}{18} \times R M 5 \\ & =R M 70 \end{aligned} \end{aligned} $$