5.5 Garis Selari


5.5 Garis Selari

(A) Kecerunan Garis Selari
1.   Dua garis adalah selari jika kecerunannya adalah sama.
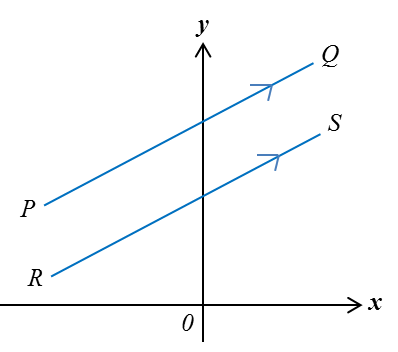
Jika PQ // RS,
maka mPQ = mRS



2.   Jika dua garis lurus mempunyai kecerunan yang sama, maka pasangan garis lurus tersebut adalah selari.
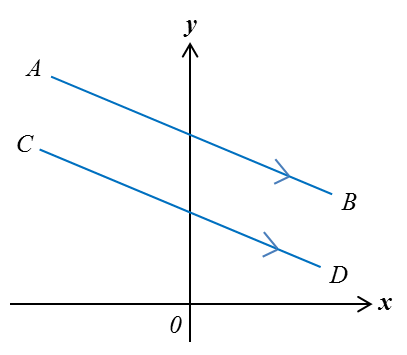
Jika mAB = mCD
maka AB // CD



Contoh 1:
Tentukan sama ada setiap pasangan garis lurus berikut adalah selari atau tidak.
(a)  2y – 4x = 6
y = 2x – 5
(b)  2y = 3x – 4
3y = 2x + 12

Penyelesaian:
(a)
2y – 4x = 6
2y = 6 + 4x
y = 2x + 3,   m1= 2
y = 2x – 5,   m2 = 2
m1 = m2
Maka, dua garis lurus adalah selari.

(b)
2 y = 3 x − 4 y = 3 2 x − 2 , m 1 = 3 2 3 y = 2 x + 12 y = 2 3 x + 4 , m 2 = 2 3 m 1 ≠ m 2 ∴ Maka, dua garis lurus adalah tidak selari .


(B) Persamaan Garis Selari
Langkah-langkah berikut diambil untuk mencari persamaan garis lurus yang melalui satu titik dan selari dengan garis lurus yang lain:

Langkah 1: Menyusun persamaan garis lurus dalam bentuk y = mx + c.

Langkah 2: Cari kecerunan garis lurus daripada persamaan garis lurus yang selari dengannya.

Langkah 3: Gantikan nilai kecerunan, m, koordinat-x dan koordinat-y bagi titik yang diberi ke dalam persamaan y = mx + c untuk mencari nilai pintasan-y, c.

Langkah 4: Tulis persamaan garis lurus dalam bentuk y = mx + c.


Contoh 2:
Cari persamaan bagi garis lurus yang melalui titik (–8, 2) dan selari dengan garis lurus
4y + 3x = 12.

Penyelesaian:
4 y + 3 x = 12 4 y = − 3 x + 12 y = − 3 4 x + 3 ∴ m = − 3 4

Pada (−8,2),  gantikan m=− 3 4 , x=−8, y=2 ke dalam: y=mx+c 2=− 3 4 ( −8 )+c c=2−6 c=−4 ∴ Persamaan garis lurus ialah y=− 3 4 x−4.


Leave a Comment