Soalan 1:
Tentukan julat dan julat antara kuartil bagi setiap set data berikut.
(a) 3, 7, 5, 9, 4, 4, 8, 7, 6, 2, 5.
(b) 13, 15, 19, 22, 17, 14, 15, 16, 18, 19, 11, 10, 20.
(c) 2.3, 2.2, 3.1, 2.8, 2.7, 2.4, 2.5, 2.3.
Penyelesaian:
(a)
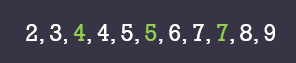
$$ \begin{aligned} & \text { Julat }=9-2=7 \\ & \begin{aligned} \text { Julat antara kuartil } & =Q_3-Q_1 \\ & =7-4 \\ & =3 \end{aligned} \end{aligned} $$
(b)

$$ \begin{aligned} & \text { Julat }=22-10=12 \\ & \begin{aligned} \text { Julat antara kuartil } & =19-\left(\frac{13+14}{2}\right) \\ & =5.5 \end{aligned} \end{aligned} $$
(c)
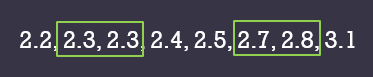
$$ \begin{aligned} & \text { Julat }=3.1-2.2=0.9 \\ & \begin{aligned} \text { Julat antara kuartil } & =\left(\frac{2.7+2.8}{2}\right)-2.3 \\ & =0.45 \end{aligned} \end{aligned} $$
Tentukan julat dan julat antara kuartil bagi setiap set data berikut.
(a) 3, 7, 5, 9, 4, 4, 8, 7, 6, 2, 5.
(b) 13, 15, 19, 22, 17, 14, 15, 16, 18, 19, 11, 10, 20.
(c) 2.3, 2.2, 3.1, 2.8, 2.7, 2.4, 2.5, 2.3.
Penyelesaian:
(a)

$$ \begin{aligned} & \text { Julat }=9-2=7 \\ & \begin{aligned} \text { Julat antara kuartil } & =Q_3-Q_1 \\ & =7-4 \\ & =3 \end{aligned} \end{aligned} $$
(b)

$$ \begin{aligned} & \text { Julat }=22-10=12 \\ & \begin{aligned} \text { Julat antara kuartil } & =19-\left(\frac{13+14}{2}\right) \\ & =5.5 \end{aligned} \end{aligned} $$
(c)

$$ \begin{aligned} & \text { Julat }=3.1-2.2=0.9 \\ & \begin{aligned} \text { Julat antara kuartil } & =\left(\frac{2.7+2.8}{2}\right)-2.3 \\ & =0.45 \end{aligned} \end{aligned} $$
Soalan 2:
Tentukan julat dan julat antara kuartil bagi setiap set data berikut.
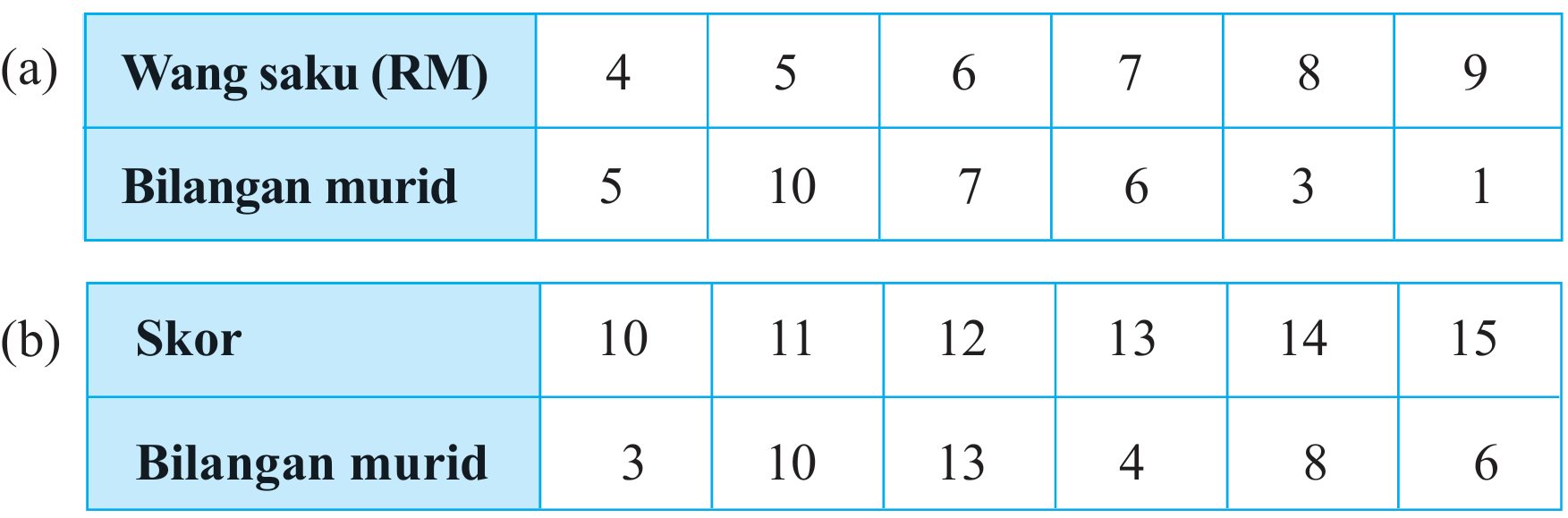
Penyelesaian:
(a)
Julat = 9 – 4 = 5
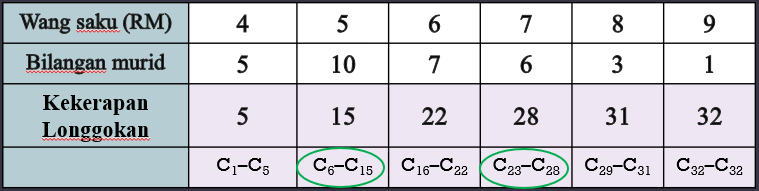
$$ \begin{aligned} & Q_1=\frac{1}{4} \times 32=\text { cerapan ke }-8 \\ & Q_3=\frac{3}{4} \times 32=\text { cerapan ke }-24 \end{aligned} $$
$$ \begin{aligned} \text { Julat antara kuartil } & =Q_3-Q_1 \\ & =7-5 \\ & =2 \end{aligned} $$
(b)
Julat = 15 – 10 = 5
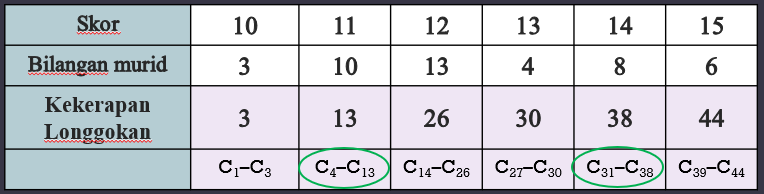
$$ \begin{aligned} & Q_1=\frac{1}{4} \times 44=\text { cerapan ke }-11 \\ & Q_3=\frac{3}{4} \times 44=\text { cerapan ke }-33 \end{aligned} $$
$$ \begin{aligned} \text { Julat antara kuartil } & =Q_3-Q_1 \\ & =14-11 \\ & =3 \end{aligned} $$
Tentukan julat dan julat antara kuartil bagi setiap set data berikut.

Penyelesaian:
(a)
Julat = 9 – 4 = 5

$$ \begin{aligned} & Q_1=\frac{1}{4} \times 32=\text { cerapan ke }-8 \\ & Q_3=\frac{3}{4} \times 32=\text { cerapan ke }-24 \end{aligned} $$
$$ \begin{aligned} \text { Julat antara kuartil } & =Q_3-Q_1 \\ & =7-5 \\ & =2 \end{aligned} $$
(b)
Julat = 15 – 10 = 5

$$ \begin{aligned} & Q_1=\frac{1}{4} \times 44=\text { cerapan ke }-11 \\ & Q_3=\frac{3}{4} \times 44=\text { cerapan ke }-33 \end{aligned} $$
$$ \begin{aligned} \text { Julat antara kuartil } & =Q_3-Q_1 \\ & =14-11 \\ & =3 \end{aligned} $$
Soalan 3:
Bagi setiap set data berikut, tentukan varians dan sisihan piawai.
(a) 5, 7, 6, 9, 12, 10, 10, 13
(b) 32, 40, 35, 39, 44, 48, 42
Penyelesaian:
(a)
$$ \begin{aligned} \operatorname{Min} & =\frac{5+7+6+9+12+10+10+13}{8} \\ & =9 \end{aligned} $$
$$ \begin{aligned} &\text { Varians, } \sigma^2=\frac{\sum x^2}{N}-(\bar{x})^2\\ &\begin{aligned} & =\frac{5^2+7^2+6^2+9^2+12^2+10^2+10^2+13^2}{8}-9^2 \\ & =7 \end{aligned} \end{aligned} $$
$$ \text { Sisihan piawai, } \begin{aligned} \sigma & =\sqrt{7} \\ & =2.646 \end{aligned} $$
(b)
$$ \begin{aligned} \operatorname{Min} & =\frac{32+40+35+39+44+48+42}{7} \\ & =40 \end{aligned} $$
$$ \begin{aligned} &\text { Varians, } \sigma^2=\frac{\sum x^2}{N}-(\bar{x})^2\\ &\begin{aligned} & =\frac{32^2+40^2+35^2+39^2+44^2+48^2+42^2}{7}-40^2 \\ & =24.86 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Sisihan piawai, } \sigma=\sqrt{24.86}\\ &=4.986 \end{aligned} $$
Bagi setiap set data berikut, tentukan varians dan sisihan piawai.
(a) 5, 7, 6, 9, 12, 10, 10, 13
(b) 32, 40, 35, 39, 44, 48, 42
Penyelesaian:
(a)
$$ \begin{aligned} \operatorname{Min} & =\frac{5+7+6+9+12+10+10+13}{8} \\ & =9 \end{aligned} $$
$$ \begin{aligned} &\text { Varians, } \sigma^2=\frac{\sum x^2}{N}-(\bar{x})^2\\ &\begin{aligned} & =\frac{5^2+7^2+6^2+9^2+12^2+10^2+10^2+13^2}{8}-9^2 \\ & =7 \end{aligned} \end{aligned} $$
$$ \text { Sisihan piawai, } \begin{aligned} \sigma & =\sqrt{7} \\ & =2.646 \end{aligned} $$
(b)
$$ \begin{aligned} \operatorname{Min} & =\frac{32+40+35+39+44+48+42}{7} \\ & =40 \end{aligned} $$
$$ \begin{aligned} &\text { Varians, } \sigma^2=\frac{\sum x^2}{N}-(\bar{x})^2\\ &\begin{aligned} & =\frac{32^2+40^2+35^2+39^2+44^2+48^2+42^2}{7}-40^2 \\ & =24.86 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Sisihan piawai, } \sigma=\sqrt{24.86}\\ &=4.986 \end{aligned} $$
Soalan 4:
Jadual berikut menunjukkan bilangan gol yang diperoleh oleh 20 orang pemain bola sepak dalam suatu pertandingan. Tentukan varians dan sisihan piawai bagi taburan ini.

Penyelesaian:

$$ \begin{aligned} \operatorname{Min}, \bar{x} & =\frac{\sum f x}{\sum f} \\ & =\frac{3(0)+5(1)+6(2)+5(3)+1(4)}{20} \\ & =1.8 \end{aligned} $$
$$ \begin{aligned} &\text { Varians, }\\ &\begin{aligned} \sigma^2 & =\frac{\sum f x^2}{\sum f}-(\bar{x})^2 \\ & =\frac{3(0)^2+5(1)^2+6(2)^2+5(3)^2+1(4)^2}{20}-1.8^2 \\ & =1.26 \end{aligned} \end{aligned} $$
$$ \text { Sisihan piawai, } \begin{aligned} \sigma & =\sqrt{1.26} \\ & =1.122 \end{aligned} $$
Jadual berikut menunjukkan bilangan gol yang diperoleh oleh 20 orang pemain bola sepak dalam suatu pertandingan. Tentukan varians dan sisihan piawai bagi taburan ini.

Penyelesaian:

$$ \begin{aligned} \operatorname{Min}, \bar{x} & =\frac{\sum f x}{\sum f} \\ & =\frac{3(0)+5(1)+6(2)+5(3)+1(4)}{20} \\ & =1.8 \end{aligned} $$
$$ \begin{aligned} &\text { Varians, }\\ &\begin{aligned} \sigma^2 & =\frac{\sum f x^2}{\sum f}-(\bar{x})^2 \\ & =\frac{3(0)^2+5(1)^2+6(2)^2+5(3)^2+1(4)^2}{20}-1.8^2 \\ & =1.26 \end{aligned} \end{aligned} $$
$$ \text { Sisihan piawai, } \begin{aligned} \sigma & =\sqrt{1.26} \\ & =1.122 \end{aligned} $$