Soalan 1:
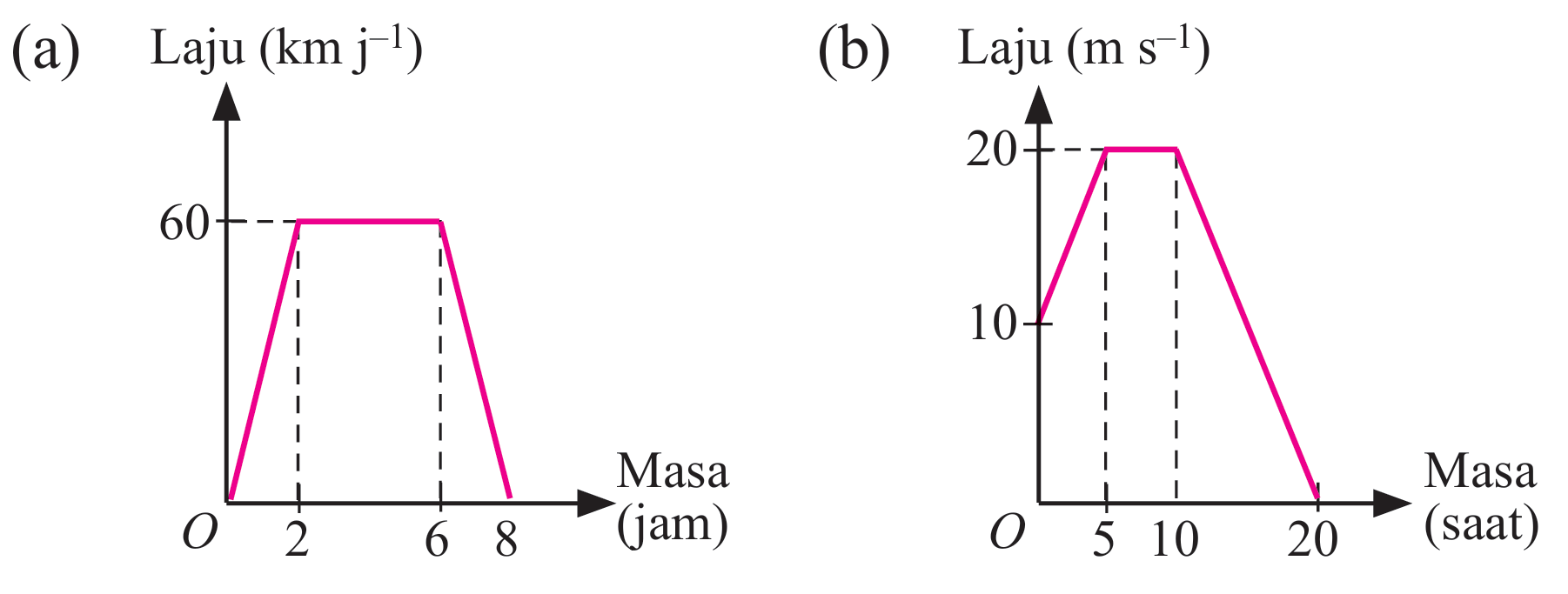
Hitung jarak, dalam km, yang dilalui oleh setiap gerakan berdasarkan graf laju-masa yang diberikan.
Penyelesaian:
(a)
$$ \begin{aligned} \text { Jarak yang dilalui } & =\text { Luas di bawah graf } \\ & =\text { Luas trapizium } \\ & =\frac{1}{2} \times[(6-2)+8] j \times 60 \mathrm{kmj}^{-1} \\ & =360 \mathrm{~km} \end{aligned} $$
(b)
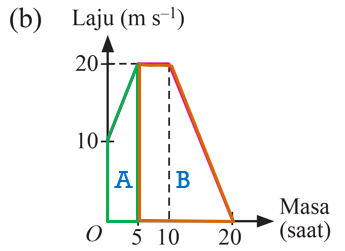
$$ \begin{aligned} & \text { Jarak yang dilalui }=\text { Luas trapezium } A+\text { Luas trapezium B } \\ & =\left[\frac{1}{2} \times(10+20) \mathrm{ms}^{-1} \times 5 \mathrm{~s}\right]+\left[\frac{1}{2} \times[(10-5)+(20-5)] \mathrm{s} \times 20 \mathrm{~ms}^{-1}\right] \\ & =75 \mathrm{~m}+200 \mathrm{~m} \\ & =275 \mathrm{~m} \\ & =0.275 \mathrm{~km} \end{aligned} $$
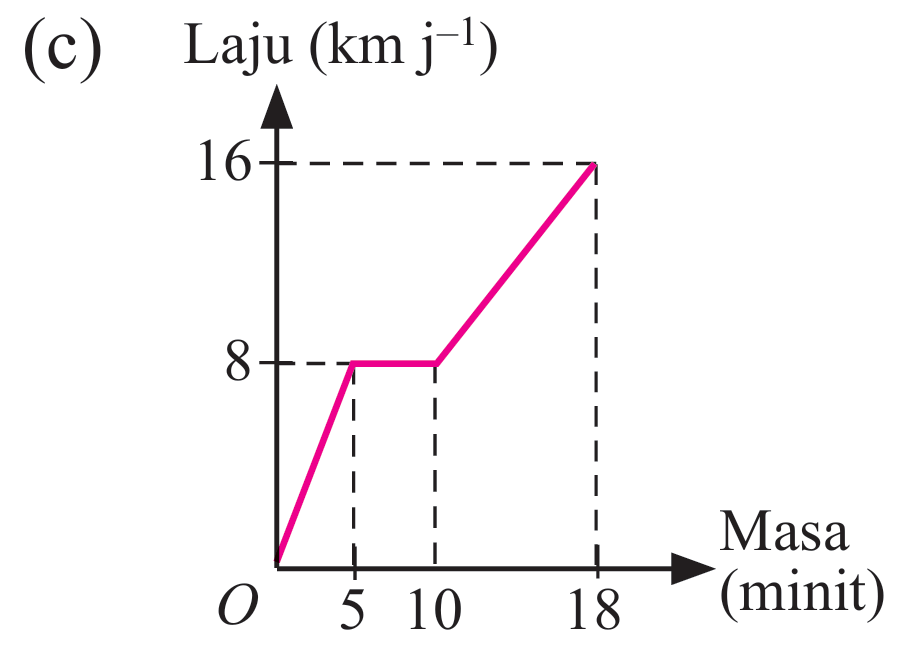
(c)
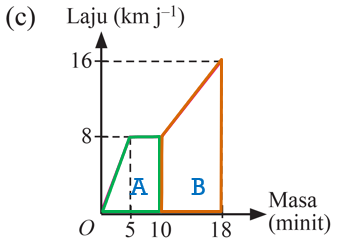
$$ \begin{aligned} & \text { Jarak yang dilalui }=\text { Luas trapezium } A+\text { Luas trapezium B } \\ & =\left[\frac{1}{2} \times[(10-5)+10] \mathrm{min} \times 8 \mathrm{kmj}^{-1}\right]+\left[\frac{1}{2} \times(8+16) \mathrm{kmj}^{-1} \times(18-10) \mathrm{min}\right] \\ & =\left[4 \mathrm{kmj}^{-1} \times \frac{15}{60} j\right]+\left[12 \mathrm{kmj}^{-1} \times \frac{8}{60} j\right] \\ & =(1+1.6) \mathrm{km} \\ & =2.6 \mathrm{~km} \end{aligned} $$
Hitung jarak, dalam km, yang dilalui oleh setiap gerakan berdasarkan graf laju-masa yang diberikan.


Penyelesaian:
(a)
$$ \begin{aligned} \text { Jarak yang dilalui } & =\text { Luas di bawah graf } \\ & =\text { Luas trapizium } \\ & =\frac{1}{2} \times[(6-2)+8] j \times 60 \mathrm{kmj}^{-1} \\ & =360 \mathrm{~km} \end{aligned} $$
(b)

$$ \begin{aligned} & \text { Jarak yang dilalui }=\text { Luas trapezium } A+\text { Luas trapezium B } \\ & =\left[\frac{1}{2} \times(10+20) \mathrm{ms}^{-1} \times 5 \mathrm{~s}\right]+\left[\frac{1}{2} \times[(10-5)+(20-5)] \mathrm{s} \times 20 \mathrm{~ms}^{-1}\right] \\ & =75 \mathrm{~m}+200 \mathrm{~m} \\ & =275 \mathrm{~m} \\ & =0.275 \mathrm{~km} \end{aligned} $$
(c)

$$ \begin{aligned} & \text { Jarak yang dilalui }=\text { Luas trapezium } A+\text { Luas trapezium B } \\ & =\left[\frac{1}{2} \times[(10-5)+10] \mathrm{min} \times 8 \mathrm{kmj}^{-1}\right]+\left[\frac{1}{2} \times(8+16) \mathrm{kmj}^{-1} \times(18-10) \mathrm{min}\right] \\ & =\left[4 \mathrm{kmj}^{-1} \times \frac{15}{60} j\right]+\left[12 \mathrm{kmj}^{-1} \times \frac{8}{60} j\right] \\ & =(1+1.6) \mathrm{km} \\ & =2.6 \mathrm{~km} \end{aligned} $$
Soalan 2:
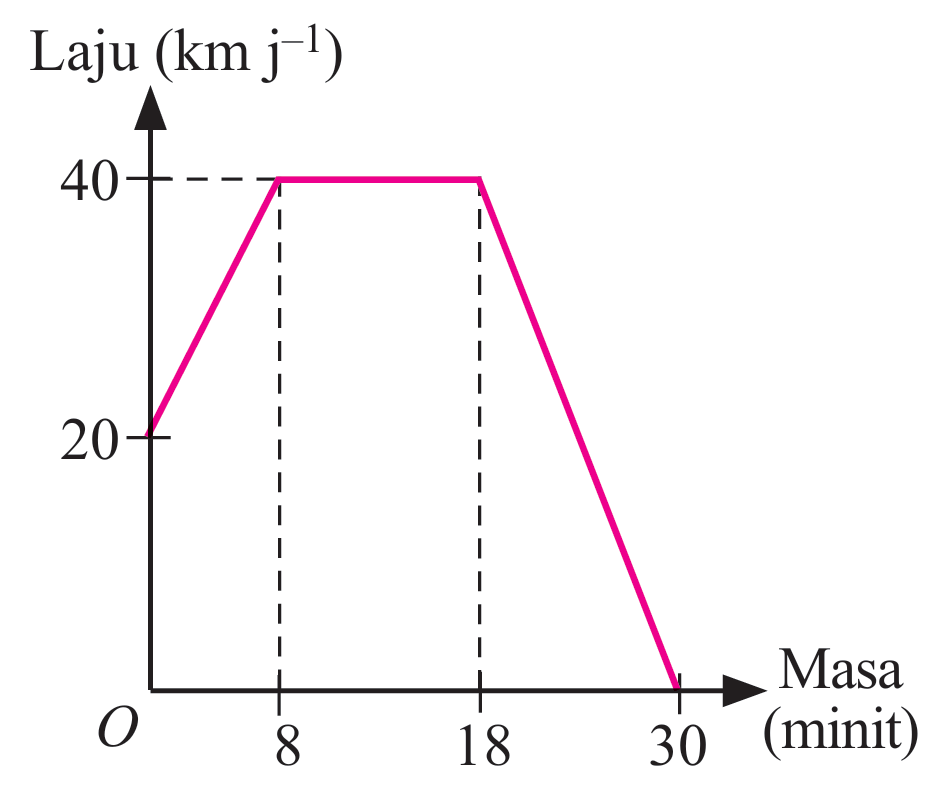
Graf laju-masa di sebelah menunjukkan kelajuan motosikal Encik Mustaffa untuk tempoh masa 30 minit semasa menjemput anaknya dari kelas tambahan. Hitung,
(a) jumlah jarak, dalam km, yang dilalui dalam tempoh 30 minit.
(b) laju purata, dalam km j–1, motosikal Encik Mustaffa untuk tempoh 30 minit.
Penyelesaian:
(a)
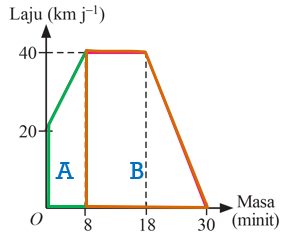
$$ \begin{aligned} & \text { Jumlah jarak yang dilalui }=\text { Luas trapizium } \mathrm{A}+\text { Luas trapizium B } \\ & =\left[\frac{1}{2} \times(20+40) \mathrm{kmj}^{-1} \times 8 \mathrm{~min}\right]+\left[\frac{1}{2} \times[(18-8)+(30-8)] \mathrm{min} \times 40 \mathrm{kmj}^{-1}\right] \\ & =\left[\frac{1}{2} \times 60 \mathrm{kmj}^{-1} \times \frac{8}{60} j\right]+\left[\frac{1}{2} \times \frac{32}{60} j \times 40 \mathrm{kmj}^{-1}\right] \\ & =\left(4+10 \frac{2}{3}\right) \mathrm{km} \\ & =14 \frac{2}{3} \mathrm{~km} \end{aligned} $$
(b)
$$ \begin{aligned} \text { Laju purata } & =\frac{\text { Jumlah jarak }}{\text { Jumlah masa }} \\ & =\frac{14 \frac{2}{3} \mathrm{~km}}{30 \mathrm{~min}} \\ & =\frac{14 \frac{2}{3} \mathrm{~km}}{\left(\frac{30}{60}\right) \mathrm{j}} \\ & =29 \frac{1}{3} \mathrm{kmj}^{-1} \end{aligned} $$

Graf laju-masa di sebelah menunjukkan kelajuan motosikal Encik Mustaffa untuk tempoh masa 30 minit semasa menjemput anaknya dari kelas tambahan. Hitung,
(a) jumlah jarak, dalam km, yang dilalui dalam tempoh 30 minit.
(b) laju purata, dalam km j–1, motosikal Encik Mustaffa untuk tempoh 30 minit.
Penyelesaian:
(a)

$$ \begin{aligned} & \text { Jumlah jarak yang dilalui }=\text { Luas trapizium } \mathrm{A}+\text { Luas trapizium B } \\ & =\left[\frac{1}{2} \times(20+40) \mathrm{kmj}^{-1} \times 8 \mathrm{~min}\right]+\left[\frac{1}{2} \times[(18-8)+(30-8)] \mathrm{min} \times 40 \mathrm{kmj}^{-1}\right] \\ & =\left[\frac{1}{2} \times 60 \mathrm{kmj}^{-1} \times \frac{8}{60} j\right]+\left[\frac{1}{2} \times \frac{32}{60} j \times 40 \mathrm{kmj}^{-1}\right] \\ & =\left(4+10 \frac{2}{3}\right) \mathrm{km} \\ & =14 \frac{2}{3} \mathrm{~km} \end{aligned} $$
(b)
$$ \begin{aligned} \text { Laju purata } & =\frac{\text { Jumlah jarak }}{\text { Jumlah masa }} \\ & =\frac{14 \frac{2}{3} \mathrm{~km}}{30 \mathrm{~min}} \\ & =\frac{14 \frac{2}{3} \mathrm{~km}}{\left(\frac{30}{60}\right) \mathrm{j}} \\ & =29 \frac{1}{3} \mathrm{kmj}^{-1} \end{aligned} $$
Soalan 3:
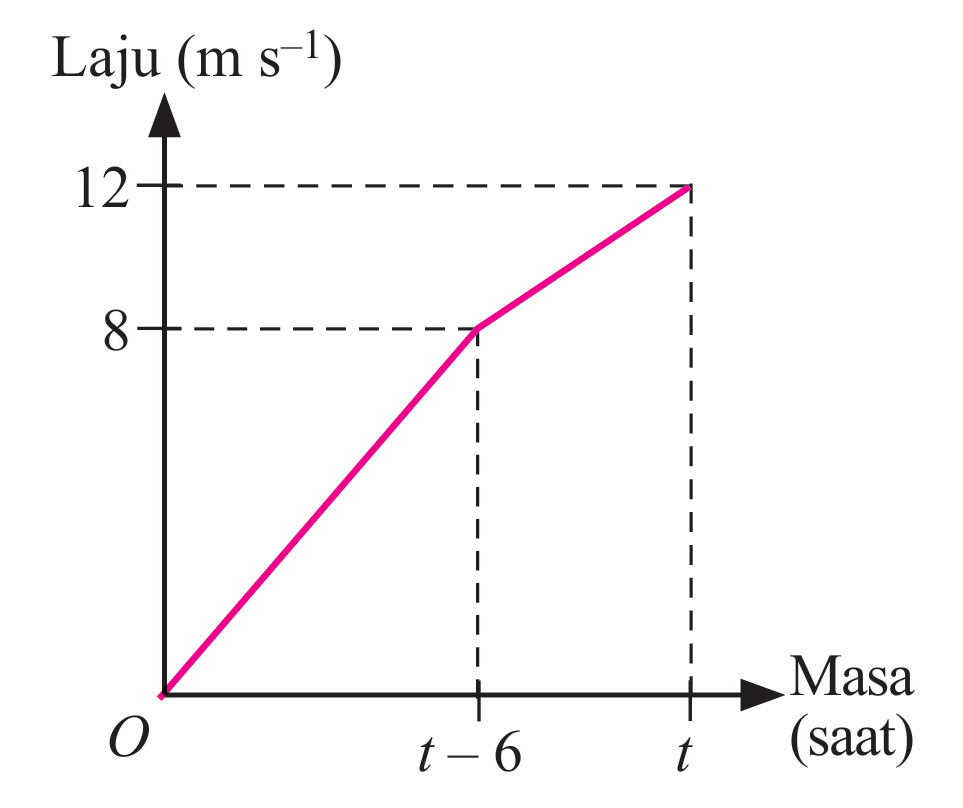
Sarves menyertai pertandingan larian 100 m semasa kejohanan olahraga di sekolahnya. Graf laju-masa di sebelah menunjukkan kelajuan larian Sarves sehingga garisan penamat. Hitung,
(a) nilai t.
(b) laju purata larian Sarves dalam km j–1.
Penyelesaian:
(a)
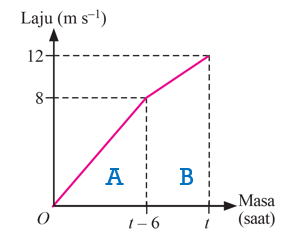
$$ \begin{aligned} \text { Jumlah jarak yang dilalui } & =\text { Luas di bawah graf }(\mathrm{A}+\mathrm{B}) \\ & =\text { Luas segi tiga }+ \text { Luas trapizium } \end{aligned} $$
$$ \begin{aligned} & {\left[\frac{1}{2} \times(t-6) s \times 8 \mathrm{~ms}^{-1}\right]+\left[\frac{1}{2} \times(8+12) \mathrm{ms}^{-1} \times[\mathrm{t}-(\mathrm{t}-6)] \mathrm{s}\right]=100 \mathrm{~m} } \\ & 4(t-6)+(10 \times 6)=100 \\ & 4 t-24+60=100 \\ & 4 t+36=100 \\ & 4 t=64 \\ & t=16 \mathrm{~s} \end{aligned} $$
(b)
$$ \begin{aligned} \text { Laju purata } & =\frac{\text { Jumlah jarak }}{\text { Jumlah masa }} \\ & =\frac{100 \mathrm{~m}}{16 \mathrm{~s}} \\ & =\frac{\left(\frac{100}{1000}\right) \mathrm{km}}{\left(\frac{16}{3600}\right) j} \\ & =\left(\frac{100}{1000}\right) \mathrm{km} \times\left(\frac{3600}{16}\right) j \\ & =22.5 \mathrm{kmj}^{-1} \end{aligned} $$

Sarves menyertai pertandingan larian 100 m semasa kejohanan olahraga di sekolahnya. Graf laju-masa di sebelah menunjukkan kelajuan larian Sarves sehingga garisan penamat. Hitung,
(a) nilai t.
(b) laju purata larian Sarves dalam km j–1.
Penyelesaian:
(a)

$$ \begin{aligned} \text { Jumlah jarak yang dilalui } & =\text { Luas di bawah graf }(\mathrm{A}+\mathrm{B}) \\ & =\text { Luas segi tiga }+ \text { Luas trapizium } \end{aligned} $$
$$ \begin{aligned} & {\left[\frac{1}{2} \times(t-6) s \times 8 \mathrm{~ms}^{-1}\right]+\left[\frac{1}{2} \times(8+12) \mathrm{ms}^{-1} \times[\mathrm{t}-(\mathrm{t}-6)] \mathrm{s}\right]=100 \mathrm{~m} } \\ & 4(t-6)+(10 \times 6)=100 \\ & 4 t-24+60=100 \\ & 4 t+36=100 \\ & 4 t=64 \\ & t=16 \mathrm{~s} \end{aligned} $$
(b)
$$ \begin{aligned} \text { Laju purata } & =\frac{\text { Jumlah jarak }}{\text { Jumlah masa }} \\ & =\frac{100 \mathrm{~m}}{16 \mathrm{~s}} \\ & =\frac{\left(\frac{100}{1000}\right) \mathrm{km}}{\left(\frac{16}{3600}\right) j} \\ & =\left(\frac{100}{1000}\right) \mathrm{km} \times\left(\frac{3600}{16}\right) j \\ & =22.5 \mathrm{kmj}^{-1} \end{aligned} $$