Soalan 14:
Kedalaman air dalam sebuah tadahan air berubah mengikut masa. Apabila tinggi air mencapai paras maksimum, pintu air akan terbuka untuk melepaskan air keluar sehingga paras air kembali ke paras minimum. Rajah 8 menunjukkan satu kitaran lengkap kedalaman air, dalam m, dalam tadahan air itu.
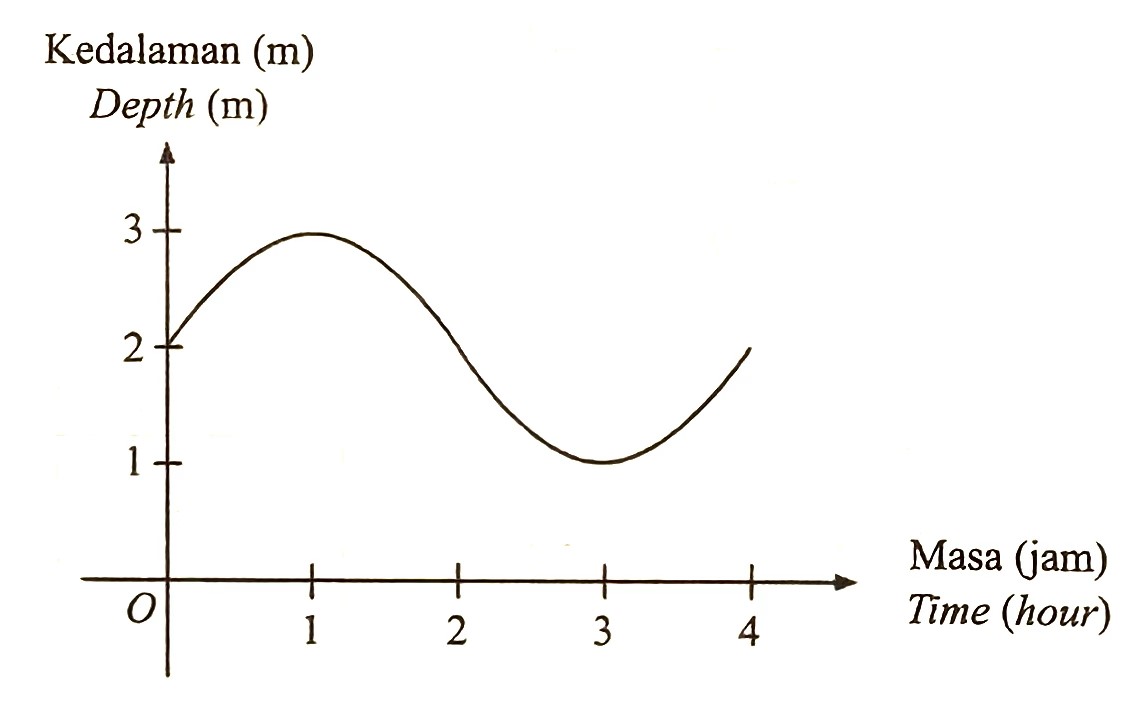
(a) Berdasarkan Rajah 8, nyatakan
(i) paras minimum, dalam m , air dalam tadahan air itu. [1 markah]
(ii) jangka masa, dalam jam, pintu tadahan air itu dibuka. [1 markah]
(c) Pada musim huian, kedalaman air akan meningkat dari paras awal ke paras maksimum lebih cepat. Satu kitaran lengkap akan berlaku setiap 2 jam.
(i) Lengkapkan graf di ruang jawapan untuk kedalaman air semasa musim huian. [2 markah]
(ii) Seterusnya, dengan membandingkan Rajah 8 dengan graf anda di (c)(i), jelaskan apakah maksud perbezaan frekuensi keduadua graf dalam konteks soalan tersebut. [1 markah]
Penyelesaian:
(a)(i) Daripada graf, paras minimum ialah 1 m.
(a)(ii)
Daripada graf, jangka masa pintu tadahan air itu dibuka
= 3 – 1
= 2 jam
(b)(i)
$$ \begin{aligned} &y=a \sin b x+c\\ &\text { Amplitud, } a=1 \end{aligned} $$
$$ \begin{aligned} &b=\frac{360}{4}=90\\ &c=2 \text {, graf gerak } 2 \text { unit ke atas }\\ &\begin{aligned} & y=(1) \sin (90) x+2 \\ & y=\sin 90 x+2 \end{aligned} \end{aligned} $$
(b)(ii)
$$ x=150 \text { minit }=\frac{150}{60}=2.5 \text { jam } $$
$$ \begin{aligned} y & =\sin 90(2.5)+2 \\ & =-0.7071+2 \\ & =1.2929 \mathrm{~m} \end{aligned} $$
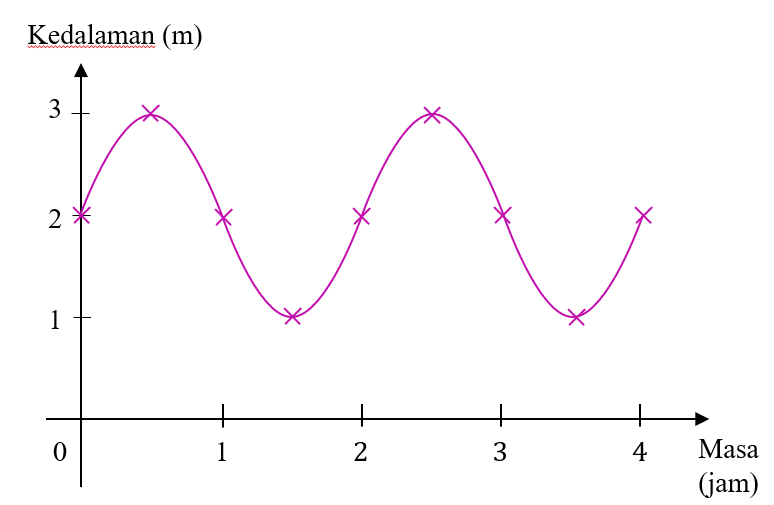
(c)(i)
Diberi satu kitaran lengkap akan berlaku setiap 2 jam
$$ \begin{aligned} & b=\frac{360}{2}=180 \\ & y=\sin 180 x+2 \end{aligned} $$
$$ \begin{aligned} & y=\sin 180(0)+2 \\ & y=0+2=2 \end{aligned} $$
$$ \begin{aligned} & y=\sin 180(0.5)+2 \\ & y=1+2=3 \end{aligned} $$
$$ \begin{aligned} & y=\sin 180(1)+2 \\ & y=0+2=2 \end{aligned} $$
$$ \begin{aligned} & y=\sin 180(1.5)+2 \\ & y=-1+2=1 \end{aligned} $$

Kedalaman air dalam sebuah tadahan air berubah mengikut masa. Apabila tinggi air mencapai paras maksimum, pintu air akan terbuka untuk melepaskan air keluar sehingga paras air kembali ke paras minimum. Rajah 8 menunjukkan satu kitaran lengkap kedalaman air, dalam m, dalam tadahan air itu.

(a) Berdasarkan Rajah 8, nyatakan
(i) paras minimum, dalam m , air dalam tadahan air itu. [1 markah]
(ii) jangka masa, dalam jam, pintu tadahan air itu dibuka. [1 markah]
(b) (i) Tulis persamaan bagi graf tersebut dalam bentuk dengan keadaan dan adalah pemalar. [2 markah]
(ii) Seterusnya, cari kedalaman air, dalam m, apabila masa ialah 150 minit.
[1 markah]
(c) Pada musim huian, kedalaman air akan meningkat dari paras awal ke paras maksimum lebih cepat. Satu kitaran lengkap akan berlaku setiap 2 jam.
(i) Lengkapkan graf di ruang jawapan untuk kedalaman air semasa musim huian. [2 markah]
(ii) Seterusnya, dengan membandingkan Rajah 8 dengan graf anda di (c)(i), jelaskan apakah maksud perbezaan frekuensi keduadua graf dalam konteks soalan tersebut. [1 markah]
Penyelesaian:
(a)(i) Daripada graf, paras minimum ialah 1 m.
(a)(ii)
Daripada graf, jangka masa pintu tadahan air itu dibuka
= 3 – 1
= 2 jam
(b)(i)
$$ \begin{aligned} &y=a \sin b x+c\\ &\text { Amplitud, } a=1 \end{aligned} $$
$$ \begin{aligned} &b=\frac{360}{4}=90\\ &c=2 \text {, graf gerak } 2 \text { unit ke atas }\\ &\begin{aligned} & y=(1) \sin (90) x+2 \\ & y=\sin 90 x+2 \end{aligned} \end{aligned} $$
(b)(ii)
$$ x=150 \text { minit }=\frac{150}{60}=2.5 \text { jam } $$
$$ \begin{aligned} y & =\sin 90(2.5)+2 \\ & =-0.7071+2 \\ & =1.2929 \mathrm{~m} \end{aligned} $$
(c)(i)
Diberi satu kitaran lengkap akan berlaku setiap 2 jam
$$ \begin{aligned} & b=\frac{360}{2}=180 \\ & y=\sin 180 x+2 \end{aligned} $$
$$ \begin{aligned} & y=\sin 180(0)+2 \\ & y=0+2=2 \end{aligned} $$
$$ \begin{aligned} & y=\sin 180(0.5)+2 \\ & y=1+2=3 \end{aligned} $$
$$ \begin{aligned} & y=\sin 180(1)+2 \\ & y=0+2=2 \end{aligned} $$
$$ \begin{aligned} & y=\sin 180(1.5)+2 \\ & y=-1+2=1 \end{aligned} $$


(c)(ii) Rajah 8 menunjukkan bilangan melepaskan air dalam masa 4 jam ialah satu kali manakala Rajah (c)(i) menunjukkan bilangan melepaskan air dalam masa 4 jam ialah dua kali.