Soalan 12:

Persatuan Sejarah telah memperkenalkan permainan tradisional kepada 40 orang ahlinya. Sebanyak 17 orang bermain ceper, 25 orang bermain batu seremban, 18 orang bermain congkak, 8 orang bermain ceper dan batu seremban, 12 orang bermain batu seremban dan congkak, dan 3 orang bermain ceper, congkak dan batu seremban.
Jika bilangan ahli yang hanya bermain batu seremban ialah dua kali bilangan ahli yang hanya bermain congkak, hitung bilangan ahli
(a) yang bermain batu seremban sahaja,
(b) yang bermain kedua-dua permainan ceper dan congkak,
(c) yang bermain ceper sahaja,
(d) yang tidak melibatkan diri dalam permainan tradisional.
Penyelesaian:
$$ \begin{aligned} & \text { Katakan } C=\text { Ceper } \\ & B=\text { Batu seremban } \\ & K=\text { Congkak } \end{aligned} $$
$$ \begin{aligned} & n(\xi)=40 \\ & n(C)=17 \\ & n(B)=25 \\ & n(K)=18 \\ & n(C \cap B)=8 \\ & n(B \cap K)=12 \\ & n(C \cap K \cap B)=3 \end{aligned} $$
$$ \text { Diberi } n \text { ( } B \text { sahaja) : } 2 \times n \text { ( } K \text { sahaja) } $$
$$ \text { Katakan } n(K \text { sahaja })=x $$
$$ \text { Maka, } n(B \text { sahaja })=2 x $$
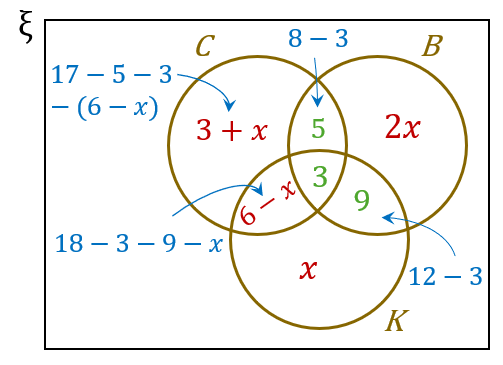
(a)
$$ \begin{aligned} n(B) & =25 \\ 5+3+9+2 x & =25 \\ 17+2 x & =25 \\ 2 x & =8 \\ x & =4 \\ n(B \text { sahaja }) & =2 x \\ & =2(4) \\ & =8 \end{aligned} $$
(b)
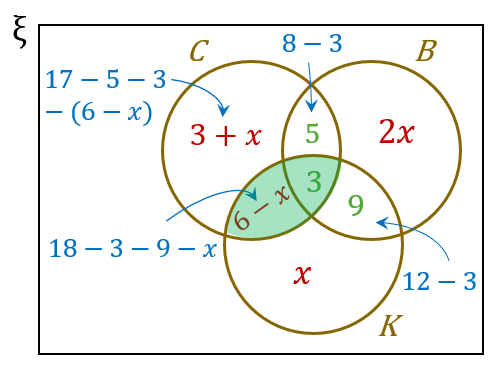
$$ \begin{aligned} n(C \cap K) & =6-x+3 \\ & =6-4+3 \\ & =5 \end{aligned} $$
(c)
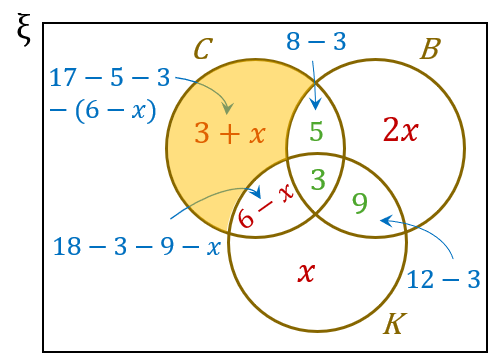
$$ \begin{aligned} n(C \text { sahaja }) & =3+x \\ & =3+4 \\ & =7 \end{aligned} $$
(d)
Katakan y = bilangan ahli yang tidak melibatkan diri dalam permainan tradisional
$$ \begin{aligned} n(\xi) & =40 \\ 3+x+6-x+5+3+9+2 x+x+y & =40 \\ 26+3 x+y & =40 \\ 26+3(4)+y & =40 \\ 38+y & =40 \\ y & =2 \end{aligned} $$

Persatuan Sejarah telah memperkenalkan permainan tradisional kepada 40 orang ahlinya. Sebanyak 17 orang bermain ceper, 25 orang bermain batu seremban, 18 orang bermain congkak, 8 orang bermain ceper dan batu seremban, 12 orang bermain batu seremban dan congkak, dan 3 orang bermain ceper, congkak dan batu seremban.
Jika bilangan ahli yang hanya bermain batu seremban ialah dua kali bilangan ahli yang hanya bermain congkak, hitung bilangan ahli
(a) yang bermain batu seremban sahaja,
(b) yang bermain kedua-dua permainan ceper dan congkak,
(c) yang bermain ceper sahaja,
(d) yang tidak melibatkan diri dalam permainan tradisional.
Penyelesaian:
$$ \begin{aligned} & \text { Katakan } C=\text { Ceper } \\ & B=\text { Batu seremban } \\ & K=\text { Congkak } \end{aligned} $$
$$ \begin{aligned} & n(\xi)=40 \\ & n(C)=17 \\ & n(B)=25 \\ & n(K)=18 \\ & n(C \cap B)=8 \\ & n(B \cap K)=12 \\ & n(C \cap K \cap B)=3 \end{aligned} $$
$$ \text { Diberi } n \text { ( } B \text { sahaja) : } 2 \times n \text { ( } K \text { sahaja) } $$
$$ \text { Katakan } n(K \text { sahaja })=x $$
$$ \text { Maka, } n(B \text { sahaja })=2 x $$

(a)
$$ \begin{aligned} n(B) & =25 \\ 5+3+9+2 x & =25 \\ 17+2 x & =25 \\ 2 x & =8 \\ x & =4 \\ n(B \text { sahaja }) & =2 x \\ & =2(4) \\ & =8 \end{aligned} $$
(b)

$$ \begin{aligned} n(C \cap K) & =6-x+3 \\ & =6-4+3 \\ & =5 \end{aligned} $$
(c)

$$ \begin{aligned} n(C \text { sahaja }) & =3+x \\ & =3+4 \\ & =7 \end{aligned} $$
(d)
Katakan y = bilangan ahli yang tidak melibatkan diri dalam permainan tradisional
$$ \begin{aligned} n(\xi) & =40 \\ 3+x+6-x+5+3+9+2 x+x+y & =40 \\ 26+3 x+y & =40 \\ 26+3(4)+y & =40 \\ 38+y & =40 \\ y & =2 \end{aligned} $$
Soalan 13:
Kajian terhadap 80 orang murid tentang penggunaan jenis pengangkutan ketika balik ke kampung menunjukkan sebanyak 25 orang murid menaiki kereta api dan 48 orang murid menaiki kereta api atau kereta. Jika 7 orang murid menaiki kereta api dan kereta, 5 orang murid menaiki bas dan kereta api serta 2 orang murid menggunakan ketiga-tiga pengangkutan tersebut, berapakah bilangan murid yang menaiki bas atau kereta api sahaja?
Penyelesaian:
$$ \begin{aligned} & \text { Katakan } A=\text { Kereta api } \\ & K=\text { Kereta } \\ & B=\text { Bas } \end{aligned} $$
$$ \begin{aligned} & n(\xi)=80 \\ & n(A)=25 \\ & n(A \cup K)=48 \\ & n(A \cap K)=7 \\ & n(B \cap A)=5 \\ & n(A \cap K \cap B)=2 \end{aligned} $$
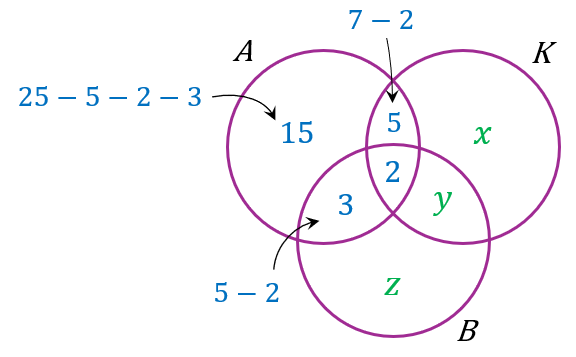
(A ∪ K) = 48
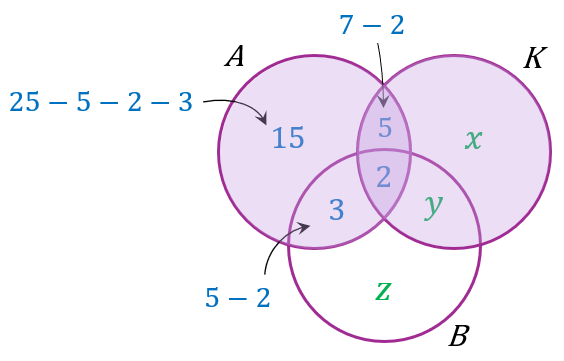
$$ \begin{array}{r} n(A \cup K)=48 \\ 15+5+3+2+x+y=48 \\ 25+x+y=48 \\ x+y=23 \ldots (1) \end{array} $$
n(ξ) = 80
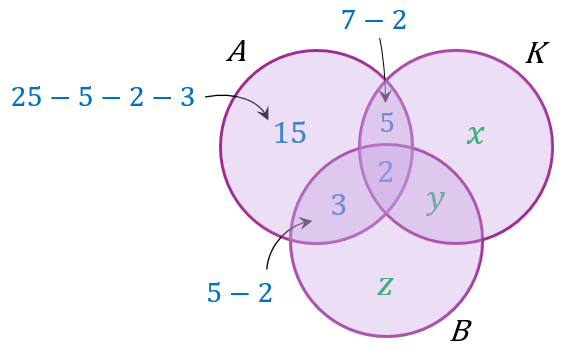
$$ \begin{aligned} 15+5+3+2+x+y+z & =80 \\ 25+x+y+z & =80 \\ x+y+z & =55 \ldots (2) \end{aligned} $$
$$ \begin{aligned} &\text { Gantikan (1) ke dalam (2): }\\ &\begin{aligned} (x+y)+z & =55 \\ 23+z & =55 \\ z & =32 \end{aligned} \end{aligned} $$
(B ∪ A sahaja)
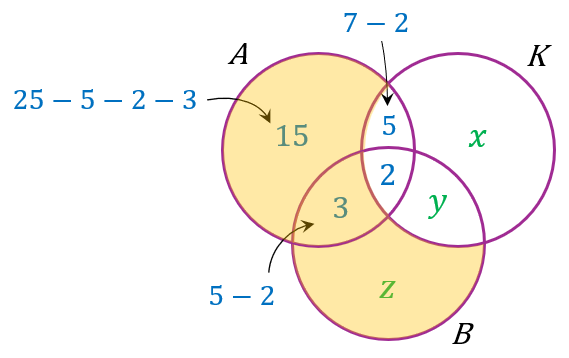
$$ \begin{aligned} n(B \cup A \text { sahaja }) & =15+3+z \\ & =18+32 \\ & =50 \end{aligned} $$
Kajian terhadap 80 orang murid tentang penggunaan jenis pengangkutan ketika balik ke kampung menunjukkan sebanyak 25 orang murid menaiki kereta api dan 48 orang murid menaiki kereta api atau kereta. Jika 7 orang murid menaiki kereta api dan kereta, 5 orang murid menaiki bas dan kereta api serta 2 orang murid menggunakan ketiga-tiga pengangkutan tersebut, berapakah bilangan murid yang menaiki bas atau kereta api sahaja?
Penyelesaian:
$$ \begin{aligned} & \text { Katakan } A=\text { Kereta api } \\ & K=\text { Kereta } \\ & B=\text { Bas } \end{aligned} $$
$$ \begin{aligned} & n(\xi)=80 \\ & n(A)=25 \\ & n(A \cup K)=48 \\ & n(A \cap K)=7 \\ & n(B \cap A)=5 \\ & n(A \cap K \cap B)=2 \end{aligned} $$

(A ∪ K) = 48
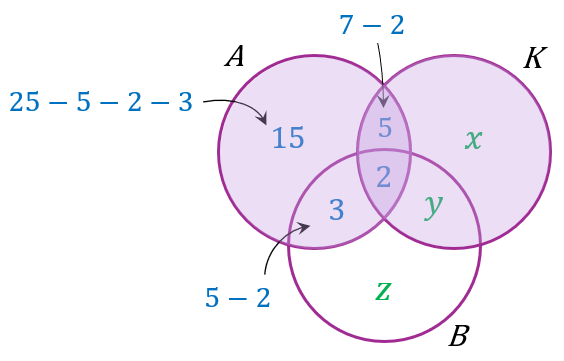
$$ \begin{array}{r} n(A \cup K)=48 \\ 15+5+3+2+x+y=48 \\ 25+x+y=48 \\ x+y=23 \ldots (1) \end{array} $$
n(ξ) = 80
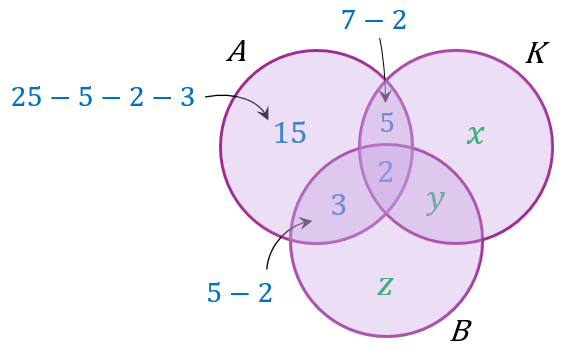
$$ \begin{aligned} 15+5+3+2+x+y+z & =80 \\ 25+x+y+z & =80 \\ x+y+z & =55 \ldots (2) \end{aligned} $$
$$ \begin{aligned} &\text { Gantikan (1) ke dalam (2): }\\ &\begin{aligned} (x+y)+z & =55 \\ 23+z & =55 \\ z & =32 \end{aligned} \end{aligned} $$
(B ∪ A sahaja)

$$ \begin{aligned} n(B \cup A \text { sahaja }) & =15+3+z \\ & =18+32 \\ & =50 \end{aligned} $$