Soalan 1:
Diberi set semesta, ξ = {2, 3, 5, 6}, set P = {3, 5}, set Q = {2, 3, 5} dan set R = {3, 6}.
Senaraikan semua unsur bagi set yang berikut.
(a) P ∩ Q
(b) P ∩ R
(c) P ∩ Q ∩ R
(d) (P ∩ Q ∩ R)’
Penyelesaian:
Persilangan set wujud apabila terdapat lebih daripada satu set. Persilangan set P dan set Q ditulis menggunakan simbol ∩. P ∩ Q ialah set yang mengandungi unsur-unsur sepunya bagi kedua-dua set P dan set Q.
$$ \begin{aligned} & \xi=\{2,3,5,6\} \\ & P=\{3,5\} \\ & Q=\{2,3,5\} \\ & R=\{3,6\} \end{aligned} $$
$$ \text { (a) } P \cap Q=\{3,5\} $$
$$ \text { (b) } P \cap R=\{3\} $$
$$ \text { (c) } P \cap Q \cap R=\{3\} $$
$$ \text { (d) }(P \cap Q \cap R)^{\prime}=\{2,5,6\} $$
Diberi set semesta, ξ = {2, 3, 5, 6}, set P = {3, 5}, set Q = {2, 3, 5} dan set R = {3, 6}.
Senaraikan semua unsur bagi set yang berikut.
(a) P ∩ Q
(b) P ∩ R
(c) P ∩ Q ∩ R
(d) (P ∩ Q ∩ R)’
Penyelesaian:
Persilangan set wujud apabila terdapat lebih daripada satu set. Persilangan set P dan set Q ditulis menggunakan simbol ∩. P ∩ Q ialah set yang mengandungi unsur-unsur sepunya bagi kedua-dua set P dan set Q.
$$ \begin{aligned} & \xi=\{2,3,5,6\} \\ & P=\{3,5\} \\ & Q=\{2,3,5\} \\ & R=\{3,6\} \end{aligned} $$
$$ \text { (a) } P \cap Q=\{3,5\} $$
$$ \text { (b) } P \cap R=\{3\} $$
$$ \text { (c) } P \cap Q \cap R=\{3\} $$
$$ \text { (d) }(P \cap Q \cap R)^{\prime}=\{2,5,6\} $$
Soalan 2:
Diberi set M = {b, a, i, k}, set N = {b, u, d, i} dan set P = {b, e, r, a, n, i}. Senaraikan semua unsur bagi set yang berikut.
(a) M ∪ N
(b) M ∪ P
(c) M ∪ N ∪ P
Penyelesaian:
Kesatuan set P dan set Q ditulis menggunakan simbol ∪. P ∪ Q mewakili semua unsur dalam set P atau set Q atau kedua-dua set P dan set Q.
$$ \text { (a) } M \cup N=\{\mathrm{a}, \mathrm{~b}, \mathrm{~d}, \mathrm{i}, \mathrm{k}, \mathrm{u}\} $$
$$ \text { (b) } M \cup P=\{\mathrm{a}, \mathrm{~b}, \mathrm{e}, \mathrm{i}, \mathrm{k}, \mathrm{n}, \mathrm{r}\} $$
$$ \text { (c) } M \cup N \cup P=\{\mathrm{a}, \mathrm{~b}, \mathrm{~d}, \mathrm{e}, \mathrm{i}, \mathrm{k}, \mathrm{n}, \mathrm{r}, \mathrm{u}\} $$
Diberi set M = {b, a, i, k}, set N = {b, u, d, i} dan set P = {b, e, r, a, n, i}. Senaraikan semua unsur bagi set yang berikut.
(a) M ∪ N
(b) M ∪ P
(c) M ∪ N ∪ P
Penyelesaian:
Kesatuan set P dan set Q ditulis menggunakan simbol ∪. P ∪ Q mewakili semua unsur dalam set P atau set Q atau kedua-dua set P dan set Q.
$$ \text { (a) } M \cup N=\{\mathrm{a}, \mathrm{~b}, \mathrm{~d}, \mathrm{i}, \mathrm{k}, \mathrm{u}\} $$
$$ \text { (b) } M \cup P=\{\mathrm{a}, \mathrm{~b}, \mathrm{e}, \mathrm{i}, \mathrm{k}, \mathrm{n}, \mathrm{r}\} $$
$$ \text { (c) } M \cup N \cup P=\{\mathrm{a}, \mathrm{~b}, \mathrm{~d}, \mathrm{e}, \mathrm{i}, \mathrm{k}, \mathrm{n}, \mathrm{r}, \mathrm{u}\} $$
Soalan 3:
Lorekkan kawasan yang mewakili set yang diberikan, dengan keadaan set semesta, ξ = P ∪ Q ∪ R
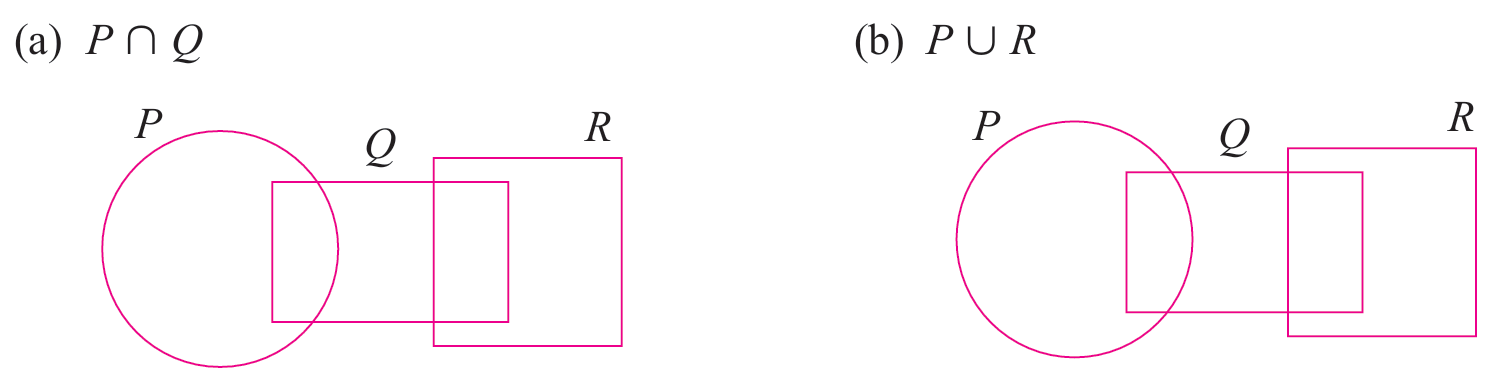
Penyelesaian:
(a) P ∩ Q
Set P ∩ Q adalah kawasan persilangan antara set P dan set Q.
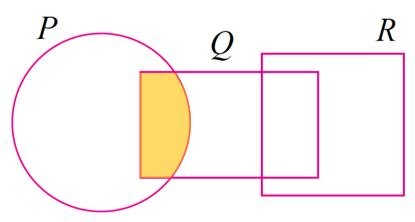
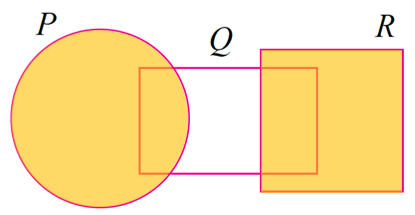
(b) P ∪ R
Set P ∪ R adalah semua kawasan yang meliputi kedua-dua set P dan set R.
Lorekkan kawasan yang mewakili set yang diberikan, dengan keadaan set semesta, ξ = P ∪ Q ∪ R

Penyelesaian:
(a) P ∩ Q
Set P ∩ Q adalah kawasan persilangan antara set P dan set Q.
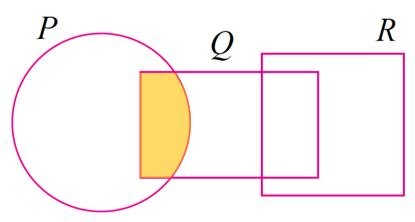
(b) P ∪ R
Set P ∪ R adalah semua kawasan yang meliputi kedua-dua set P dan set R.

Soalan 4:
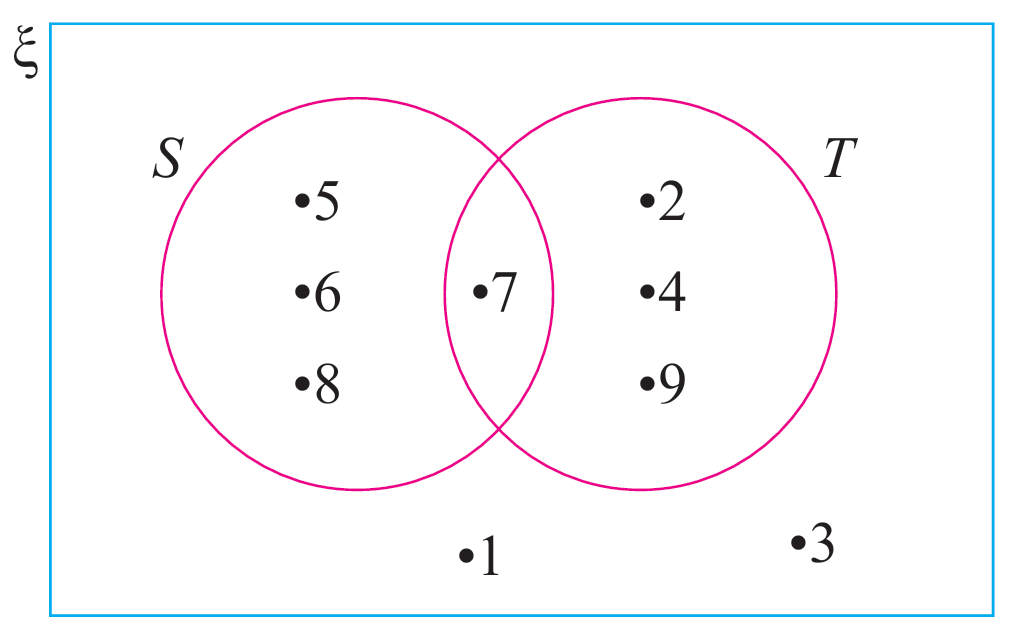
Gambar rajah Venn menunjukkan set semesta ξ, set S dan set T.
Senaraikan semua unsur bagi set yang berikut.
(a) T ‘
(b) S ∪ T
(c) S ‘ ∩ T
(d) (S ∩ T)’
Penyelesaian:
Pelengkap bagi kesatuan set ditulis dengan menggunakan (A ∪ B)’, dibaca sebagai “pelengkap bagi kesatuan set A atau set B ”.
Pelengkap bagi kesatuan set A atau set B bermaksud semua unsur yang bukan dalam set A atau set B.
$$ \text { (a) } T^{\prime}=\{1,3,5,6,8\} $$
$$ \text { (b) }(S \cup T)=\{2,4,5,6,7,8,9\} $$
$$ \text { (c) }\left(S^{\prime} \cap T\right)=\{2,4,9\} $$
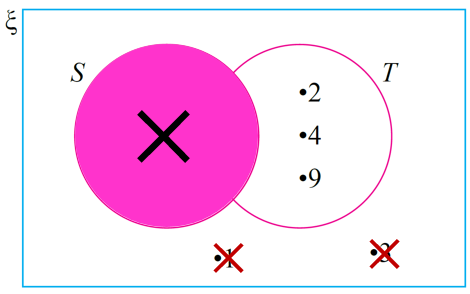
$$ \text { (d) }(S \cap T)^{\prime}=\{1,2,3,4,5,6,8,9\} $$
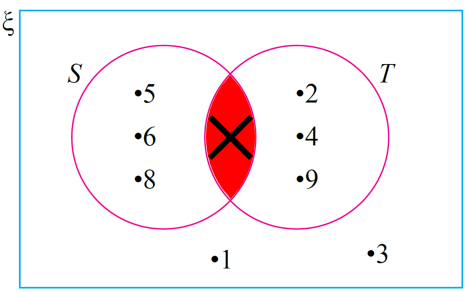

Gambar rajah Venn menunjukkan set semesta ξ, set S dan set T.
Senaraikan semua unsur bagi set yang berikut.
(a) T ‘
(b) S ∪ T
(c) S ‘ ∩ T
(d) (S ∩ T)’
Penyelesaian:
Pelengkap bagi kesatuan set ditulis dengan menggunakan (A ∪ B)’, dibaca sebagai “pelengkap bagi kesatuan set A atau set B ”.
Pelengkap bagi kesatuan set A atau set B bermaksud semua unsur yang bukan dalam set A atau set B.
$$ \text { (a) } T^{\prime}=\{1,3,5,6,8\} $$
$$ \text { (b) }(S \cup T)=\{2,4,5,6,7,8,9\} $$
$$ \text { (c) }\left(S^{\prime} \cap T\right)=\{2,4,9\} $$

$$ \text { (d) }(S \cap T)^{\prime}=\{1,2,3,4,5,6,8,9\} $$

Soalan 5:
Gambar rajah Venn menunjukkan unsur-unsur set A, set B dan set C. Jika set semesta, ξ = A ∪ B ∪ C, senaraikan unsur A’.
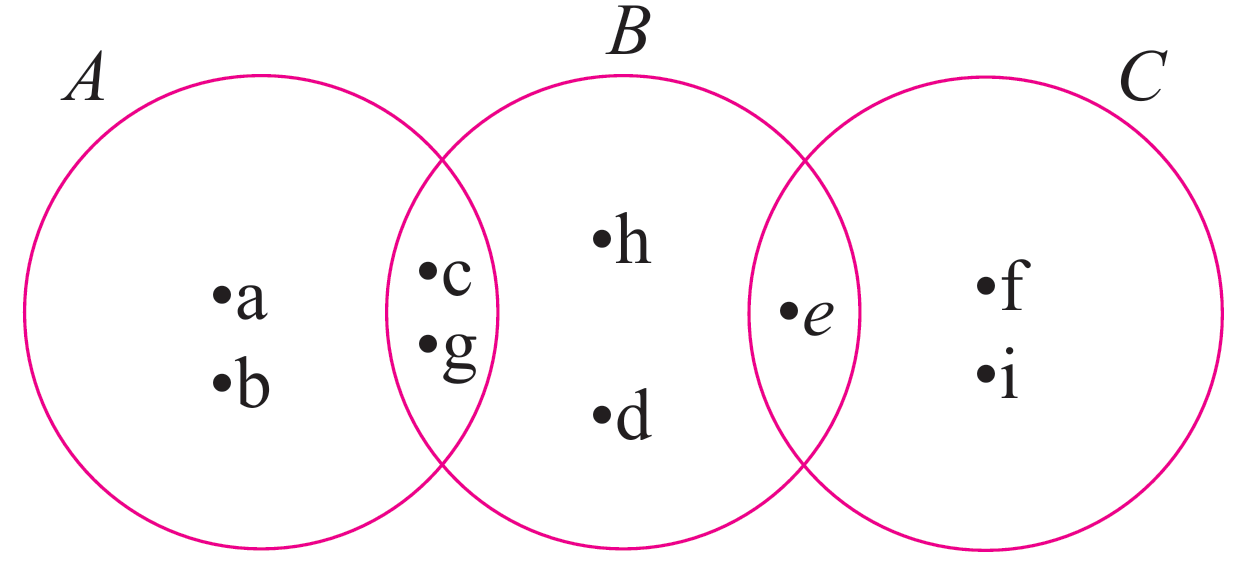
Penyelesaian:
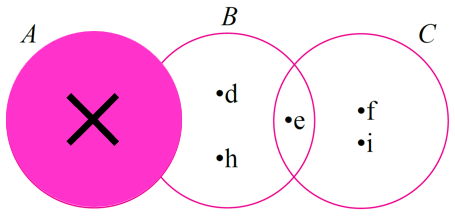
$$ \begin{aligned} & \xi=A \cup B \cup C \\ & A^{\prime}=\{\mathrm{d}, \mathrm{e}, \mathrm{f}, \mathrm{~h}, \mathrm{i}\} \end{aligned} $$
Gambar rajah Venn menunjukkan unsur-unsur set A, set B dan set C. Jika set semesta, ξ = A ∪ B ∪ C, senaraikan unsur A’.

Penyelesaian:

$$ \begin{aligned} & \xi=A \cup B \cup C \\ & A^{\prime}=\{\mathrm{d}, \mathrm{e}, \mathrm{f}, \mathrm{~h}, \mathrm{i}\} \end{aligned} $$