Soalan 1:
Diberi ξ = {x : x ialah integer, 10 ≤ x ≤ 20}, set L = {x : x ialah gandaan 2}, set M = {13, 16, 19} dan set N = {x : x ialah gandaan 5}, senaraikan semua unsur bagi set yang berikut.
(a) L’ ∩ ( M ∪ N)
(b) (M ∪ N )’ ∩ L
Penyelesaian:
$$ \begin{aligned} & \xi=\{x: x \text { ialah integer, } 10 \leq x \leq 20\} \\ & \xi=\{10,11,12,13,14,15,16,17,18,19,20\} \end{aligned} $$
$$ \begin{aligned} & L=\{x: x \text { ialah gandaan } 2\} \\ & L=\{10,12,14,16,18,20\} \end{aligned} $$
$$ \begin{aligned} & M=\{13,16,19\} \\ & N=\{x: x \text { ialah gandaan } 5\} \\ & N=\{10,15,20\} \end{aligned} $$
(a)
$$ \begin{aligned} & L^{\prime}=\{11,13,15,17,19\} \\ & M \cup N=\{10,13,15,16,19,20\} \\ & L^{\prime} \cap(M \cup N)=\{13,15,19\} \end{aligned} $$
(b)
$$ \begin{aligned} & (M \cup N)^{\prime}=\{11,12,14,17,18\} \\ & (M \cup N)^{\prime} \cap L=\{12,14,18\} \end{aligned} $$
Diberi ξ = {x : x ialah integer, 10 ≤ x ≤ 20}, set L = {x : x ialah gandaan 2}, set M = {13, 16, 19} dan set N = {x : x ialah gandaan 5}, senaraikan semua unsur bagi set yang berikut.
(a) L’ ∩ ( M ∪ N)
(b) (M ∪ N )’ ∩ L
Penyelesaian:
$$ \begin{aligned} & \xi=\{x: x \text { ialah integer, } 10 \leq x \leq 20\} \\ & \xi=\{10,11,12,13,14,15,16,17,18,19,20\} \end{aligned} $$
$$ \begin{aligned} & L=\{x: x \text { ialah gandaan } 2\} \\ & L=\{10,12,14,16,18,20\} \end{aligned} $$
$$ \begin{aligned} & M=\{13,16,19\} \\ & N=\{x: x \text { ialah gandaan } 5\} \\ & N=\{10,15,20\} \end{aligned} $$
(a)
$$ \begin{aligned} & L^{\prime}=\{11,13,15,17,19\} \\ & M \cup N=\{10,13,15,16,19,20\} \\ & L^{\prime} \cap(M \cup N)=\{13,15,19\} \end{aligned} $$
(b)
$$ \begin{aligned} & (M \cup N)^{\prime}=\{11,12,14,17,18\} \\ & (M \cup N)^{\prime} \cap L=\{12,14,18\} \end{aligned} $$
Soalan 2:
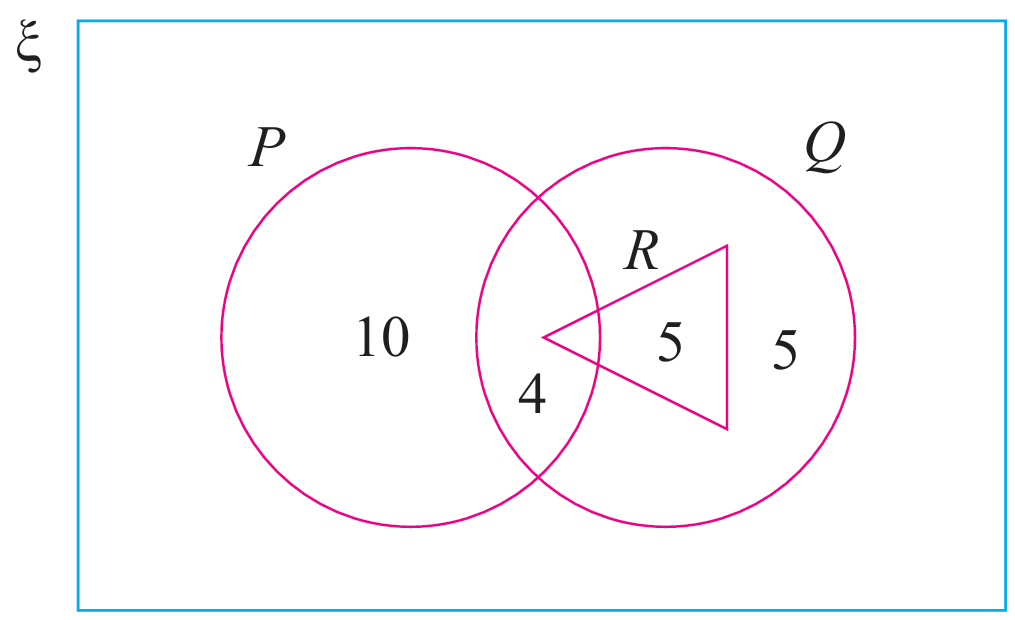
Gambar rajah Venn menunjukkan bilangan unsur dalam set P, set Q dan set R yang belum lengkap. Diberi bahawa n( P ∩ Q ) = n( P ∪ Q )’ dan n(ξ) = 50. Tentukan n(P).
Penyelesaian:
$$ \begin{aligned} n(P \cap Q) & =n(P \cup Q)^{\prime} \\ x+4 & =y \\ y & =x+4 \ldots(1) \end{aligned} $$
$$ \begin{aligned} n(\xi) & =50 \\ 10+4+5+5+x+y & =50 \\ x+y+24 & =50 \\ x+y & =26 \ldots(2) \end{aligned} $$
$$ \begin{aligned} &\text { Gantikan (1) ke dalam (2), }\\ &\begin{aligned} x+(x+4) & =26 \\ 2 x & =22 \\ x & =11 \end{aligned} \end{aligned} $$
$$ \begin{aligned} n(P) & =10+4+x \\ & =10+4+11 \\ & =25 \end{aligned} $$

Gambar rajah Venn menunjukkan bilangan unsur dalam set P, set Q dan set R yang belum lengkap. Diberi bahawa n( P ∩ Q ) = n( P ∪ Q )’ dan n(ξ) = 50. Tentukan n(P).
Penyelesaian:
$$ \begin{aligned} n(P \cap Q) & =n(P \cup Q)^{\prime} \\ x+4 & =y \\ y & =x+4 \ldots(1) \end{aligned} $$
$$ \begin{aligned} n(\xi) & =50 \\ 10+4+5+5+x+y & =50 \\ x+y+24 & =50 \\ x+y & =26 \ldots(2) \end{aligned} $$
$$ \begin{aligned} &\text { Gantikan (1) ke dalam (2), }\\ &\begin{aligned} x+(x+4) & =26 \\ 2 x & =22 \\ x & =11 \end{aligned} \end{aligned} $$
$$ \begin{aligned} n(P) & =10+4+x \\ & =10+4+11 \\ & =25 \end{aligned} $$
Soalan 3:
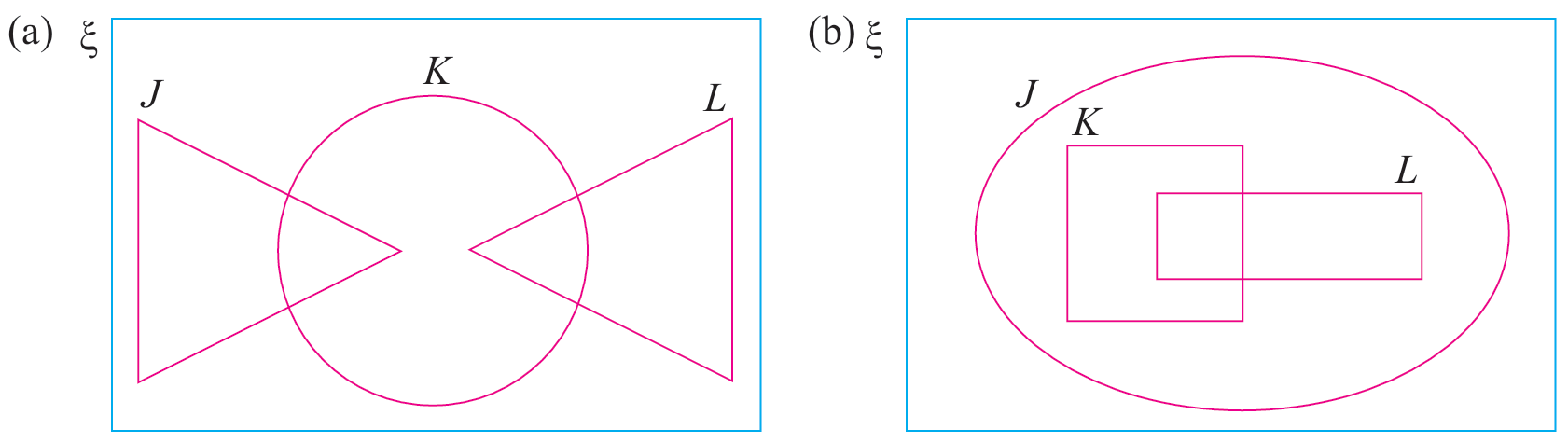
Lorekkan kawasan yang mewakili (J ∩ K)’ ∩ (K ∪ L).
Penyelesaian:
(a) (J ∩ K)′ ∩ (K ∪ L)
Langkah 1:
Lorekkan kawasan bagi set (J ∩ K)′
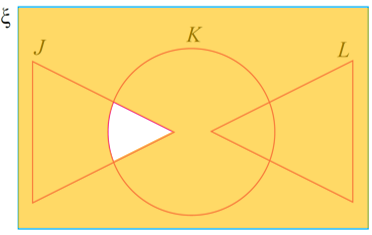
Langkah 2:
Lorekkan kawasan bagi set (K ∪ L)
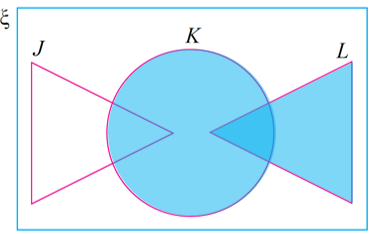
Langkah 3:
Set (J ∩ K)′ ∩ (K ∪ L) ialah kawasan yang sama meliputi kedua-dua set (J ∩ K)′ dan (K ∪ L).
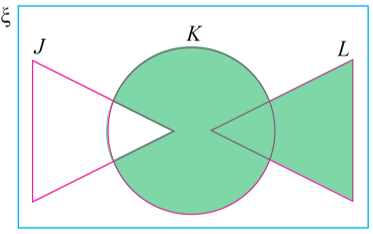
(b) (J ∩ K)′ ∩ (K ∪ L)
Langkah 1:
Lorekkan kawasan bagi set (J ∩ K)′
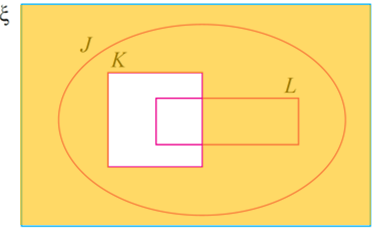
Langkah 2:
Lorekkan kawasan bagi set (K ∪ L)
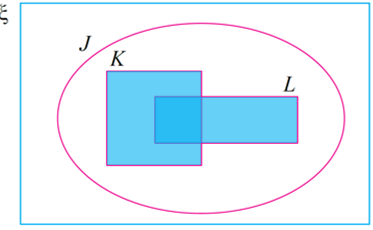
Langkah 3:
Set (J ∩ K)′ ∩ (K ∪ L) ialah kawasan yang sama meliputi kedua-dua set (J ∩ K)′ dan (K ∪ L).
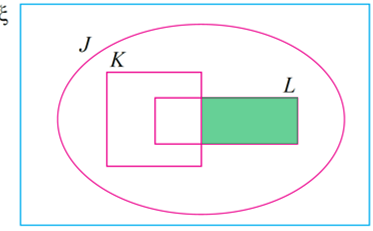
Lorekkan kawasan yang mewakili (J ∩ K)’ ∩ (K ∪ L).

Penyelesaian:
(a) (J ∩ K)′ ∩ (K ∪ L)
Langkah 1:
Lorekkan kawasan bagi set (J ∩ K)′

Langkah 2:
Lorekkan kawasan bagi set (K ∪ L)

Langkah 3:
Set (J ∩ K)′ ∩ (K ∪ L) ialah kawasan yang sama meliputi kedua-dua set (J ∩ K)′ dan (K ∪ L).

(b) (J ∩ K)′ ∩ (K ∪ L)
Langkah 1:
Lorekkan kawasan bagi set (J ∩ K)′

Langkah 2:
Lorekkan kawasan bagi set (K ∪ L)

Langkah 3:
Set (J ∩ K)′ ∩ (K ∪ L) ialah kawasan yang sama meliputi kedua-dua set (J ∩ K)′ dan (K ∪ L).

Soalan 4:
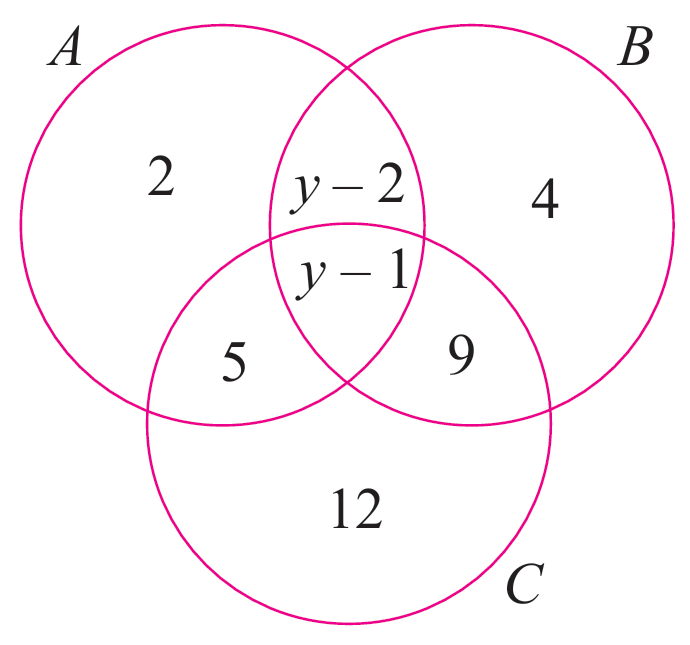
Gambar rajah Venn menunjukkan set semesta.
ξ = A ∪ B ∪ C dan n(B’) = n(B ∩ C)
Tentukan,
(a) nilai y
(b) n(A ∪ B ∪ C)
Penyelesaian:
(a)
$$ \begin{aligned} n(B)^{\prime} & =n(B \cap C) \\ 2+5+12 & =y-1+9 \\ 19 & =y+8 \\ y & =11 \end{aligned} $$
(b)
$$ \begin{aligned} n(A \cup B \cup C) & =2+5+12+9+4+(y-2)+(y-1) \\ & =32+(11-2)+(11-1) \\ & =32+9+10 \\ & =51 \end{aligned} $$

Gambar rajah Venn menunjukkan set semesta.
ξ = A ∪ B ∪ C dan n(B’) = n(B ∩ C)
Tentukan,
(a) nilai y
(b) n(A ∪ B ∪ C)
Penyelesaian:
(a)
$$ \begin{aligned} n(B)^{\prime} & =n(B \cap C) \\ 2+5+12 & =y-1+9 \\ 19 & =y+8 \\ y & =11 \end{aligned} $$
(b)
$$ \begin{aligned} n(A \cup B \cup C) & =2+5+12+9+4+(y-2)+(y-1) \\ & =32+(11-2)+(11-1) \\ & =32+9+10 \\ & =51 \end{aligned} $$