Soalan 1:
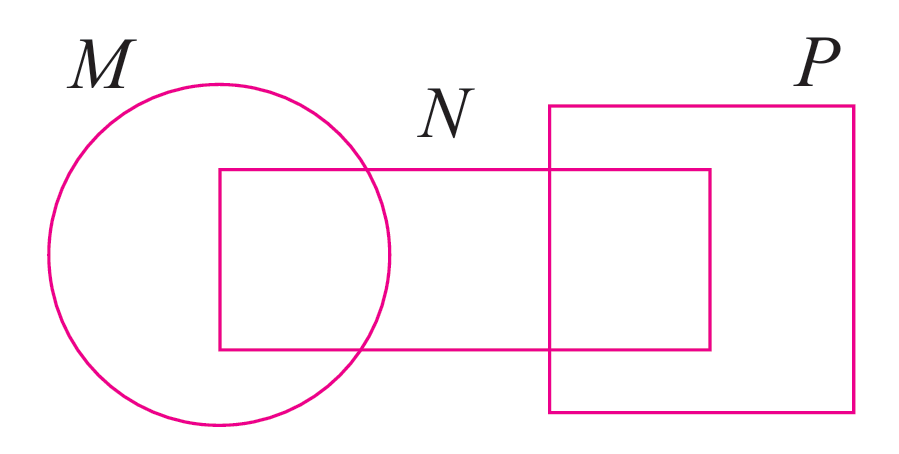
Gambar rajah Venn menunjukkan set M, set N dan set P dengan keadaan set semesta, ξ = M ∪ N ∪ P. Lorekkan set (M ∪ P) ∩ N.
Penyelesaian:
Gabungan operasi set melibatkan kedua-dua persilangan set (∩) dan kesatuan set (∪) pada masa yang sama. Gabungan operasi set perlu diselesaikan dari kiri ke kanan, namun jika terdapat operasi dalam kurungan, operasi dalam kurungan mesti diselesaikan dahulu.
Langkah 1:
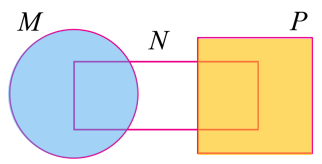
Lorekkan kawasan bagi set (M ∪ P)
Langkah 2:
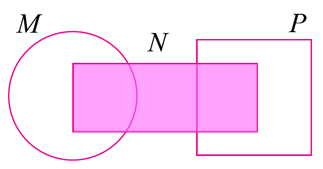
Lorekkan kawasan bagi set N
Langkah 3:
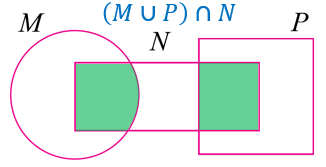
Set (M ∪ P) ∩ N ialah kawasan yang sama meliputi kedua-dua set (M ∪ P) dan N

Gambar rajah Venn menunjukkan set M, set N dan set P dengan keadaan set semesta, ξ = M ∪ N ∪ P. Lorekkan set (M ∪ P) ∩ N.
Penyelesaian:
Gabungan operasi set melibatkan kedua-dua persilangan set (∩) dan kesatuan set (∪) pada masa yang sama. Gabungan operasi set perlu diselesaikan dari kiri ke kanan, namun jika terdapat operasi dalam kurungan, operasi dalam kurungan mesti diselesaikan dahulu.
Langkah 1:
Lorekkan kawasan bagi set (M ∪ P)

Langkah 2:
Lorekkan kawasan bagi set N

Langkah 3:
Set (M ∪ P) ∩ N ialah kawasan yang sama meliputi kedua-dua set (M ∪ P) dan N

Soalan 2:
Diberi set semesta, ξ = {x : x ialah integer, 1 ≤ x ≤ 15}, set S = {x : x ialah nombor ganjil}, set R = {x : x ialah nombor perdana} dan set T = {1, 4, 7, 10, 13}. Senaraikan semua unsur bagi set (S ∪ T) ∩ R.
Penyelesaian:
$$ \begin{aligned} & \xi=\{x: x \text { ialah integer, } 1 \leq x \leq 15\} \\ & \xi=\{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15\} \end{aligned} $$
$$ \begin{aligned} & S=\{x: x \text { ialah nombor ganjil }\} \\ & S=\{1,3,5,7,9,11,13,15\} \end{aligned} $$
$$ \begin{aligned} & R=\{x: x \text { ialah nombor perdana }\} \\ & R=\{2,3,5,7,11,13\} \end{aligned} $$
$$ T=\{1,4,7,10,13\} $$
$$ S \cup T=\{1,3,4,5,7,9,10,11,13,15\} $$
$$ (S \cup T) \cap R=\{3,5,7,11,13\} $$
Diberi set semesta, ξ = {x : x ialah integer, 1 ≤ x ≤ 15}, set S = {x : x ialah nombor ganjil}, set R = {x : x ialah nombor perdana} dan set T = {1, 4, 7, 10, 13}. Senaraikan semua unsur bagi set (S ∪ T) ∩ R.
Penyelesaian:
$$ \begin{aligned} & \xi=\{x: x \text { ialah integer, } 1 \leq x \leq 15\} \\ & \xi=\{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15\} \end{aligned} $$
$$ \begin{aligned} & S=\{x: x \text { ialah nombor ganjil }\} \\ & S=\{1,3,5,7,9,11,13,15\} \end{aligned} $$
$$ \begin{aligned} & R=\{x: x \text { ialah nombor perdana }\} \\ & R=\{2,3,5,7,11,13\} \end{aligned} $$
$$ T=\{1,4,7,10,13\} $$
$$ S \cup T=\{1,3,4,5,7,9,10,11,13,15\} $$
$$ (S \cup T) \cap R=\{3,5,7,11,13\} $$
Soalan 3:
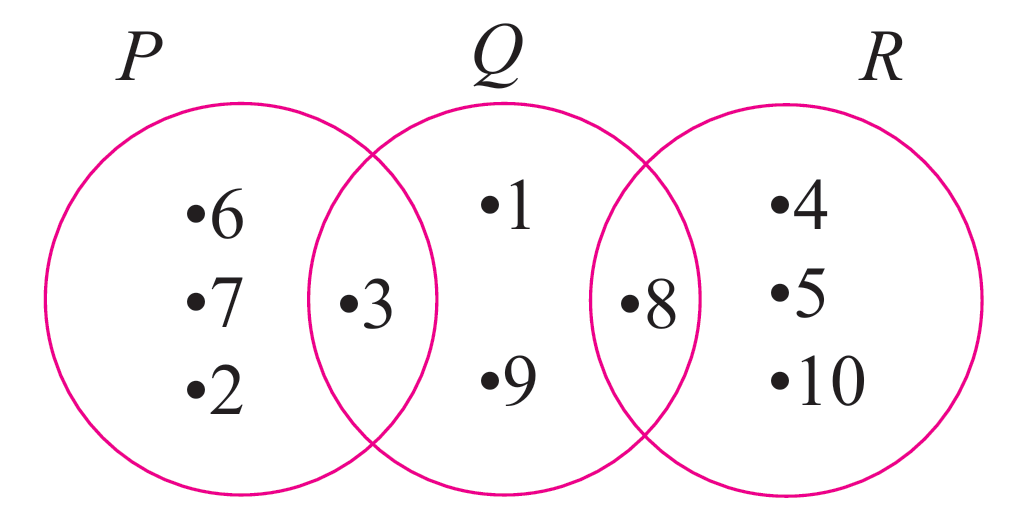
Gambar rajah Venn menunjukkan set P, set Q dan set R dengan keadaan set semesta, ξ = P ∪ Q ∪ R. Senaraikan semua unsur bagi set yang berikut.
(a) P ∩ (Q ∪ R)
(b) Q ∩ (P ∪ R)
(c) (Q ∩ R) ∪ P
Penyelesaian:
P = {2, 3, 6, 7}
Q = {1, 3, 8, 9}
R = {4, 5, 8, 10}
(a)
Langkah 1 : Senaraikan unsur bagi set (Q ∪ R)
(Q ∪ R) = {1, 3, 4, 5, 8, 9, 10}
Langkah 2 : Senaraikan unsur yang sama meliputi kedua-dua set (Q ∪ R) dan P.
P ∩ (Q ∪ R) = {3}
(b)
Langkah 1 : Senaraikan unsur bagi set (P ∪ R)
(P ∪ R) = {2, 3, 4, 5, 6, 7, 8, 10}
Langkah 2 : Senaraikan unsur yang sama meliputi kedua-dua set (P ∪ R) dan Q.
Q ∩ (P ∪ R) = {3, 8}
(c)
Langkah 1 : Senaraikan unsur yang sama meliputi kedua-dua set set Q dan R.
(Q ∩ R) = {8}
Langkah 2 : Senaraikan unsur bagi set (Q ∩ R) ∪ P
(Q ∩ R) ∪ P = {2, 3, 6, 7, 8}
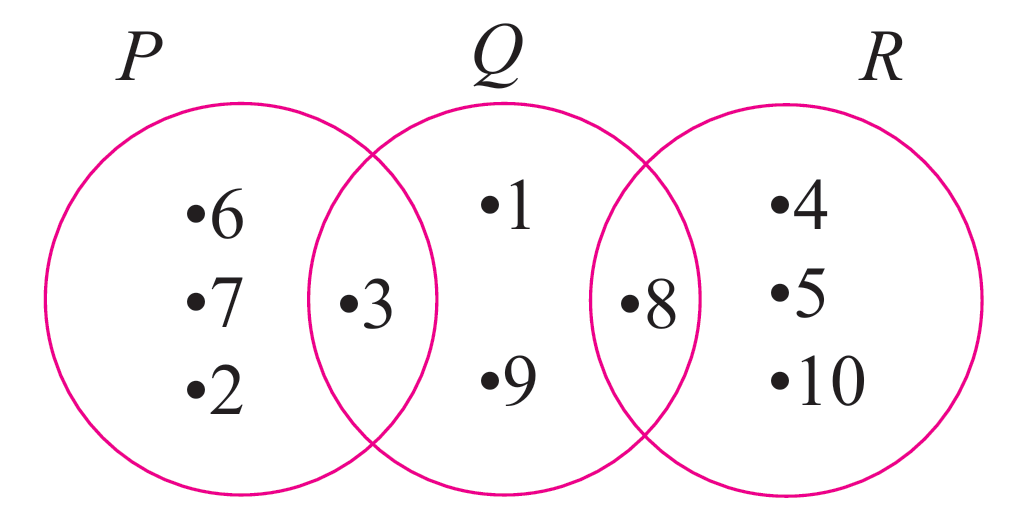
Gambar rajah Venn menunjukkan set P, set Q dan set R dengan keadaan set semesta, ξ = P ∪ Q ∪ R. Senaraikan semua unsur bagi set yang berikut.
(a) P ∩ (Q ∪ R)
(b) Q ∩ (P ∪ R)
(c) (Q ∩ R) ∪ P
Penyelesaian:
P = {2, 3, 6, 7}
Q = {1, 3, 8, 9}
R = {4, 5, 8, 10}
(a)
Langkah 1 : Senaraikan unsur bagi set (Q ∪ R)
(Q ∪ R) = {1, 3, 4, 5, 8, 9, 10}
Langkah 2 : Senaraikan unsur yang sama meliputi kedua-dua set (Q ∪ R) dan P.
P ∩ (Q ∪ R) = {3}
(b)
Langkah 1 : Senaraikan unsur bagi set (P ∪ R)
(P ∪ R) = {2, 3, 4, 5, 6, 7, 8, 10}
Langkah 2 : Senaraikan unsur yang sama meliputi kedua-dua set (P ∪ R) dan Q.
Q ∩ (P ∪ R) = {3, 8}
(c)
Langkah 1 : Senaraikan unsur yang sama meliputi kedua-dua set set Q dan R.
(Q ∩ R) = {8}
Langkah 2 : Senaraikan unsur bagi set (Q ∩ R) ∪ P
(Q ∩ R) ∪ P = {2, 3, 6, 7, 8}