Soalan 1:
Gambar rajah Venn menunjukkan unsur-unsur dalam set J, set K dan set L. Diberi ξ = J ∪ K ∪ L dan n(ξ) = 25, hitung nilai x.
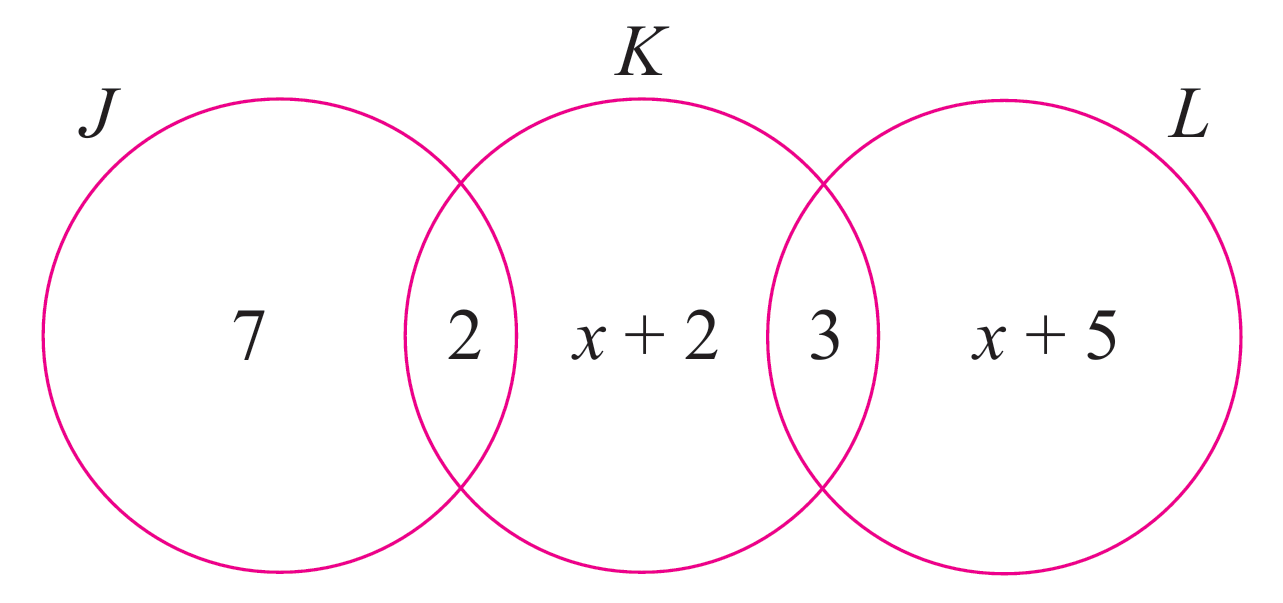
Penyelesaian:
$$ \begin{aligned} n(\xi) & =25 \\ 7+2+(x+2)+3+(x+5) & =25 \\ 2 x+19 & =25 \\ 2 x & =6 \\ x & =\frac{6}{2} \\ x & =3 \end{aligned} $$
Gambar rajah Venn menunjukkan unsur-unsur dalam set J, set K dan set L. Diberi ξ = J ∪ K ∪ L dan n(ξ) = 25, hitung nilai x.

Penyelesaian:
$$ \begin{aligned} n(\xi) & =25 \\ 7+2+(x+2)+3+(x+5) & =25 \\ 2 x+19 & =25 \\ 2 x & =6 \\ x & =\frac{6}{2} \\ x & =3 \end{aligned} $$
Soalan 2:
Diberi set B = {murid yang berasal dari Sabah} dan set T = {murid yang berasal dari Sarawak}. Jika sebuah kelas terdiri daripada 40 orang murid dan n(B ∪ T) = 32 , hitung bilangan murid yang tidak berasal dari Sabah dan Sarawak.
Penyelesaian:
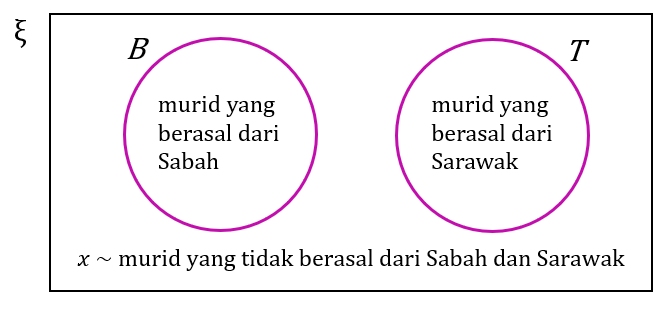 $$
\begin{aligned}
n(\xi) & =40 \\
n(B \cup T) & =32
\end{aligned}
$$
$$
\begin{aligned}
n(\xi) & =40 \\
n(B \cup T) & =32
\end{aligned}
$$
$$ \begin{aligned} &\text { Bilangan murid yang tidak berasal dari Sabah dan Sarawak, } x\\ &\begin{aligned} & =40-32 \\ & =8 \text { orang murid } \end{aligned} \end{aligned} $$
Diberi set B = {murid yang berasal dari Sabah} dan set T = {murid yang berasal dari Sarawak}. Jika sebuah kelas terdiri daripada 40 orang murid dan n(B ∪ T) = 32 , hitung bilangan murid yang tidak berasal dari Sabah dan Sarawak.
Penyelesaian:
 $$
\begin{aligned}
n(\xi) & =40 \\
n(B \cup T) & =32
\end{aligned}
$$
$$
\begin{aligned}
n(\xi) & =40 \\
n(B \cup T) & =32
\end{aligned}
$$$$ \begin{aligned} &\text { Bilangan murid yang tidak berasal dari Sabah dan Sarawak, } x\\ &\begin{aligned} & =40-32 \\ & =8 \text { orang murid } \end{aligned} \end{aligned} $$
Soalan 3:
Sebuah sekolah telah mengadakan sambutan Bulan Kemerdekaan dengan menganjurkan aktiviti drama, nyanyian lagu patriotik, dan kuiz Sejarah. Sebanyak 40 orang murid telah menyertai aktiviti tersebut. Diberi 1/2 daripada jumlah murid menyertai drama, 1/4 daripada jumlah murid menyertai nyanyian lagu patriotik, 6 orang murid menyertai drama dan kuiz Sejarah dan seorang murid menyertai ketiga-tiga aktiviti tersebut. Sekiranya tidak ada penyertaan murid dalam aktiviti drama dan lagu patriotik sahaja dan juga tidak ada penyertaan murid dalam aktiviti lagu patriotik dan kuiz Sejarah sahaja, berapakah bilangan murid yang menyertai kuiz Sejarah sahaja?
Penyelesaian:
Katakan D = drama
N = nyanyian
K = kuiz
$$ \begin{aligned} & n(\xi)=40 \\ & n(D)=\frac{1}{2} \times 40=20 \\ & n(N)=\frac{1}{4} \times 40=10 \\ & n(D \cap K)=6 \\ & n(D \cap N \cap K)=1 \\ & n(D \cap N)=0 \\ & n(N \cap K)=0 \end{aligned} $$
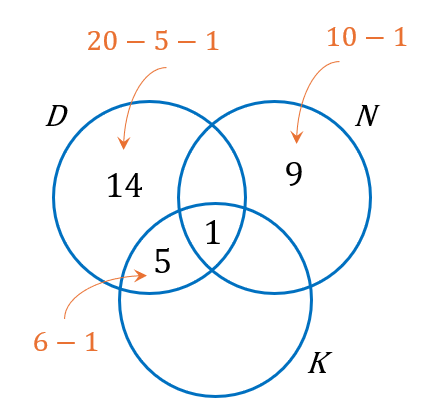 $$
\begin{aligned}
n(K \text { sahaja }) & =40-14-5-1-9 \\
& =11 \text { orang }
\end{aligned}
$$
$$
\begin{aligned}
n(K \text { sahaja }) & =40-14-5-1-9 \\
& =11 \text { orang }
\end{aligned}
$$
Sebuah sekolah telah mengadakan sambutan Bulan Kemerdekaan dengan menganjurkan aktiviti drama, nyanyian lagu patriotik, dan kuiz Sejarah. Sebanyak 40 orang murid telah menyertai aktiviti tersebut. Diberi 1/2 daripada jumlah murid menyertai drama, 1/4 daripada jumlah murid menyertai nyanyian lagu patriotik, 6 orang murid menyertai drama dan kuiz Sejarah dan seorang murid menyertai ketiga-tiga aktiviti tersebut. Sekiranya tidak ada penyertaan murid dalam aktiviti drama dan lagu patriotik sahaja dan juga tidak ada penyertaan murid dalam aktiviti lagu patriotik dan kuiz Sejarah sahaja, berapakah bilangan murid yang menyertai kuiz Sejarah sahaja?
Penyelesaian:
Katakan D = drama
N = nyanyian
K = kuiz
$$ \begin{aligned} & n(\xi)=40 \\ & n(D)=\frac{1}{2} \times 40=20 \\ & n(N)=\frac{1}{4} \times 40=10 \\ & n(D \cap K)=6 \\ & n(D \cap N \cap K)=1 \\ & n(D \cap N)=0 \\ & n(N \cap K)=0 \end{aligned} $$
 $$
\begin{aligned}
n(K \text { sahaja }) & =40-14-5-1-9 \\
& =11 \text { orang }
\end{aligned}
$$
$$
\begin{aligned}
n(K \text { sahaja }) & =40-14-5-1-9 \\
& =11 \text { orang }
\end{aligned}
$$Soalan 4:
Sebuah kedai buku membuat kajian terhadap 200 orang pelanggan berkaitan dengan pembelian buku fiksyen atau buku bukan fiksyen. Kajian menunjukkan 114 orang membeli buku bukan fiksyen, 52 orang membeli buku fiksyen dan 27 orang membeli kedua-dua buku fiksyen dan bukan fiksyen. Hitung,
(a) bilangan pelanggan yang membeli buku fiksyen sahaja.
(b) bilangan pelanggan yang membeli buku bukan fiksyen sahaja.
(c) bilangan pelanggan yang tidak membeli sebarang buku tersebut.
Penyelesaian:
Katakan F = fiksyen
B = bukan fiksyen
$$ \begin{aligned} & n(\xi)=200 \\ & n(B)=114 \\ & n(F)=52 \\ & n(B \cap F)=27 \end{aligned} $$
(a)
$$ \begin{aligned} n(F \text { sahaja }) & =52-27 \\ & =25 \end{aligned} $$
(b)
$$ \begin{aligned} n(B \text { sahaja }) & =114-27 \\ & =87 \end{aligned} $$
(c)
$$ \begin{aligned} n(F \cup B)^{\prime} & =200-25-27-87 \\ & =61 \end{aligned} $$
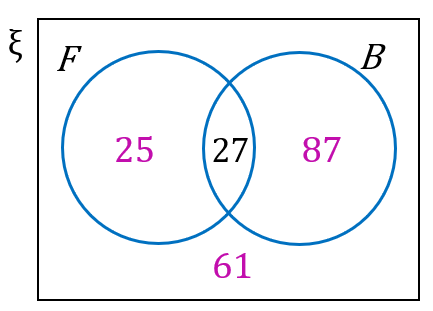
Sebuah kedai buku membuat kajian terhadap 200 orang pelanggan berkaitan dengan pembelian buku fiksyen atau buku bukan fiksyen. Kajian menunjukkan 114 orang membeli buku bukan fiksyen, 52 orang membeli buku fiksyen dan 27 orang membeli kedua-dua buku fiksyen dan bukan fiksyen. Hitung,
(a) bilangan pelanggan yang membeli buku fiksyen sahaja.
(b) bilangan pelanggan yang membeli buku bukan fiksyen sahaja.
(c) bilangan pelanggan yang tidak membeli sebarang buku tersebut.
Penyelesaian:
Katakan F = fiksyen
B = bukan fiksyen
$$ \begin{aligned} & n(\xi)=200 \\ & n(B)=114 \\ & n(F)=52 \\ & n(B \cap F)=27 \end{aligned} $$
(a)
$$ \begin{aligned} n(F \text { sahaja }) & =52-27 \\ & =25 \end{aligned} $$
(b)
$$ \begin{aligned} n(B \text { sahaja }) & =114-27 \\ & =87 \end{aligned} $$
(c)
$$ \begin{aligned} n(F \cup B)^{\prime} & =200-25-27-87 \\ & =61 \end{aligned} $$

Soalan 5:

Murid Tingkatan 4 yang terlibat dalam Program Kitar Semula telah mengumpulkan surat khabar lama, botol plastik dan tin. 72 orang murid mengumpulkan botol plastik, 36 orang murid mengumpulkan surat khabar lama, 25 orang murid mengumpulkan tin, 20 orang murid mengumpulkan surat khabar lama dan botol plastik, 8 orang murid mengumpulkan surat khabar lama dan tin, 18 orang murid mengumpulkan botol plastik dan tin dan 7 orang murid mengumpulkan ketiga-tiga bahan tersebut. Hitung jumlah murid yang terlibat dalam program ini.
Penyelesaian:
Katakan S = surat khabar lama
B = botol plastik
T = tin
$$ \begin{aligned} & n(B)=72 \\ & n(S)=36 \\ & n(T)=25 \\ & n(S \cap B)=20 \\ & n(S \cap T)=8 \\ & n(B \cap T)=18 \\ & n(S \cap B \cap T)=7 \end{aligned} $$
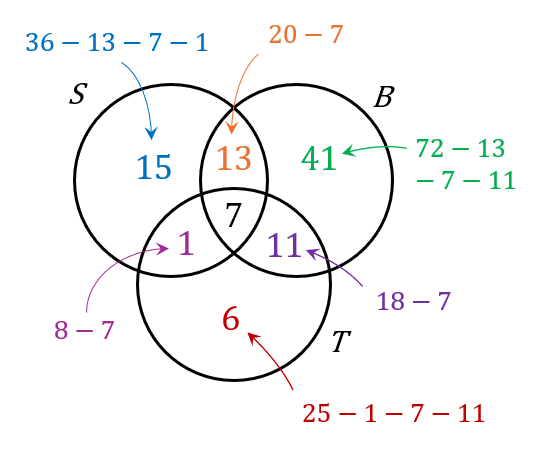
$$ \begin{aligned} n(\xi) & =15+13+41+1+7+11+6 \\ & =94 \text { orang murid } \end{aligned} $$

Murid Tingkatan 4 yang terlibat dalam Program Kitar Semula telah mengumpulkan surat khabar lama, botol plastik dan tin. 72 orang murid mengumpulkan botol plastik, 36 orang murid mengumpulkan surat khabar lama, 25 orang murid mengumpulkan tin, 20 orang murid mengumpulkan surat khabar lama dan botol plastik, 8 orang murid mengumpulkan surat khabar lama dan tin, 18 orang murid mengumpulkan botol plastik dan tin dan 7 orang murid mengumpulkan ketiga-tiga bahan tersebut. Hitung jumlah murid yang terlibat dalam program ini.
Penyelesaian:
Katakan S = surat khabar lama
B = botol plastik
T = tin
$$ \begin{aligned} & n(B)=72 \\ & n(S)=36 \\ & n(T)=25 \\ & n(S \cap B)=20 \\ & n(S \cap T)=8 \\ & n(B \cap T)=18 \\ & n(S \cap B \cap T)=7 \end{aligned} $$

$$ \begin{aligned} n(\xi) & =15+13+41+1+7+11+6 \\ & =94 \text { orang murid } \end{aligned} $$