Soalan 1:
Gambar rajah Venn menunjukkan set semesta ξ, set A dan set B.
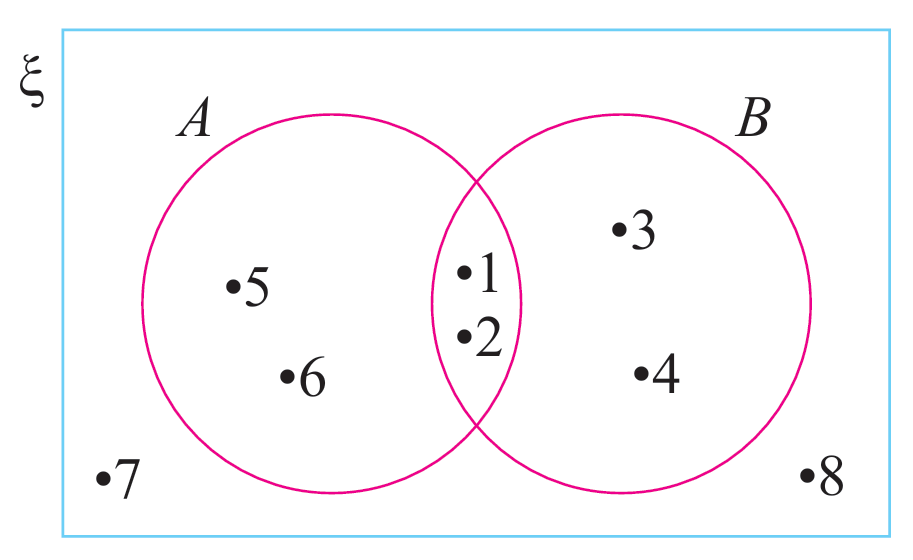 Senaraikan semua unsur bagi set yang berikut.
Senaraikan semua unsur bagi set yang berikut.
(a) A’
(b) B’
(c) (A ∪ B)′
Penyelesaian:
Pelengkap bagi kesatuan set ditulis dengan menggunakan (A ∪ B)’, dibaca sebagai “pelengkap bagi kesatuan set A atau set B”.
Pelengkap bagi kesatuan set A atau set B bermaksud semua unsur yang bukan dalam set A atau set B.
(a)
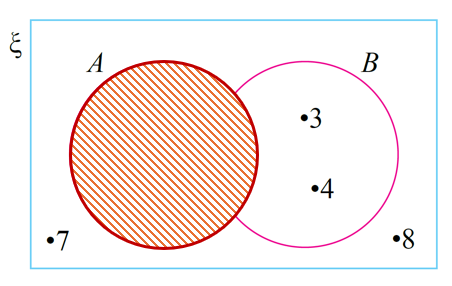
A‘ = {3, 4, 7, 8}
(b)
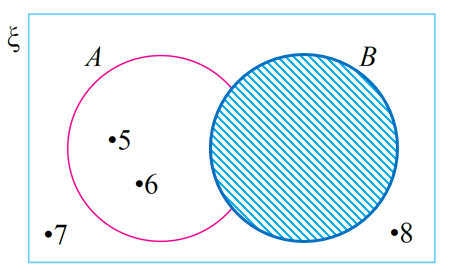
B‘ = {5, 6, 7, 8}
(c)
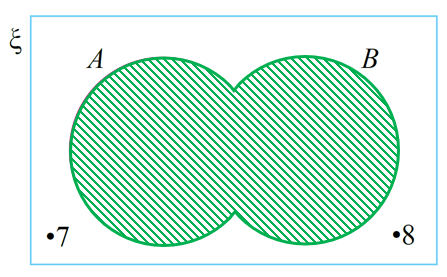
(A∪ B)‘ = {7, 8}
Gambar rajah Venn menunjukkan set semesta ξ, set A dan set B.
 Senaraikan semua unsur bagi set yang berikut.
Senaraikan semua unsur bagi set yang berikut.(a) A’
(b) B’
(c) (A ∪ B)′
Penyelesaian:
Pelengkap bagi kesatuan set ditulis dengan menggunakan (A ∪ B)’, dibaca sebagai “pelengkap bagi kesatuan set A atau set B”.
Pelengkap bagi kesatuan set A atau set B bermaksud semua unsur yang bukan dalam set A atau set B.
(a)

A‘ = {3, 4, 7, 8}
(b)

B‘ = {5, 6, 7, 8}
(c)

(A∪ B)‘ = {7, 8}
Soalan 2:
Diberi ξ = {x : x ialah integer, 10 ≤ x ≤ 30}, set G = {x : x ialah nombor perdana}, set H = {x : x ialah hasil tambah dua digit adalah ganjil} dan set I = {x : x ialah gandaan 6}.
(a) Lukis gambar rajah Venn yang mewakili set semesta ξ , set G, set H dan set I.
(b) Senaraikan semua unsur bagi set yang berikut.
(i) (G ∪ H ) ‘
(ii) ( H ∪ I )′
(iii) ( G ∪ H ∪ I )’
Penyelesaian:
$$ \begin{aligned} \xi & =\{x: x \text { ialah integer, } 10 \leq x \leq 30\} \\ \xi & =\{10,11,12,13,14,15,16,17,18,19,20,21, \\ & 22,23,24,25,26,27,28,29,30\} \end{aligned} $$
$$ \begin{aligned} G & =\{x: x \text { ialah nombor perdana }\} \\ G & =\{11,13,17,19,23,29\} \end{aligned} $$
$$ \begin{aligned} & H=\{x: x \text { ialah hasil tambah dua digit adalah ganjil }\} \\ & H=\{10,12,14,16,18,21,23,25,27,29,30\} \end{aligned} $$
$$ \begin{aligned} & I=\{x: x \text { ialah gandaan } 6\} \\ & I=\{12,18,24,30\} \end{aligned} $$
(a)
$$ \begin{aligned} & G \cap H=\{23,29\} \\ & H \cap I=\{12,18,30\} \\ & G \cap I=\{ \} \\ & G \cap H \cap I=\{ \} \end{aligned} $$
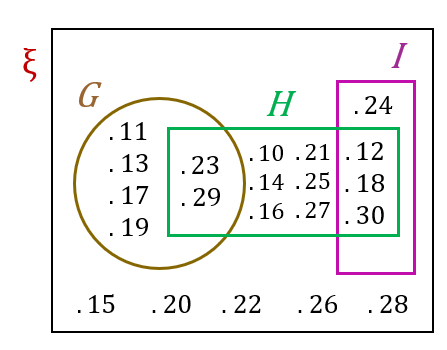
(b)(i)
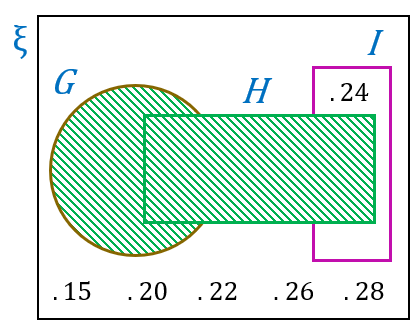
$$ \begin{aligned} & (G \cup H)^{\prime} \\ & =\{15,20,22,24,26,28\} \end{aligned} $$
(b)(ii)
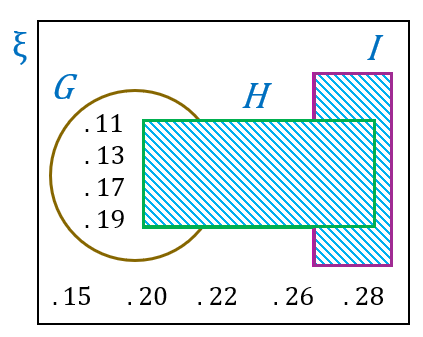
$$ \begin{aligned} & (H \cup I)^{\prime} \\ & =\{11,13,15,17,19,20,22,26,28\} \end{aligned} $$
(b)(iii)
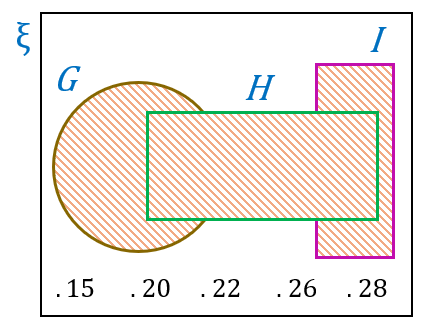
$$ \begin{aligned} & (G \cup H \cup I)^{\prime} \\ & =\{15,20,22,26,28\} \end{aligned} $$
Diberi ξ = {x : x ialah integer, 10 ≤ x ≤ 30}, set G = {x : x ialah nombor perdana}, set H = {x : x ialah hasil tambah dua digit adalah ganjil} dan set I = {x : x ialah gandaan 6}.
(a) Lukis gambar rajah Venn yang mewakili set semesta ξ , set G, set H dan set I.
(b) Senaraikan semua unsur bagi set yang berikut.
(i) (G ∪ H ) ‘
(ii) ( H ∪ I )′
(iii) ( G ∪ H ∪ I )’
Penyelesaian:
$$ \begin{aligned} \xi & =\{x: x \text { ialah integer, } 10 \leq x \leq 30\} \\ \xi & =\{10,11,12,13,14,15,16,17,18,19,20,21, \\ & 22,23,24,25,26,27,28,29,30\} \end{aligned} $$
$$ \begin{aligned} G & =\{x: x \text { ialah nombor perdana }\} \\ G & =\{11,13,17,19,23,29\} \end{aligned} $$
$$ \begin{aligned} & H=\{x: x \text { ialah hasil tambah dua digit adalah ganjil }\} \\ & H=\{10,12,14,16,18,21,23,25,27,29,30\} \end{aligned} $$
$$ \begin{aligned} & I=\{x: x \text { ialah gandaan } 6\} \\ & I=\{12,18,24,30\} \end{aligned} $$
(a)
$$ \begin{aligned} & G \cap H=\{23,29\} \\ & H \cap I=\{12,18,30\} \\ & G \cap I=\{ \} \\ & G \cap H \cap I=\{ \} \end{aligned} $$

(b)(i)

$$ \begin{aligned} & (G \cup H)^{\prime} \\ & =\{15,20,22,24,26,28\} \end{aligned} $$
(b)(ii)

$$ \begin{aligned} & (H \cup I)^{\prime} \\ & =\{11,13,15,17,19,20,22,26,28\} \end{aligned} $$
(b)(iii)

$$ \begin{aligned} & (G \cup H \cup I)^{\prime} \\ & =\{15,20,22,26,28\} \end{aligned} $$
Soalan 3:
Lorekkan kawasan yang mewakili bagi set yang diberikan.
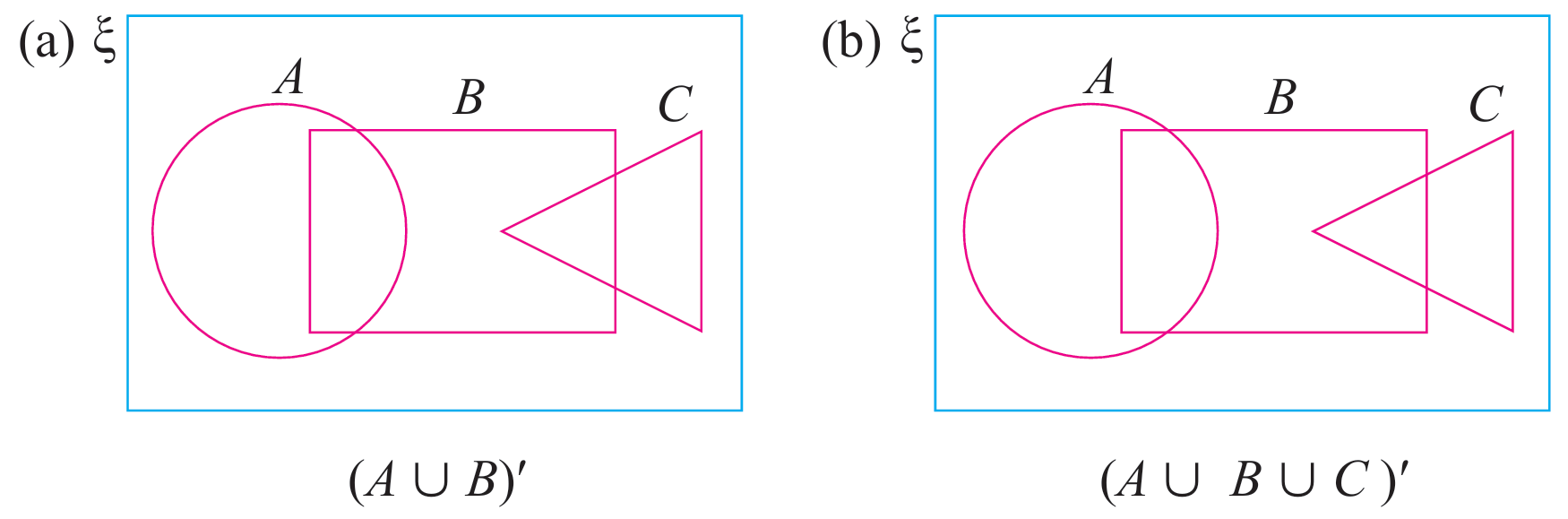
Penyelesaian:
(a)
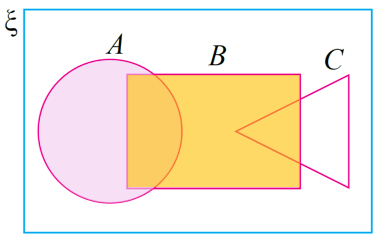
Langkah 1:
Lorekkan kawasan mewakili (A ∪ B)
(b)
Langkah 1:
Lorekkan kawasan mewakili (A ∪ B ∪ C)
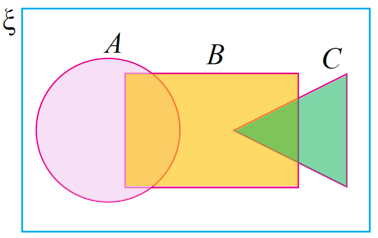
Langkah 2:
Padam kawasan mewakili (A ∪ B ∪ C) dan lorekkan bahagian di luar kawasan (A ∪ B ∪ C) iaitu kawasan (A ∪ B ∪ C)′
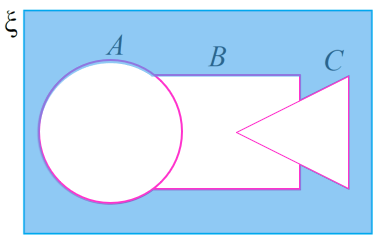
Lorekkan kawasan yang mewakili bagi set yang diberikan.

Penyelesaian:
(a)
Langkah 1:
Lorekkan kawasan mewakili (A ∪ B)

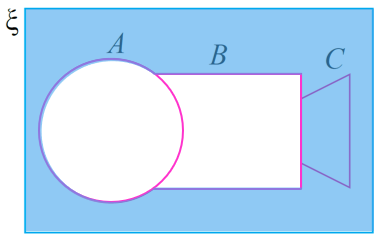
Langkah 2:
Padam kawasan mewakili (A ∪ B) dan lorekkan bahagian di luar kawasan (A ∪ B) iaitu kawasan (A ∪ B)′

(b)
Langkah 1:
Lorekkan kawasan mewakili (A ∪ B ∪ C)

Langkah 2:
Padam kawasan mewakili (A ∪ B ∪ C) dan lorekkan bahagian di luar kawasan (A ∪ B ∪ C) iaitu kawasan (A ∪ B ∪ C)′

Soalan 4:
Lorekkan kawasan yang mewakili bagi set yang diberikan.
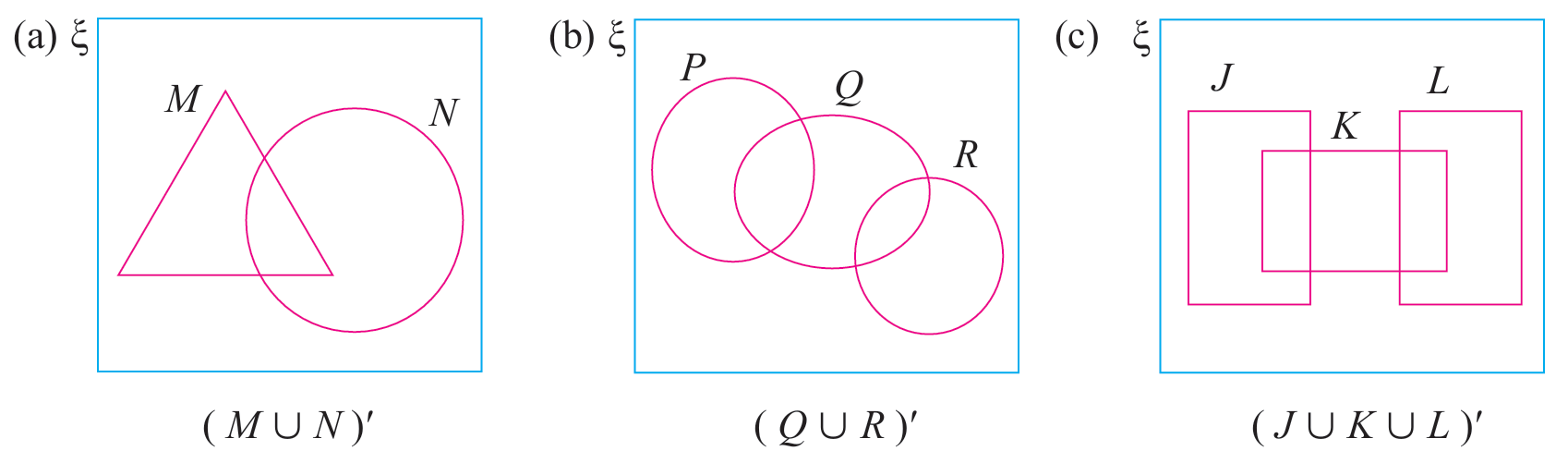
Penyelesaian:
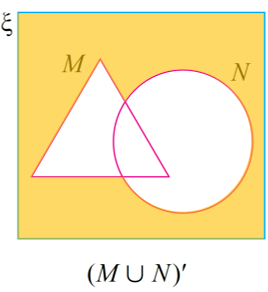
(a)
Lorekkan bahagian di luar kawasan (M ∪ N) iaitu kawasan (M ∪ N)′
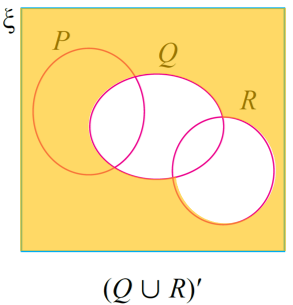
(b)
Lorekkan bahagian di luar kawasan (Q ∪ R) iaitu kawasan (Q ∪ R)′
(c)
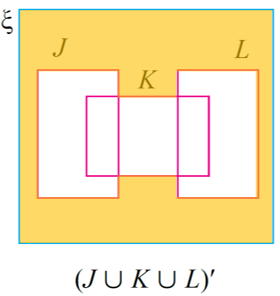
Lorekkan bahagian di luar kawasan (J ∪ K ∪ L) iaitu kawasan (J ∪ K ∪ L)′
Lorekkan kawasan yang mewakili bagi set yang diberikan.

Penyelesaian:
(a)
Lorekkan bahagian di luar kawasan (M ∪ N) iaitu kawasan (M ∪ N)′

(b)
Lorekkan bahagian di luar kawasan (Q ∪ R) iaitu kawasan (Q ∪ R)′

(c)
Lorekkan bahagian di luar kawasan (J ∪ K ∪ L) iaitu kawasan (J ∪ K ∪ L)′
