Soalan 1:
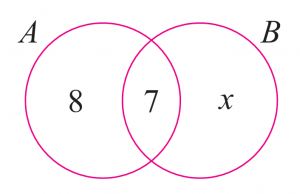
Gambar rajah Venn menunjukkan set A = {ahli Kelab Seni} dan set B = {ahli Kelab Sains}. Jika n(A) = 15 dan n(B) = 22, hitung
(a) nilai x.
(b) jumlah ahli bagi Kelab Seni dan Kelab Sains.
Penyelesaian:
(a)
$$ \begin{aligned} n(B) & =22 \\ 7+x & =22 \\ x & =22-7 \\ x & =15 \end{aligned} $$
(b)
$$ \begin{aligned} \text { Jumlah ahli } & =8+7+x \\ & =8+7+15 \\ & =30 \end{aligned} $$
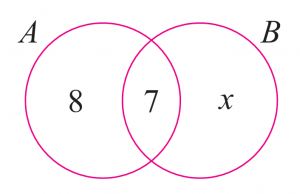
Gambar rajah Venn menunjukkan set A = {ahli Kelab Seni} dan set B = {ahli Kelab Sains}. Jika n(A) = 15 dan n(B) = 22, hitung
(a) nilai x.
(b) jumlah ahli bagi Kelab Seni dan Kelab Sains.
Penyelesaian:
(a)
$$ \begin{aligned} n(B) & =22 \\ 7+x & =22 \\ x & =22-7 \\ x & =15 \end{aligned} $$
(b)
$$ \begin{aligned} \text { Jumlah ahli } & =8+7+x \\ & =8+7+15 \\ & =30 \end{aligned} $$
Soalan 2:
Sebanyak 150 orang murid mengambil ujian diagnostik bagi kedua-dua mata pelajaran Sains dan Matematik. Keputusan menunjukkan sebanyak 40% daripada jumlah murid lulus mata pelajaran Sains dan 30% daripada jumlah murid lulus kedua-dua mata pelajaran tersebut. Jika 8% daripada jumlah murid gagal dalam kedua-dua ujian tersebut, hitung
(a) bilangan murid yang lulus mata pelajaran Matematik.
(b) bilangan murid yang hanya lulus mata pelajaran Sains.
(c) bilangan murid yang hanya lulus mata pelajaran Matematk.
Penyelesaian:
Katakan S = murid yg ambil ujian Sains
M = murid yg ambil ujian Matematik.
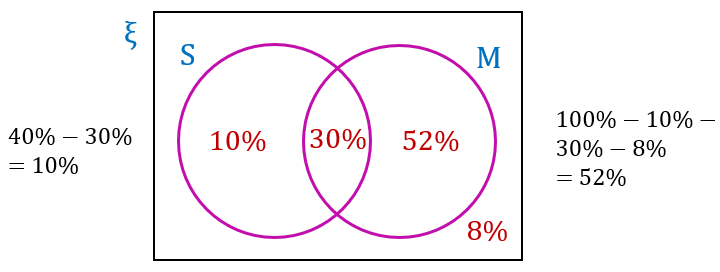
30% daripada jumlah murid lulus kedua-dua mata pelajaran
8% daripada jumlah murid gagal dalam kedua-dua ujian
40% daripada jumlah murid lulus mata pelajaran Sains
(a)
$$ \begin{aligned} &\text { Peratus bilangan murid yang lulus mata pelajaran Matematik }\\ &\begin{aligned} & =30 \%+52 \% \\ & =82 \% \end{aligned} \end{aligned} $$
$$ \begin{aligned} n(M) & =\frac{82}{100} \times 150 \\ & =123 \text { orang murid } \end{aligned} $$
(b)
$$ \begin{aligned} n(\text { hanya lulus mata pelajaran Sains) } & =\frac{10}{100} \times 150 \\ & =15 \text { orang murid } \end{aligned} $$
(c)
$$ \begin{aligned} n(\text { hanya lulus mata pelajaran Matematik) } & =\frac{52}{100} \times 150 \\ & =78 \text { orang murid } \end{aligned} $$
Sebanyak 150 orang murid mengambil ujian diagnostik bagi kedua-dua mata pelajaran Sains dan Matematik. Keputusan menunjukkan sebanyak 40% daripada jumlah murid lulus mata pelajaran Sains dan 30% daripada jumlah murid lulus kedua-dua mata pelajaran tersebut. Jika 8% daripada jumlah murid gagal dalam kedua-dua ujian tersebut, hitung
(a) bilangan murid yang lulus mata pelajaran Matematik.
(b) bilangan murid yang hanya lulus mata pelajaran Sains.
(c) bilangan murid yang hanya lulus mata pelajaran Matematk.
Penyelesaian:
Katakan S = murid yg ambil ujian Sains
M = murid yg ambil ujian Matematik.

30% daripada jumlah murid lulus kedua-dua mata pelajaran
8% daripada jumlah murid gagal dalam kedua-dua ujian
40% daripada jumlah murid lulus mata pelajaran Sains
(a)
$$ \begin{aligned} &\text { Peratus bilangan murid yang lulus mata pelajaran Matematik }\\ &\begin{aligned} & =30 \%+52 \% \\ & =82 \% \end{aligned} \end{aligned} $$
$$ \begin{aligned} n(M) & =\frac{82}{100} \times 150 \\ & =123 \text { orang murid } \end{aligned} $$
(b)
$$ \begin{aligned} n(\text { hanya lulus mata pelajaran Sains) } & =\frac{10}{100} \times 150 \\ & =15 \text { orang murid } \end{aligned} $$
(c)
$$ \begin{aligned} n(\text { hanya lulus mata pelajaran Matematik) } & =\frac{52}{100} \times 150 \\ & =78 \text { orang murid } \end{aligned} $$
Soalan 3:
Sebuah kedai kain mengadakan jualan murah bagi menghabiskan stok kain batik yang berwarna merah, hijau dan biru. Hasil jualan menunjukkan sebanyak 210 orang membeli kain batik tersebut. Jika sebanyak 70 orang membeli kain batik berwarna hijau sahaja, 13 orang membeli kedua-dua kain berwarna hijau dan biru, 50 orang membeli kain batik berwarna biru sahaja dan 15 orang membeli kedua-dua kain batik berwarna hijau dan merah, tidak ada yang membeli ketiga-tiga jenis kain batik tersebut dan tidak ada yang membeli kain berwarna merah dan biru, berapakah bilangan orang yang membeli kain batik berwarna merah sahaja?
Penyelesaian:
Katakan M = orang yang beli batik berwarna merah
H = orang yang beli batik berwarna hijau
B = orang yang beli batik berwarna biru
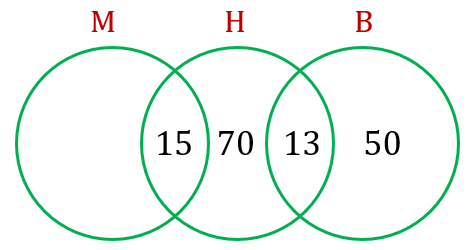
$$ \begin{aligned} & n(\xi)=210 \\ & n(H \text { sahaja })=70 \\ & n(B \text { sahaja })=50 \end{aligned} $$
$$ \begin{aligned} & n(H \cap B)=13 \\ & n(H \cap M)=15 \\ & n(M \cap H \cap B)=0 \\ & n(M \cap B)=0 \end{aligned} $$
$$ \begin{aligned} n(M \text { sahaja }) & =210-15-70-13-50 \\ & =62 \text { orang } \end{aligned} $$
Sebuah kedai kain mengadakan jualan murah bagi menghabiskan stok kain batik yang berwarna merah, hijau dan biru. Hasil jualan menunjukkan sebanyak 210 orang membeli kain batik tersebut. Jika sebanyak 70 orang membeli kain batik berwarna hijau sahaja, 13 orang membeli kedua-dua kain berwarna hijau dan biru, 50 orang membeli kain batik berwarna biru sahaja dan 15 orang membeli kedua-dua kain batik berwarna hijau dan merah, tidak ada yang membeli ketiga-tiga jenis kain batik tersebut dan tidak ada yang membeli kain berwarna merah dan biru, berapakah bilangan orang yang membeli kain batik berwarna merah sahaja?
Penyelesaian:
Katakan M = orang yang beli batik berwarna merah
H = orang yang beli batik berwarna hijau
B = orang yang beli batik berwarna biru

$$ \begin{aligned} & n(\xi)=210 \\ & n(H \text { sahaja })=70 \\ & n(B \text { sahaja })=50 \end{aligned} $$
$$ \begin{aligned} & n(H \cap B)=13 \\ & n(H \cap M)=15 \\ & n(M \cap H \cap B)=0 \\ & n(M \cap B)=0 \end{aligned} $$
$$ \begin{aligned} n(M \text { sahaja }) & =210-15-70-13-50 \\ & =62 \text { orang } \end{aligned} $$
Soalan 4:

Diberi ξ = {murid Tingkatan 4}, set K = {murid yang suka bermain piano} dan set L = {murid yang suka bermain biola}. Jika n(ξ) = 35, n(K) = 15, n(L) = 9 dan n(K ù L) = 5, hitung bilangan murid yang tidak suka bermain kedua-dua alat muzik tersebut.
Penyelesaian:
$$ \begin{aligned} & n(\xi)=35 \\ & n(K)=15 \\ & n(L)=9 \\ & n(K \cap L)=5 \end{aligned} $$
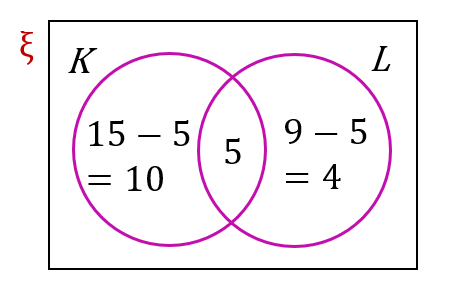 $$
\begin{aligned}
&\text { Bilangan murid yang tidak suka bermain kedua-dua alat muzik }\\
&\begin{aligned}
& =35-10-5-4 \\
& =16
\end{aligned}
\end{aligned}
$$
$$
\begin{aligned}
&\text { Bilangan murid yang tidak suka bermain kedua-dua alat muzik }\\
&\begin{aligned}
& =35-10-5-4 \\
& =16
\end{aligned}
\end{aligned}
$$

Diberi ξ = {murid Tingkatan 4}, set K = {murid yang suka bermain piano} dan set L = {murid yang suka bermain biola}. Jika n(ξ) = 35, n(K) = 15, n(L) = 9 dan n(K ù L) = 5, hitung bilangan murid yang tidak suka bermain kedua-dua alat muzik tersebut.
Penyelesaian:
$$ \begin{aligned} & n(\xi)=35 \\ & n(K)=15 \\ & n(L)=9 \\ & n(K \cap L)=5 \end{aligned} $$
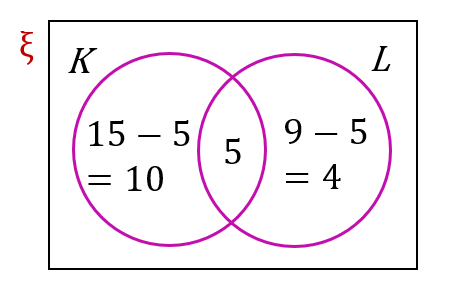 $$
\begin{aligned}
&\text { Bilangan murid yang tidak suka bermain kedua-dua alat muzik }\\
&\begin{aligned}
& =35-10-5-4 \\
& =16
\end{aligned}
\end{aligned}
$$
$$
\begin{aligned}
&\text { Bilangan murid yang tidak suka bermain kedua-dua alat muzik }\\
&\begin{aligned}
& =35-10-5-4 \\
& =16
\end{aligned}
\end{aligned}
$$Soalan 5:
Sebuah Kelab Badminton mengadakan pertandingan badminton antara ahli kelab. Sebanyak 38 orang ahli terlibat dalam acara ini. 20 orang ahli bermain dalam acara beregu dan 26 orang ahli bermain dalam acara perseorangan. Hitung bilangan ahli yang terlibat dalam kedua-dua acara tersebut.

Penyelesaian:
Kaedah I
Bilangan ahli yang terlibat dalam kedua-dua acara
= 20 + 26 – 38
= 8 orang
Kaedah II
Katakan B = ahli bermain dalam acara beregu
P = ahli bermain dalam acara perseorangan
$$ \begin{aligned} & n(\xi)=38 \\ & n(B)=20 \\ & n(P)=26 \\ & n(B \cap P)=x \end{aligned} $$
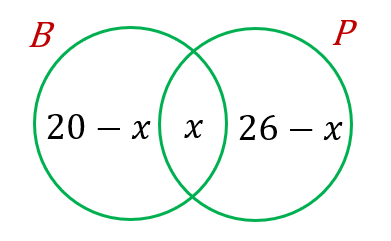
$$ \begin{aligned} (20-x)+x+(26-x) & =38 \\ 46-x & =38 \\ x & =46-38 \\ x & =8 \end{aligned} $$
Sebuah Kelab Badminton mengadakan pertandingan badminton antara ahli kelab. Sebanyak 38 orang ahli terlibat dalam acara ini. 20 orang ahli bermain dalam acara beregu dan 26 orang ahli bermain dalam acara perseorangan. Hitung bilangan ahli yang terlibat dalam kedua-dua acara tersebut.

Penyelesaian:
Kaedah I
Bilangan ahli yang terlibat dalam kedua-dua acara
= 20 + 26 – 38
= 8 orang
Kaedah II
Katakan B = ahli bermain dalam acara beregu
P = ahli bermain dalam acara perseorangan
$$ \begin{aligned} & n(\xi)=38 \\ & n(B)=20 \\ & n(P)=26 \\ & n(B \cap P)=x \end{aligned} $$
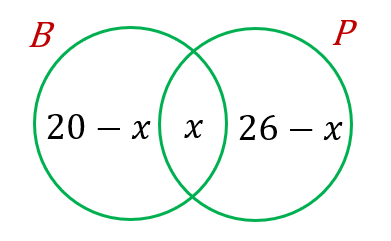
$$ \begin{aligned} (20-x)+x+(26-x) & =38 \\ 46-x & =38 \\ x & =46-38 \\ x & =8 \end{aligned} $$