Soalan 1:
Diberi ξ = {x : x ialah integer, 1 ≤ x ≤ 10}, set M = {x : x ialah nombor ganjil} dan set N = {x : x ialah gandaan 3}. Senaraikan semua unsur bagi set yang berikut.
(a) set M
(b) set N
(c) M ∩ N
Penyelesaian:
Persilangan set wujud apabila terdapat lebih daripada satu set. Persilangan set P dan set Q ditulis menggunakan simbol ∩. P ∩ Q ialah set yang mengandungi unsur-unsur sepunya bagi kedua-dua set P dan set Q.
$$ \begin{aligned} & \xi=\{x: x \text { ialah integer, } 1 \leq x \leq 10\} \\ & \xi=\{1,2,3,4,5,6,7,8,9,10\} \end{aligned} $$
(a)
$$ \begin{aligned} & M=\{x: x \text { ialah nombor ganjil }\} \\ & M=\{1,3,5,7,9\} \end{aligned} $$
(b)
$$ \begin{aligned} N & =\{x: x \text { ialah gandaan } 3\} \\ N & =\{3,6,9\} \end{aligned} $$
(c)
$$ M \cap N=\{3,9\} $$
Diberi ξ = {x : x ialah integer, 1 ≤ x ≤ 10}, set M = {x : x ialah nombor ganjil} dan set N = {x : x ialah gandaan 3}. Senaraikan semua unsur bagi set yang berikut.
(a) set M
(b) set N
(c) M ∩ N
Penyelesaian:
Persilangan set wujud apabila terdapat lebih daripada satu set. Persilangan set P dan set Q ditulis menggunakan simbol ∩. P ∩ Q ialah set yang mengandungi unsur-unsur sepunya bagi kedua-dua set P dan set Q.
$$ \begin{aligned} & \xi=\{x: x \text { ialah integer, } 1 \leq x \leq 10\} \\ & \xi=\{1,2,3,4,5,6,7,8,9,10\} \end{aligned} $$
(a)
$$ \begin{aligned} & M=\{x: x \text { ialah nombor ganjil }\} \\ & M=\{1,3,5,7,9\} \end{aligned} $$
(b)
$$ \begin{aligned} N & =\{x: x \text { ialah gandaan } 3\} \\ N & =\{3,6,9\} \end{aligned} $$
(c)
$$ M \cap N=\{3,9\} $$
Soalan 2:
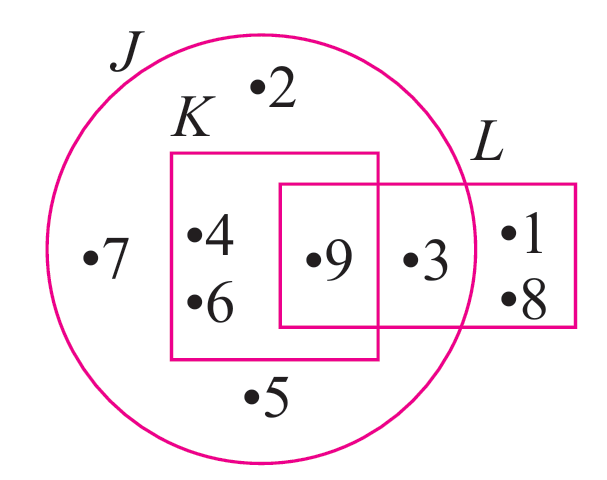
Gambar rajah Venn menunjukkan set J, set K dan set L dengan keadaan set semesta, ξ = {1, 2, 3, 4, 5, 6, 7, 8, 9}. Senaraikan semua unsur bagi persilangan set yang berikut.
(a) J ∩ K
(b) J ∩ L
(c) K ∩ L
(d) J ∩ K ∩ L
Penyelesaian:
(a)
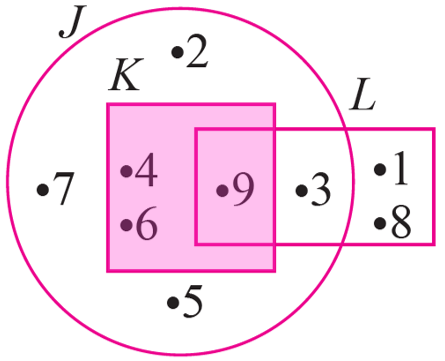
$$ J \cap K=\{4,6,9\} $$
(b)
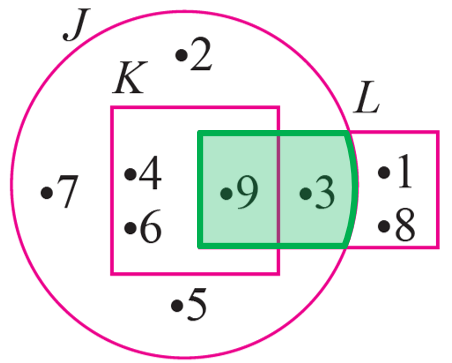
$$ J \cap L=\{3,9\} $$
(c)
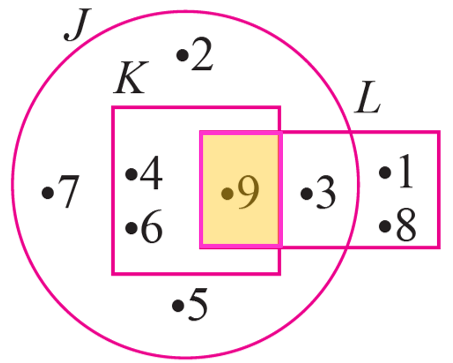
$$ K \cap L=\{9\} $$
(d)
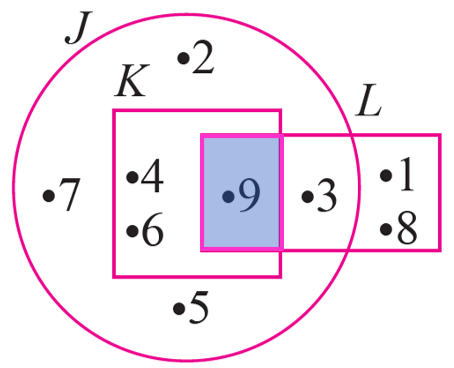
$$ J \cap K \cap L=\{9\} $$

Gambar rajah Venn menunjukkan set J, set K dan set L dengan keadaan set semesta, ξ = {1, 2, 3, 4, 5, 6, 7, 8, 9}. Senaraikan semua unsur bagi persilangan set yang berikut.
(a) J ∩ K
(b) J ∩ L
(c) K ∩ L
(d) J ∩ K ∩ L
Penyelesaian:
(a)

$$ J \cap K=\{4,6,9\} $$
(b)

$$ J \cap L=\{3,9\} $$
(c)

$$ K \cap L=\{9\} $$
(d)

$$ J \cap K \cap L=\{9\} $$
Soalan 3:
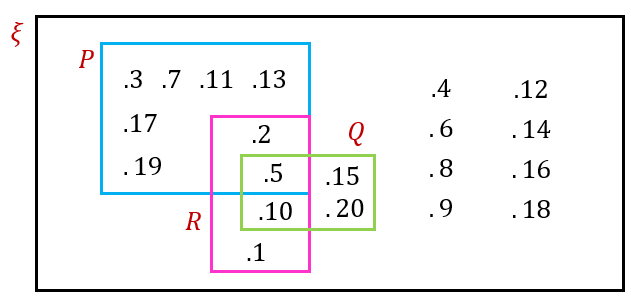
Diberi set semesta, ξ = {x : x ialah integer, 1 ≤ x ≤ 20}, set P = {x : x ialah nombor perdana}, set Q = {x : x ialah gandaan 5} dan set R = {x : x ialah faktor bagi 10},
(a) Lukis gambar rajah Venn mewakilkan semua set yang diberikan.
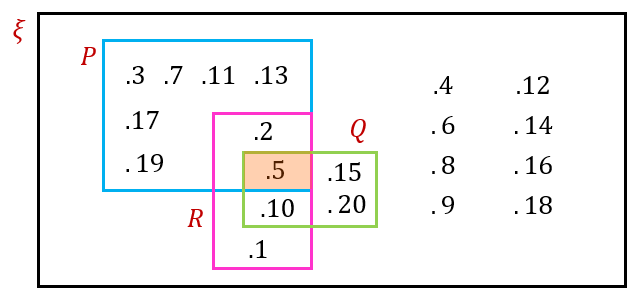
(b) Berdasarkan gambar rajah di (a) lorekkan kawasan mewakili set P ∩ Q ∩ R.
Penyelesaian:
$$ \begin{aligned} & \xi=\{x: x \text { ialah integer, } 1 \leq x \leq 20\} \\ & \xi=\{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20\} \end{aligned} $$
$$ \begin{aligned} & P=\{x: x \text { ialah nombor perdana }\} \\ & P=\{2,3,5,7,11,13,17,19\} \end{aligned} $$
$$ \begin{aligned} Q & =\{x: x \text { ialah gandaan } 5\} \\ Q & =\{5,10,15,20\} \end{aligned} $$
$$ \begin{aligned} & R=\{x: x \text { faktor bagi } 10\} \\ & R=\{1,2,5,10\} \end{aligned} $$
(a)
(b)
P ∩ Q = {5}
P ∩ R = {2, 5}
Q ∩ R = {5, 10}
P ∩ Q ∩ R = {5}
Diberi set semesta, ξ = {x : x ialah integer, 1 ≤ x ≤ 20}, set P = {x : x ialah nombor perdana}, set Q = {x : x ialah gandaan 5} dan set R = {x : x ialah faktor bagi 10},
(a) Lukis gambar rajah Venn mewakilkan semua set yang diberikan.
(b) Berdasarkan gambar rajah di (a) lorekkan kawasan mewakili set P ∩ Q ∩ R.
Penyelesaian:
$$ \begin{aligned} & \xi=\{x: x \text { ialah integer, } 1 \leq x \leq 20\} \\ & \xi=\{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20\} \end{aligned} $$
$$ \begin{aligned} & P=\{x: x \text { ialah nombor perdana }\} \\ & P=\{2,3,5,7,11,13,17,19\} \end{aligned} $$
$$ \begin{aligned} Q & =\{x: x \text { ialah gandaan } 5\} \\ Q & =\{5,10,15,20\} \end{aligned} $$
$$ \begin{aligned} & R=\{x: x \text { faktor bagi } 10\} \\ & R=\{1,2,5,10\} \end{aligned} $$
(a)

(b)
P ∩ Q = {5}
P ∩ R = {2, 5}
Q ∩ R = {5, 10}
P ∩ Q ∩ R = {5}

Soalan 4:
Diberi, set A = {x : x ialah huruf dalam perkataan “GIGIH”}, set B = {x : x ialah huruf dalam perkataan “DEDIKASI”}, dan set C = {x : x ialah huruf dalam perkataan “JUJUR”}, nyatakan bilangan unsur dengan menyenaraikan semua unsur bagi persilangan set yang berikut.
(a) n(A ∩ B)
(b) n(A ∩ C)
(c) n(B ∩ C)
(d) n(A ∩ B ∩ C)
Penyelesaian:
$$ \begin{aligned} & A=\{x: x \text { ialah huruf dalam perkataan “GIGIH” }\} \\ & A=\{\mathrm{G}, \mathrm{I}, \mathrm{H}\} \end{aligned} $$
$$ \begin{aligned} & B=\{x: x \text { ialah huruf dalam perkataan “DEDIKASI” }\} \\ & B=\{\mathrm{D}, \mathrm{E}, \mathrm{I}, \mathrm{~K}, \mathrm{~A}, \mathrm{~S}\} \end{aligned} $$
$$ \begin{aligned} & C=\{x: x \text { ialah huruf dalam perkataan “JUJUR” }\} \\ & C=\{\mathrm{J}, \mathrm{U}, \mathrm{R}\} \end{aligned} $$
(a)
$$ \begin{aligned} & A \cap B=\{I\} \\ & n(A \cap B)=1 \end{aligned} $$
(b)
$$ \begin{aligned} & A \cap C=\{ \} \\ & n(A \cap C)=0 \end{aligned} $$
Set kosong ialah set yang tidak mengandungi sebarang unsur dan boleh diwakili oleh simbol ∅ atau { }.
(c)
$$ \begin{aligned} & B \cap C=\{ \} \\ & n(B \cap C)=0 \end{aligned} $$
(d)
$$ \begin{aligned} & A \cap B \cap C=\emptyset \\ & n(A \cap B \cap C)=0 \end{aligned} $$
Diberi, set A = {x : x ialah huruf dalam perkataan “GIGIH”}, set B = {x : x ialah huruf dalam perkataan “DEDIKASI”}, dan set C = {x : x ialah huruf dalam perkataan “JUJUR”}, nyatakan bilangan unsur dengan menyenaraikan semua unsur bagi persilangan set yang berikut.
(a) n(A ∩ B)
(b) n(A ∩ C)
(c) n(B ∩ C)
(d) n(A ∩ B ∩ C)
Penyelesaian:
$$ \begin{aligned} & A=\{x: x \text { ialah huruf dalam perkataan “GIGIH” }\} \\ & A=\{\mathrm{G}, \mathrm{I}, \mathrm{H}\} \end{aligned} $$
$$ \begin{aligned} & B=\{x: x \text { ialah huruf dalam perkataan “DEDIKASI” }\} \\ & B=\{\mathrm{D}, \mathrm{E}, \mathrm{I}, \mathrm{~K}, \mathrm{~A}, \mathrm{~S}\} \end{aligned} $$
$$ \begin{aligned} & C=\{x: x \text { ialah huruf dalam perkataan “JUJUR” }\} \\ & C=\{\mathrm{J}, \mathrm{U}, \mathrm{R}\} \end{aligned} $$
(a)
$$ \begin{aligned} & A \cap B=\{I\} \\ & n(A \cap B)=1 \end{aligned} $$
(b)
$$ \begin{aligned} & A \cap C=\{ \} \\ & n(A \cap C)=0 \end{aligned} $$
Set kosong ialah set yang tidak mengandungi sebarang unsur dan boleh diwakili oleh simbol ∅ atau { }.
(c)
$$ \begin{aligned} & B \cap C=\{ \} \\ & n(B \cap C)=0 \end{aligned} $$
(d)
$$ \begin{aligned} & A \cap B \cap C=\emptyset \\ & n(A \cap B \cap C)=0 \end{aligned} $$