Praktis Kendiri 2.1c [Soalan 2(a) & (b)] – Buku Teks Matematik Tingkatan 4 Bab 2 (Asas Nombor)

Soalan 2(a):
Hitung nilai bagi setiap operasi tolak yang berikut.
(a) 1111₂ – 10₂

Penyelesaian:
Operasi tolak bagi nombor dalam pelbagai asas

Kaedah 1 : Penukaran Asas
1) Tukar nombor kepada asas sepuluh dan lakukan operasi tolak.

2) Tukarkan semula jawapan dalam asas sepuluh kepada asas dalam soalan.

Kaedah 2 : Bentuk Lazim
1) Tolak digit yang diberikan bermula dari kanan ke kiri.

2) Digit hasil tolak ditulis di ruang jawapan. Hasil tolak sentiasa tidak melebihi asas yang diberikan dan nilainya bersamaan asas sepuluh.

3) Proses ini akan berulang sehingga semua digit dalam nombor selesai ditolak.


(a) 1111₂ – 10₂ (Kaedah 1 : Penukaran Asas)
$$ \begin{aligned} 1111_2 & =\left(1 \times 2^3\right)+\left(1 \times 2^2\right)+\left(1 \times 2^1\right)+\left(1 \times 2^0\right) \\ & =8+4+2+1 \\ & =15_{10} \\ 10_2 & =\left(1 \times 2^1\right)+\left(0 \times 2^0\right) \\ & =2+0 \\ & =2_{10} \\ 15_{10} & =2_{10}=13_{10} \end{aligned} $$
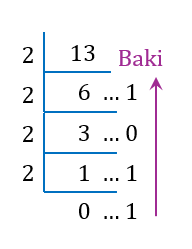$$ \therefore 1111_2-10_2=1011_2 $$


(a) 1111₂ – 10₂ (Kaedah 2 : Bentuk Lazim)
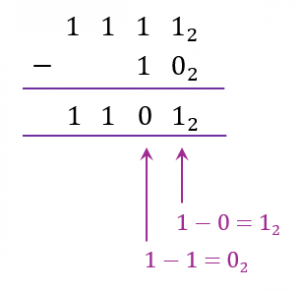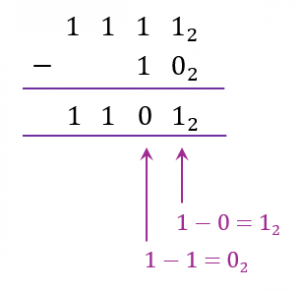$$ \therefore 1111_2-10_2=1011_2 $$

Soalan 2(b):
Hitung nilai bagi setiap operasi tolak yang berikut.
(b) 1011₂ – 101₂

Penyelesaian:
(b) 1011₂ – 101₂ (Kaedah 1 : Penukaran Asas)
$$ \begin{aligned} 1011_2 & =\left(1 \times 2^3\right)+\left(0 \times 2^2\right)+\left(1 \times 2^1\right)+\left(1 \times 2^0\right) \\ & =8+0+2+1 \\ & =11_{10} \\ 101_2 & =\left(1 \times 2^2\right)+\left(0 \times 2^1\right)+\left(1 \times 2^0\right) \\ & =4+0+1 \\ & =5_{10} \\ 11_{10} & -5_{10}=6_{10} \end{aligned} $$
$$ \therefore 1011_2-101_2=110_2 $$


(b) 1011₂ – 101₂ (Kaedah 2 : Bentuk Lazim)

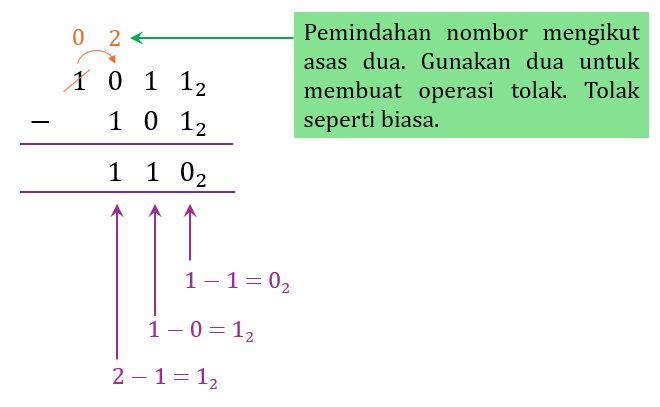$$ \therefore 1011_2-101_2=110_2 $$