Soalan 17(a):
Pertandingan roket air semakin popular di kalangan murid di Malaysia.
(a) Rajah 12 menunjukkan lintasan roket air yang dirakam menggunakan stroboskop apabila dilancarkan pada satah mencancang yang dilukis pada satah Cartes.
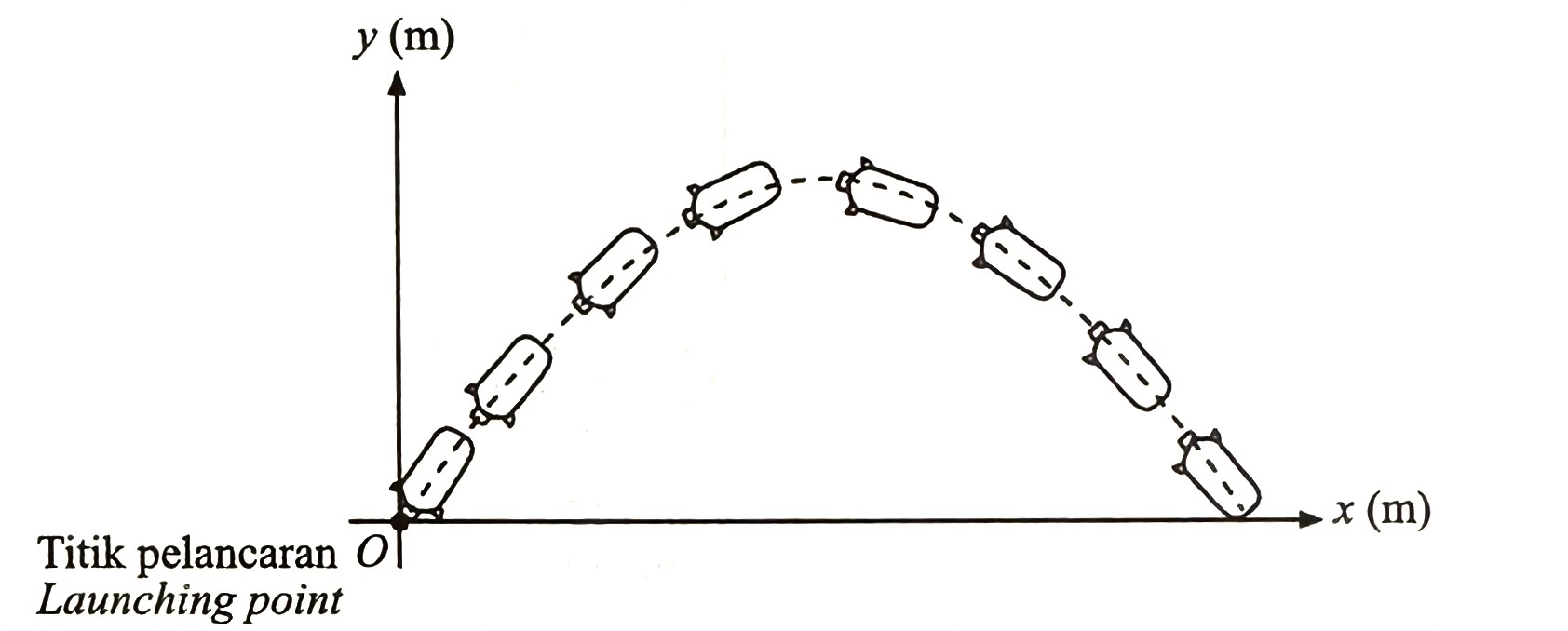
(i) Lintasan roket air itu diwakili oleh fungsi kuadratik, f(x)=ax2 + bx + c. Nyatakan julat nilai a. [1 markah]
(ii) Roket air itu mencapai ketinggian maksimum 5 m dari tanah dan mendarat 8 m dari titik pelancaran. Nyatakan koordinat titik maksimum lintasan roket itu. [2 markah]
Penyelesaian:
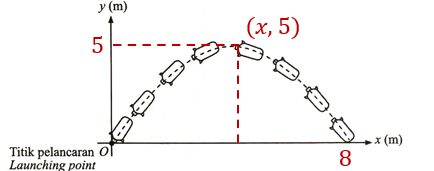
(a)(i) Julat nilai, a < 0
(a)(ii)
$$ \begin{aligned} &\begin{aligned} x & =\frac{0+8}{2} \\ & =4 \end{aligned}\\ &\text { Koordinat titik maksimum }=(4,5) \end{aligned} $$
Pertandingan roket air semakin popular di kalangan murid di Malaysia.
(a) Rajah 12 menunjukkan lintasan roket air yang dirakam menggunakan stroboskop apabila dilancarkan pada satah mencancang yang dilukis pada satah Cartes.

(i) Lintasan roket air itu diwakili oleh fungsi kuadratik, f(x)=ax2 + bx + c. Nyatakan julat nilai a. [1 markah]
(ii) Roket air itu mencapai ketinggian maksimum 5 m dari tanah dan mendarat 8 m dari titik pelancaran. Nyatakan koordinat titik maksimum lintasan roket itu. [2 markah]
Penyelesaian:

(a)(i) Julat nilai, a < 0
(a)(ii)
$$ \begin{aligned} &\begin{aligned} x & =\frac{0+8}{2} \\ & =4 \end{aligned}\\ &\text { Koordinat titik maksimum }=(4,5) \end{aligned} $$
Soalan 17(b):
(b) Jadual 11 menunjukkan kos anggaran bagi penghasilan seunit roket air untuk beberapa pasukan yang bertanding dalam satu karnival STEM.
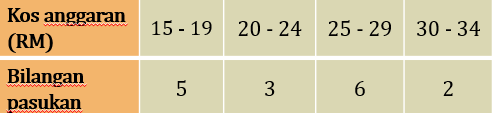
Hitung sisihan piawai bagi data tersebut. [3 markah]
Penyelesaian:
$$ \text { Titik tengah }, x \text { bagi kos anggaran }=\frac{15+19}{2}=17 $$

$$ \begin{aligned} \operatorname{Min}, \bar{x}=\frac{\sum f x}{\Sigma f} & =\frac{5(17)+3(22)+6(27)+2(32)}{5+3+6+2} \\ & =\frac{377}{16} \\ & =23.56 \end{aligned} $$
$$ \begin{aligned} &\text { Sisihan piawai, } \sigma=\sqrt{\frac{\Sigma f x^2}{\Sigma f}-\bar{x}^2}\\ &\begin{aligned} & =\sqrt{\frac{5(17)^2+3(22)^2+6(27)^2+2(32)^2}{16}-23.56^2} \\ & =\sqrt{\frac{9319}{16}-23.56^2} \\ & =5.23 \end{aligned} \end{aligned} $$
(b) Jadual 11 menunjukkan kos anggaran bagi penghasilan seunit roket air untuk beberapa pasukan yang bertanding dalam satu karnival STEM.

Hitung sisihan piawai bagi data tersebut. [3 markah]
Penyelesaian:
$$ \text { Titik tengah }, x \text { bagi kos anggaran }=\frac{15+19}{2}=17 $$

$$ \begin{aligned} \operatorname{Min}, \bar{x}=\frac{\sum f x}{\Sigma f} & =\frac{5(17)+3(22)+6(27)+2(32)}{5+3+6+2} \\ & =\frac{377}{16} \\ & =23.56 \end{aligned} $$
$$ \begin{aligned} &\text { Sisihan piawai, } \sigma=\sqrt{\frac{\Sigma f x^2}{\Sigma f}-\bar{x}^2}\\ &\begin{aligned} & =\sqrt{\frac{5(17)^2+3(22)^2+6(27)^2+2(32)^2}{16}-23.56^2} \\ & =\sqrt{\frac{9319}{16}-23.56^2} \\ & =5.23 \end{aligned} \end{aligned} $$
Soalan 17(c):
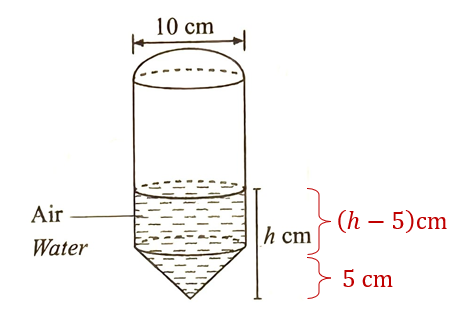
(c) Rajah 13 menunjukkan reka bentuk bagi botol roket air yang terdiri daripada gabungan sebuah hemisfera, sebuah silinder dan sebuah kon. Diberi bahawa ketiga-tiga bentuk ini mempunyai iejari yang sama. Tinggi silinder adalah empat kali jejarinya dan tinggi kon adalah sama dengan jejarinya.
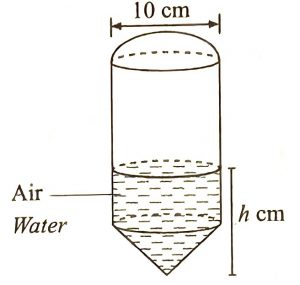
Jika 1/3 daripada isi padu botol roket ini diisi dengan air, hitung nilai h.
[5 markah]
(Guna π = 22/7 )
Penyelesaian:
 $$
\text { Jejari }=\frac{10}{2}=5 \mathrm{~cm}
$$
$$
\text { Jejari }=\frac{10}{2}=5 \mathrm{~cm}
$$
$$ \begin{aligned} &\text { Isi padu hemisfera, }\\ &\begin{aligned} V_1 & =\frac{2}{3} \pi j^3 \\ & =\frac{2}{3} \times \frac{22}{7} \times 5^3 \\ & =\frac{5500}{21} \mathrm{~cm}^3 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Isi padu silinder, } V_2=\pi j^2 h_2\\ &\begin{aligned} & =\frac{22}{7} \times 5^2 \times(4 \times 5) \\ & =\frac{11000}{7} \mathrm{~cm}^3 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Isi padu kon, }\\ &\begin{aligned} V_3 & =\frac{1}{3} \pi j^2 h_3 \\ & =\frac{1}{3} \times \frac{22}{7} \times 5^2 \times 5 \\ & =\frac{2750}{21} \mathrm{~cm}^3 \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Isi padu air } & =\frac{1}{3}\left(\frac{5500}{21}+\frac{11000}{7}+\frac{2750}{21}\right) \\ & =\frac{13750}{21} \mathrm{~cm}^3 \end{aligned} $$
$$ \text { Isi padu air }=\text { isi padu silinder yang diisi dengan air }+ \text { isi padu kon, } V_3 $$
$$ \begin{aligned} \frac{22}{7} \times 5^2 \times(h-5)+\frac{2750}{21} & =\frac{13750}{21} \\ \frac{550}{7} \times(h-5) & =\frac{13750}{21}-\frac{2750}{21} \\ h-5 & =\frac{11000}{21} \times \frac{7}{550} \\ h-5 & =\frac{20}{3} \\ & =11 \frac{2}{3} \mathrm{~cm} \end{aligned} $$
(c) Rajah 13 menunjukkan reka bentuk bagi botol roket air yang terdiri daripada gabungan sebuah hemisfera, sebuah silinder dan sebuah kon. Diberi bahawa ketiga-tiga bentuk ini mempunyai iejari yang sama. Tinggi silinder adalah empat kali jejarinya dan tinggi kon adalah sama dengan jejarinya.

Jika 1/3 daripada isi padu botol roket ini diisi dengan air, hitung nilai h.
[5 markah]
(Guna π = 22/7 )
Penyelesaian:
 $$
\text { Jejari }=\frac{10}{2}=5 \mathrm{~cm}
$$
$$
\text { Jejari }=\frac{10}{2}=5 \mathrm{~cm}
$$$$ \begin{aligned} &\text { Isi padu hemisfera, }\\ &\begin{aligned} V_1 & =\frac{2}{3} \pi j^3 \\ & =\frac{2}{3} \times \frac{22}{7} \times 5^3 \\ & =\frac{5500}{21} \mathrm{~cm}^3 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Isi padu silinder, } V_2=\pi j^2 h_2\\ &\begin{aligned} & =\frac{22}{7} \times 5^2 \times(4 \times 5) \\ & =\frac{11000}{7} \mathrm{~cm}^3 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Isi padu kon, }\\ &\begin{aligned} V_3 & =\frac{1}{3} \pi j^2 h_3 \\ & =\frac{1}{3} \times \frac{22}{7} \times 5^2 \times 5 \\ & =\frac{2750}{21} \mathrm{~cm}^3 \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Isi padu air } & =\frac{1}{3}\left(\frac{5500}{21}+\frac{11000}{7}+\frac{2750}{21}\right) \\ & =\frac{13750}{21} \mathrm{~cm}^3 \end{aligned} $$
$$ \text { Isi padu air }=\text { isi padu silinder yang diisi dengan air }+ \text { isi padu kon, } V_3 $$
$$ \begin{aligned} \frac{22}{7} \times 5^2 \times(h-5)+\frac{2750}{21} & =\frac{13750}{21} \\ \frac{550}{7} \times(h-5) & =\frac{13750}{21}-\frac{2750}{21} \\ h-5 & =\frac{11000}{21} \times \frac{7}{550} \\ h-5 & =\frac{20}{3} \\ & =11 \frac{2}{3} \mathrm{~cm} \end{aligned} $$
Soalan 17(d):
Hubungan antara sudut pelancaran roket air, θ dan jarak pendaratan, l boleh diwakili oleh şuatu rumus trigonometri iaitu $$ l=\frac{u^2}{g}(2 \sin \theta \operatorname{kos} \theta) $$ dengan keadaan u ialah halaju awal roket air dan g ialah pecutan graviti. Seorang murid ingin menentukan sama ada 30∘ atau 45∘ sebagai sudut pelancaran roket airnya supaya roket air mencapai jarak yang lebih jauh.
Penyelesaian:
$$ l=\frac{u^2}{g}(2 \sin \theta \operatorname{kos} \theta) $$
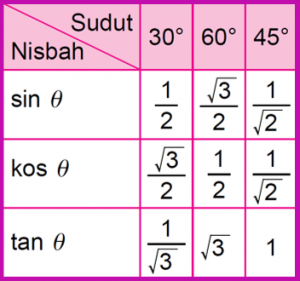
$$ \begin{aligned} l_{30^{\circ}} & =\frac{20^2}{10}\left(2 \sin 30^{\circ} \mathrm{kos} 30^{\circ}\right) \\ & =40\left(2 \times \frac{1}{2} \times \frac{\sqrt{3}}{2}\right) \\ & =20 \sqrt{3} \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} l_{45^{\circ}} & =\frac{20^2}{10}\left(2 \sin 45^{\circ} \operatorname{kos} 45^{\circ}\right) \\ & =40\left(2 \times \frac{1}{\sqrt{2}} \times \frac{1}{\sqrt{2}}\right) \\ & =40 \mathrm{~m} \end{aligned} $$
$$ \therefore \text { Sudut pelancaran terbaik ialah } 45^{\circ} \text {. } $$
Hubungan antara sudut pelancaran roket air, θ dan jarak pendaratan, l boleh diwakili oleh şuatu rumus trigonometri iaitu $$ l=\frac{u^2}{g}(2 \sin \theta \operatorname{kos} \theta) $$ dengan keadaan u ialah halaju awal roket air dan g ialah pecutan graviti. Seorang murid ingin menentukan sama ada 30∘ atau 45∘ sebagai sudut pelancaran roket airnya supaya roket air mencapai jarak yang lebih jauh.
Diberi bahawa u = 20 ms-1 dan g = 10 ms-2. Tanpa menggunakan kalkulator, tentukan sudut pelancaran manakah yang terbaik bagi roket air itu. [4 markah]
Penyelesaian:

$$ l=\frac{u^2}{g}(2 \sin \theta \operatorname{kos} \theta) $$
$$ \begin{aligned} l_{30^{\circ}} & =\frac{20^2}{10}\left(2 \sin 30^{\circ} \mathrm{kos} 30^{\circ}\right) \\ & =40\left(2 \times \frac{1}{2} \times \frac{\sqrt{3}}{2}\right) \\ & =20 \sqrt{3} \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} l_{45^{\circ}} & =\frac{20^2}{10}\left(2 \sin 45^{\circ} \operatorname{kos} 45^{\circ}\right) \\ & =40\left(2 \times \frac{1}{\sqrt{2}} \times \frac{1}{\sqrt{2}}\right) \\ & =40 \mathrm{~m} \end{aligned} $$
$$ \therefore \text { Sudut pelancaran terbaik ialah } 45^{\circ} \text {. } $$