Soalan 16(a):
Sirhan merupakan seorang jurulatih memanah.
(a) Sirhan sedang menyediakan padang bagi aktiviti memanah. Dia ingin membina dua garis berserenjang dengan menggunakan tiga tiang dan tali. Rajah 10 menunjukkan pelan padang memanah dengan tiga tiang P, Q dan R.
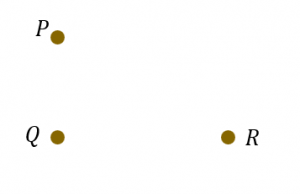Berdasarkan Rajah 10,
(i) namakan bentuk yang terhasil daripada tiga tiang tersebut, [1 markah]
(ii) hitung iarak, dalam m , antara tiang P dan tiang R jika PQ = 2.5 m dan QR = 6.0 m. [2 markah]
Penyelesaian:
(a)(i)
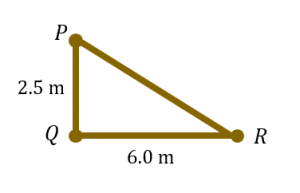Bentuk yang terhasil daripada tiga tiang adalah segi tiga bersudut tegak.
(a)(ii)
$$ \begin{aligned} &\text { Jarak antara tiang } P \text { dan tiang } R\\ &\begin{aligned} & =\sqrt{2.5^2+6^2} \\ & =6.5 \mathrm{~m} \end{aligned} \end{aligned} $$
Sirhan merupakan seorang jurulatih memanah.
(a) Sirhan sedang menyediakan padang bagi aktiviti memanah. Dia ingin membina dua garis berserenjang dengan menggunakan tiga tiang dan tali. Rajah 10 menunjukkan pelan padang memanah dengan tiga tiang P, Q dan R.
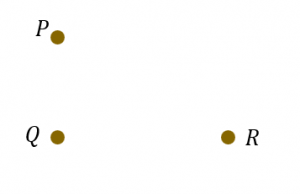Berdasarkan Rajah 10,(i) namakan bentuk yang terhasil daripada tiga tiang tersebut, [1 markah]
(ii) hitung iarak, dalam m , antara tiang P dan tiang R jika PQ = 2.5 m dan QR = 6.0 m. [2 markah]
Penyelesaian:
(a)(i)
Bentuk yang terhasil daripada tiga tiang adalah segi tiga bersudut tegak.(a)(ii)
$$ \begin{aligned} &\text { Jarak antara tiang } P \text { dan tiang } R\\ &\begin{aligned} & =\sqrt{2.5^2+6^2} \\ & =6.5 \mathrm{~m} \end{aligned} \end{aligned} $$
Soalan 16(b):
$$ \begin{aligned} P(z) & =\frac{3}{5} \\ P\left(z^{\prime}\right) & =1-\frac{3}{5} \\ & =\frac{2}{5} \end{aligned} $$
$$ \begin{aligned} P(s) & =\frac{4}{9} \\ P\left(s^{\prime}\right) & =1-\frac{4}{9} \\ & =\frac{5}{9} \end{aligned} $$
$$ \begin{aligned} & P \text { (Zarif atau Syafi melangkah ke pusingan kedua) } \\ & =1-P(\text { Kedua-dua Zarif dan Syafi tidak melangkah ke } \\ & \quad \text { pusingan kedua) } \\ & =1-P\left(z^{\prime}\right) P\left(s^{\prime}\right) \\ & =1-\left(\frac{2}{5} \times \frac{5}{9}\right) \\ & =\frac{7}{9} \end{aligned} $$
(b) Dua orang pelatih Sirhan iaitu Zarif dan Syafi sedang bertanding di pusingan awal suatu pertandingan memanah. Diberi bahawa kebarangkalian Zarif melangkah ke pusingan kedua ialah 3/5 dan kebarangkalian Syafi melangkah ke pusingan kedua ialah 4/9.
Cari kebarangkalian bahawa Zarif atau Syafi melangkah ke pusingan kedua pertandingan itu.
[3 markah]
$$ \begin{aligned} P(z) & =\frac{3}{5} \\ P\left(z^{\prime}\right) & =1-\frac{3}{5} \\ & =\frac{2}{5} \end{aligned} $$
$$ \begin{aligned} P(s) & =\frac{4}{9} \\ P\left(s^{\prime}\right) & =1-\frac{4}{9} \\ & =\frac{5}{9} \end{aligned} $$
$$ \begin{aligned} & P \text { (Zarif atau Syafi melangkah ke pusingan kedua) } \\ & =1-P(\text { Kedua-dua Zarif dan Syafi tidak melangkah ke } \\ & \quad \text { pusingan kedua) } \\ & =1-P\left(z^{\prime}\right) P\left(s^{\prime}\right) \\ & =1-\left(\frac{2}{5} \times \frac{5}{9}\right) \\ & =\frac{7}{9} \end{aligned} $$
Soalan 16(c):
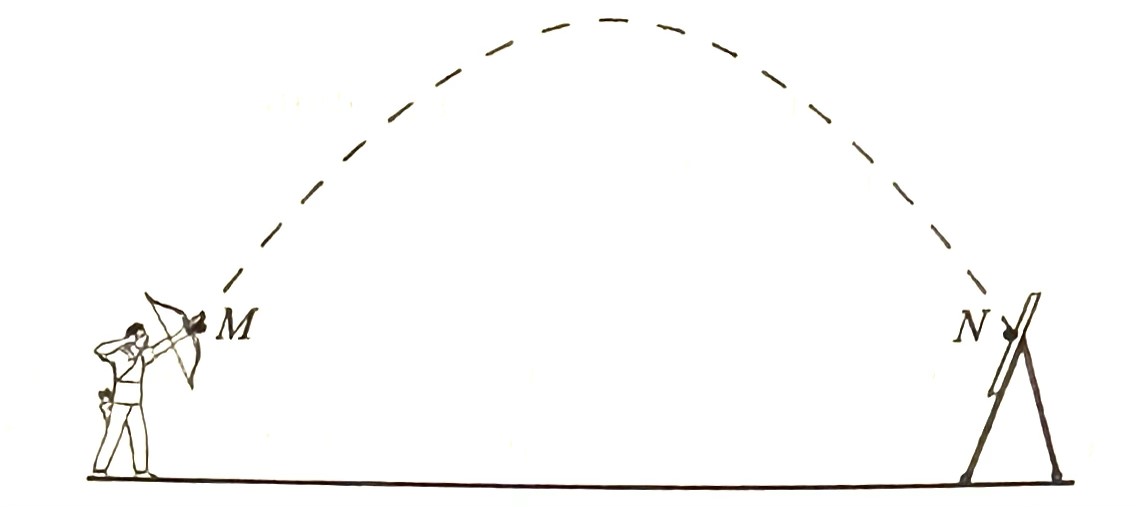
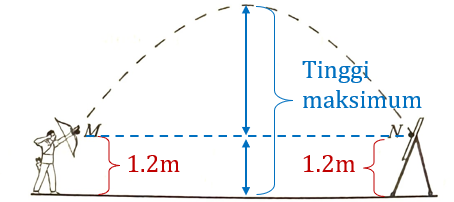
(c) Seorang budak lelaki telah melakukan panahan. Rajah 11 menuniukkan lintasan anak panah itu dari titik M ke titik N.
Penyelesaian:
$$
f(x)=-\frac{13}{200} x^2+\frac{39}{20} x
$$
$$ \begin{aligned} x & =-\frac{b}{2 a} \\ & =-\frac{\left(\frac{39}{20}\right)}{2\left(-\frac{13}{200}\right)} \\ & =-\frac{39}{20} \times-\frac{100}{13} \\ & =15 \end{aligned} $$
$$ \begin{aligned} f(15) & =-\frac{13}{200}(15)^2+\frac{39}{20}(15) \\ & =14.625 \end{aligned} $$
$$ \begin{aligned} \text { Tinggi maksimum } & =14.625 \mathrm{~m}+1.2 \mathrm{~m} \\ & =15.825 \mathrm{~m} \end{aligned} $$
(c) Seorang budak lelaki telah melakukan panahan. Rajah 11 menuniukkan lintasan anak panah itu dari titik M ke titik N.
Titik M dan titik N berada 1.2 m tegak di atas tanah mengufuk. Lintasan anak panah dapat diwakili oleh fungsi kuadratik, $$
f(x)=\frac{13}{200} x^2+\frac{39}{20} x
$$
Hitung tinggi maksimum, dalam m, yang dicapai oleh anak panah yang diukur dari permukaan tanah. [5 markah]
Penyelesaian:
$$
f(x)=-\frac{13}{200} x^2+\frac{39}{20} x
$$$$ \begin{aligned} x & =-\frac{b}{2 a} \\ & =-\frac{\left(\frac{39}{20}\right)}{2\left(-\frac{13}{200}\right)} \\ & =-\frac{39}{20} \times-\frac{100}{13} \\ & =15 \end{aligned} $$
$$ \begin{aligned} f(15) & =-\frac{13}{200}(15)^2+\frac{39}{20}(15) \\ & =14.625 \end{aligned} $$
$$ \begin{aligned} \text { Tinggi maksimum } & =14.625 \mathrm{~m}+1.2 \mathrm{~m} \\ & =15.825 \mathrm{~m} \end{aligned} $$
Soalan 16(d):
Sirhan merekodkan skor bagi Zarif dan skor bagi Syafi. Dia menghitung min dan sisihan piawai bagi skor Zarif iaitu masing-masing adalah 7.542 dan 1.233. Iadual 10 menunjukkan taburan skor bagi Syafi.
Dengan menghitung min dan sisihan piawai bagi skor Syafi, bandingkan prestasi keduadua pemanah itu. Anda hendaklah memberi komen tentang pemanah manakah yang menunjukkan prestasi yang lebih baik secara purata dan pemanah manakah lebih konsisten.
[4 markah]
Penyelesaian:
$$ \begin{aligned} \text { Min, } \bar{x} \text { bagi Syafi } & =\frac{\sum f x}{\Sigma f} \\ & =\frac{19(6)+21(7)+24(8)+6(9)+2(10)}{19+21+24+6+2} \\ & =\frac{527}{72} \\ & =7.319 \end{aligned} $$
Min bagi Zarif ialah 7.542, maka Zarif menunjukkan prestasi yang lebih baik secara purata.
$$ \begin{aligned} & \text { Sisihan piawai bagi Syafi }=\sqrt{\frac{\Sigma f x^2}{\Sigma f}-\bar{x}^2} \\ & \begin{aligned} \sigma & =\sqrt{\frac{19(6)^2+21(7)^2+24(8)^2+6(9)^2+2(10)^2}{72}-7.319^2} \\ & =\sqrt{\frac{3935}{72}-7.319^2} \\ & =1.042 \end{aligned} \end{aligned} $$
$$ \text { Sisihan piawai bagi Zarif ialah 1.233. Dalam hal ini, Syafi lebih konsisten. } $$
Sirhan merekodkan skor bagi Zarif dan skor bagi Syafi. Dia menghitung min dan sisihan piawai bagi skor Zarif iaitu masing-masing adalah 7.542 dan 1.233. Iadual 10 menunjukkan taburan skor bagi Syafi.
Dengan menghitung min dan sisihan piawai bagi skor Syafi, bandingkan prestasi keduadua pemanah itu. Anda hendaklah memberi komen tentang pemanah manakah yang menunjukkan prestasi yang lebih baik secara purata dan pemanah manakah lebih konsisten.
[4 markah]
Penyelesaian:
$$ \begin{aligned} \text { Min, } \bar{x} \text { bagi Syafi } & =\frac{\sum f x}{\Sigma f} \\ & =\frac{19(6)+21(7)+24(8)+6(9)+2(10)}{19+21+24+6+2} \\ & =\frac{527}{72} \\ & =7.319 \end{aligned} $$
Min bagi Zarif ialah 7.542, maka Zarif menunjukkan prestasi yang lebih baik secara purata.
$$ \begin{aligned} & \text { Sisihan piawai bagi Syafi }=\sqrt{\frac{\Sigma f x^2}{\Sigma f}-\bar{x}^2} \\ & \begin{aligned} \sigma & =\sqrt{\frac{19(6)^2+21(7)^2+24(8)^2+6(9)^2+2(10)^2}{72}-7.319^2} \\ & =\sqrt{\frac{3935}{72}-7.319^2} \\ & =1.042 \end{aligned} \end{aligned} $$
$$ \text { Sisihan piawai bagi Zarif ialah 1.233. Dalam hal ini, Syafi lebih konsisten. } $$